基于多媒體技術的數學實驗的教學價值

　　數學實驗是指根據教學目標，充分利用實驗手段尤其是運用現代教育技術，創設一定的教學情境，通過思考和操作活動，研究數學現象的本質和發現數學規律，讓學生親身體驗數學知識的建構過程，這是一種思維實驗和操作實驗相結合的實驗。實驗能直接刺激大腦進行積極思維，可以幫助人們獲取感性認識并使人們的感性認識上升為理性認識。
　　多媒體技術使數學的實驗手段豐富起來，計算機的計算、圖形、圖像及動畫等功能，能為抽象思維提供直觀模型，使數學關系的靜態結構表現為時空中的動態過程，將一個數學問題發生與解決的全過程展現在人們的面前。
　　
　　一、促進概念形成
　　
　　傳統的數學概念教學幾乎沒有數學實驗，學生的活動機會不多。除了教學觀念制約，在教學中難于開展數學實驗的一個重要原因是技術條件的限制。例如，研究一個數列，在很短時間內不可能計算出它的任意幾項；研究函數的性質，不可能在同一坐標系中準確迅速畫出幾個函數圖像加以比較，得出函數性質。現在有了計算機，這一切都已成為可能，從而增加了學生的活動機會，改變了數學概念教學的方法。
　　例如，數列極限是數學概念教學的一個難點， 在過去的教學中很難把隨ｎ的不斷變化而趨向某個常數或不趨向于某個常數的動態過程顯露出來，更不能提供一個學生參與的認知環境。
　　我們開發的軟件在這方面做了有益的嘗試，第一部分以列表、描點等多種方式顯示了an無限趨向于A的過程。第二部分通過典型分析法抽象出“ε—N”的定義。給出某一具體數列后，屏幕上首先顯示出此數列前10項的值，稍后在數軸上描出表示這10項的點。接下來提示學生做下面的實驗：“請鍵入你認為十分小的正數ε并觀察相應的N值并計算an以后的5項與A的誤差。” 學生自由地做實驗，直到他們認可了對于無論事先給定的多么小的正數ε，總存在N，當n＞N時，都有│an－A│＜ε。學生通過自己鍵入n值觀察an的變化趨勢，把數列的通項隨ｎ變化的動態過程顯示出來，反復體驗何謂“無限逼近”，從而真正領悟到抽象的極限概念。
　　
　　二、給學生發現的機會
　　
　　多媒體技術在數學教學中的運用，給學生以“數學發現”的機會。這種教學體現了用實驗手段和歸納方法進行數學教學的思想：從若干實例出發→在計算機上做大量的實驗→發現規律→提出猜想→理性證明，體現了教學過程中教師、學生、內容、媒體四要素功能的轉變。
　　例如，圓周角與同弧上的圓心角有什么關系？同弧上圓內角、圓外角與圓周角有什么關系？兩條相交弦的夾角與它所對的弧有什么關系？首先可用幾何畫板畫出圖形，度量你要觀察的量，然后比較它們的數量關系。圖1是一個研究圓周角性質的動畫實驗室，學生只需拖動有關點或點擊動畫按鈕，屏幕便出現動畫效果。同時，弧、圓心角與圓周角的度數也及時測量并顯示出來。你一定會有“我發現了”的感受。
　　
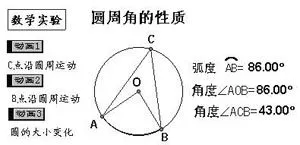
　　　　圖1
　　
　　實驗是發現真理的一條有效途徑。數學是建立在推理的基礎上的，只有經過理性證明，發現的結果才能真正成為定理（公式）。教師在學生實驗觀察之后，可組織他們交流并引導他們對觀察結果做出證明。
　　三、架設數形結合的橋梁
　　數形結合是一種非常重要的數學思想。在數學發展過程中，數與形常常結合在一起，內容上互相聯系，方法上互相滲透，并在一定的條件下互相轉化。運用數形結合思想，可使數與形各展其長，使邏輯思維與形象思維完美地統一起來，將復雜問題簡單化，抽象問題具體化。計算機為我們提供了數形結合的手段。例如，利用幾何畫板畫圖后，馬上就可以測算出數值，并能把圖形變化過程中的數量關系的變化（哪怕是微小的變化）直觀地顯示出來。數與形的變化同時進行，為數學的學習提供了絕好的實驗工具，這在傳統數學教學中根本無法辦到，幾何畫板是幫助學生學通數學的有效工具。
　　例如，利用計算機做下列數學實驗，學生一人一 機，機內裝有顯示一般正弦函數y=Asin(ωx+φ)的圖像的應用軟件（操作界面見圖2）。啟動該軟件后，學生可用鼠標任意改變畫面中的點C、點J、點F的位置，亦即改變參數A、ω、φ的值，使圖像產生相應的變化。學生手、眼、腦并用，通過考察函數式y=Asin(ωx+φ)中三個參數A、ω、φ對函數圖像的影響，對圖像的振幅變換、周期變換、相位變換產生感性認識。整個過程直觀、形象，充分顯現數與形相互依賴的變化過程，對于學生更好地理解和掌握正弦函數的圖像和性質，從理論上探究相關的數學規律打下堅實的基礎。
　　
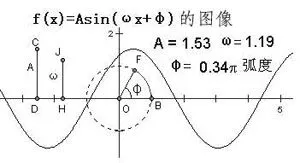
　　　　圖2
　　
　　計算機強大的圖形、圖像功能，把“數”與“形”緊緊結合在一起，使抽象的數學變得形象、生動、有趣。
　　
　　四、改變數學教學模式
　　
　　引進數學實驗以后，數學教學可以應用一種新的模式，即“問題—實驗—交流—練習—回顧”。首先提出有吸引力的數學問題，利用計算機創設的動態情境，引導學生在多媒體技術的支持下做數學實驗。實驗時可把學生分成2～3人一組，每組共用一臺計算機。讓學生自主地進行探索、分析和思考。學生在實驗情境中“做”數學，對知識的形成過程，對問題發現、解決、引申、變換等過程的實驗模擬和探索，可激發學習動機，有助于深刻理解知識，有助于形成證明的基礎平臺和對邏輯演繹證明的本質把握。這種實驗式的教和學拓寬了學生的思維活動空間，使他們的思維更有深刻性和批判性。在實驗的基礎上組織學生小組討論或全班交流，在交流過程中，教師及時的插話、生動的演講可融入其中。這樣既可以發揮傳統教學的優勢，又可以在集體的環境中集中大家的意見，組織不同觀點的交鋒。傳統教學中教師對問題的深刻闡述、機智的解題策略、對學生各種常見錯誤認識的分析、對數學美的詮釋等等，并沒有被數學實驗所替代，只是在交流的過程中，這些才成為學生的真正需要。實驗與交流結合起來凸顯了數學知識的形成過程，而練習與回顧對鞏固和強化數學知識同樣是必要的，練習應面對所有不同水平的學生，應能及時提供反饋和幫助，并能及時對每一個學生做出科學的評估。
　　
　　參考文獻
　　[1]俞瑞康主編.師范課堂教學模式[M]. 上海：百家出版社. 2001.
　　[2]陶維林.幾何畫板實用范例教程[M].北京：清華大學出版社.2001.
　　（作者單位：江蘇無錫高等師范學