日出江淮紅勝火，春來江水綠如藍

　　1立足雙基。 試題平穩重基礎，清新雋永，頗具內涵，無怪題和偏題。
　　
　　選擇題起點低、坡度緩，除第11、12題比較靈活外，其他題幾乎是一馬平川，有利于學生及早進入狀態，增強自信心，這是區別于往年考題的一個顯著特點。 填空題比選擇題稍難，運算量增大，除第16題比較靈活外，其他仍然是考生熟悉的常規題型。 解答題的前三題都屬基礎題，其難度與教材的習題難度相當，并且有幾道題與課本的習題有關，如第(4)題是由高二數學(上)第11頁習題第1題引申得到，第(9)題是由高二數學(下)第74頁練習第3題改編得到等，這些題雖源于課本，但又高于課本，這對中學數學教學有很好的導向作用。 縱觀試題，個個皆“樸素”，既無高深的知識，又無生僻的技巧。 許多題取材于課本的例、習題的變式題或引申題，利用學生熟悉的知識、問題、及情景做原型，考查三基。 如理科第(1)——(7)、(10)、(13)、(14)、(17)、(18)、(19)、(21)Ⅱ題等，其中第(1)、(5)題是對單一知識點的考查，(5)兼有分類討論的思想方法；第(2)、(3)、(7)、(10)、(12)、(13)、(14)、(17)、(18)、題用基本的公式、方法均可完成；(4)、(6)、(11)既可直接求解，也可用演繹法——特殊和一般的關系(如特值法)；第(4)題的不必要性，只要令a=1，b=0即可；第(6)題采取驗證法較易。 試卷引導我們在教學中跨出題海，真正回到重視基礎的軌道。 看看今年考生考完數學的笑臉，你就明白2006年高考復習的起點高了，資料偏難，訓練過繁過量。 誠然，我們要正確理解這里的“基礎”，它不是指應對考試的基礎，即機械重復訓練的常規題目，而是指體驗知識的形成過程以及對知識本質的頓悟。 對高考試卷分析表明，考生答題失誤，并不是因為缺乏靈活的思維和敏銳的感覺，而恰恰因為基礎知識、基本理論的掌握上存在缺陷。 因此，2007年的高考復習，必須回歸基礎，不僅弄懂課本提供的知識和方法，還要弄懂數學定理和公式的推導過程，如理科(20)題用到等比數列求和過程中的“錯位相減法”及分類討論的思想，對習題多作一些推廣和變式練習，以揭示知識與方法的聯系。 一言敝之，對知識不僅要“廣積糧”還要“深挖洞”，既要求全面但更重要是求聯系。
　　
　　2突出主干知識的考查。
　　
　　試題對教材各章內容都有所涉及，重點考查高中數學知識的主干內容，如：函數、三角函數、數列、直線與平面、圓錐曲線、概率這六大主干知識，并保持比較高的比例和必要的深度。 如函數約占27分，數列約占12分，三角函數約占27分，概率占17分，立體幾何占21分，解析幾何占27分，總計約131分。 鑒于此，2007年的備考要以熟練掌握主干知識為龍頭，立足于通性、通法的訓練，歸宿于數學思想和方法的強化。
　　重視主干知識的形成，必然要理清主干知識的脈絡，分析主干知識的內涵、外延和交匯。 充分重視主干知識的支撐作用，以主干知識為支柱，構建知識網絡。 如在函數的復習中一定要鏈接導數，在向量的復習中要融入平面幾何、立體幾何、解析幾何、三角函數和數列，不等式的復習中傾注函數、數列、向量和解析幾何，排列、組合與概率和概率統計二合一為一章進行復習等等。 如此這般漸漸模糊知識模塊和章節的界限，最后達到交匯統一。
　　
　　3加大新舊知識整合的力度。
　　
　　向量、概率、導數等新增內容工具性強，應用廣泛，它們的引入給傳統內容注入了新的活力。 體現新舊內容的結合，突出使用新觀點、新方法來解決傳統問題，在知識的交匯處設計試題是高考題的一大特點：如第(2)題集合、不等式、函數的相濡以沫；第(4)題不等式與簡易邏輯的滲透；第(7)題是曲線的切線與導數幾何意義的結合；第(10)題的線性規劃與幾何的牽手；第(12)題的立體幾何與排列組合、概率的不期而遇；第(18)題是概率與應用題的聯袂；第(19)題為立體幾何與向量的姻緣；第(20)題是抽象函數、分段函數、函數性質的交匯；第(21)題為數列與函數導數的狹路相逢；第(22)題直線與雙曲線、平面幾何的群英薈萃，都是知識交匯的經典之作。 試題在向量、概率、導數、線性規劃等新增內容突出了對導數與相關知識交匯考查的力度，削弱了對向量的考查。 體現導數的工具性，更強調導數與其他知識間的聯系。 導數的工具性考查力度有余，向量的綜合性整合幅度明顯不足。 第(19)題立體幾何解答題仍采用“一題兩法”的命題辦法，顯然研究垂直、夾角等問題向量法更易上手。
　　
　　4深化能力立意，突出數學思想方法的考查。
　　
　　如理科的第(2)、(6)、(8)、(9)、(11)、(16)、(20)、(21)題是對思維能力中的直覺猜想能力的考查；第(3)、(12)、(14)、(16)、(19)考查了空間想象能力，主要體現在對文字語言、符號語言和圖形語言的互相轉化，以及對圖形的識別、理解和加工，與運算能力、邏輯思維能力相結合；理科第(21)題是對思維能力的模式構建能力的考查；第(15)、(21)題是對思維能力中的歸納想象、演繹證明能力的考查等等。
　　對數學思想和方法的考查主要涉及數形結合的思想方法，如理科的(6)、(7)、(10)、(19)、(22)等；轉化與化歸的思想方法如(4)、(6)、(9)、(11)、(12)、(20)等；如(9)題是球內接正八面體的問題，學生不熟悉此情景，但由對稱性可知：即為棱長相等的正四棱錐內接于半球的問題，從而化歸為較熟悉的正四棱錐的問題；分類討論的思想方法如理科(5)、(16)、(18)、(20)題等；函數與方程的思想方法如(13)、(17)、(20)、(21)、(22)等；又(20)、(21)、(22)分別考查了換元法、數學歸納法、待定系數法、錯位相減法、導數法等。 這些思想方法是平時教學中反復應用和錘煉的，也是學生耳熱能詳的，關鍵在考場上能否抓住本質，應用恰當的思想方法，以簡捷、明快的思維發現解決問題的途徑。
　　2007年備考中應重視數學基本思想方法的滲透和應用。 尤其要重視配方法、換元法、待定系數法、數學歸納法和數形結合法等常用數學技能和方法；分析法、綜合法、歸納法、演繹法和反證法等常用的邏輯推理方法；函數與方程、變換與轉化、分類與歸納、數形的結合與分離、定常與變化的對立和統一等重要的數學思想和方法。 以夯實主干知識為原點，以熟練數學思想方法為支點，以提升能力為駐點，不遺余力地培養學生較高的思維層次中的探索能力、直覺思維能力、合情推理能力、創新能力。
　　
　　5出題思路靈活多變，試題形式多樣。
　　
　　試卷注意用學生熟悉的、常見的背景，重新設計考查數學思想方法、數學思維品質的試題，跳出平時的模擬試題和復習資料上的題目，試題背景設計公平，貼近學生實際，問題設計入口寬、層次清、方法多，使不同的學生都能在公平的背景下展示真實的水平。如(11)、(12)是知識載體創新，(16)是開放型創新題；理科第(20)題有高等數學的背景，尤其是第(Ⅱ)設問奇特，突破常規、抽象性強、回避了復習資料，學生鮮見，在短時間內能否順利實現a與x的換位是解題的關鍵，這要求學生對函數概念有深刻的理解和把握，并能靈活應用，它終使“無數英雄競折腰”；這屬解法創新。理科卷將此題位置調前，考查學生的應變能力及個性品質。第21題是一個數列題，所給遞推關系式比較復雜，字母較多，快速將其變為
　　
　　
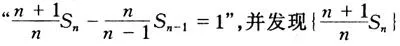
　　是等差數列不是件容易的事。而第(Ⅱ)問又融入了導數、增加了字母p，抽象程度越來越高，難度增大。第22題融雙曲線、平行四邊形、方程(組)、根與系數的關系、弦長公式等于一體，具有知識點多、覆蓋面廣、運算量大、綜合性強的特點。順利求解這三大題，沒有較強的理性思維能力是不行的。穩中求變，變中求新一直是高考命題追求的目標，今年也不例外。如選擇題第(9)題涉及“正八面體的外接球”，一變過去“正面四體的外接球”的老面孔，給人以新鮮感；選擇題第(11)題設問方式新穎，求解方法靈活；填空題第16題融閱讀、理解、識圖、發現、猜想于一體，具有背景新、內容新、方法新的特點；尤其是第20題的第(Ⅱ)問，以高等數學知識為背景設計問題，抽象函數關系式的結構簡潔，解法巧妙，數學思想方法蘊涵其中。這四題樸實大方，堪稱上乘之作，是整套試卷的創新亮點之所在，它們有效地考查了學生的創新能力。
　　2007年高考復習建議：時時關注新版《考試說明》，《考試說明》指出——選擇題、填空題和解答題題目的個數分別為10—12、4、6個，說明選擇題存在10個題的可能。
　　其次是關注高等數學初等化。一則高考命題者大多來自高校專家；再則高考是一種選拔性考試，它要考查學生進入高校繼續學習的潛能。因此高考題中幾乎每年都有幾道以高等數學為背景的題目。
　　6不等式受冷遇。去年高考數學全國卷(Ⅰ)多次考查不等式，其中理科壓軸第(2)問是一道不等式證明題，它難倒不少考生，但今年的考題明顯冷落了不等式。如此大的反差，出人意料，它提醒教師：不能引導學生猜題押題，明智的選擇是按考綱要求進行系統地復習。
　　7對向量考查力度不夠。向量是新增的重點內容，它融代數特征和幾何特征于一體，能與三角函數、函數、解析幾何、立體幾何自然交匯、親密接觸。向量作為代數與幾何的紐帶，理應發揮其坐標運算與動點軌跡、曲線方程等綜合方面的工具性功能。今年，不少省、市有這方面的高考試題，實屬情理之中；而我省的高考卷中，僅有第6題和第14題兩個基本題，第19題立體幾何也可以運用向量解法，但傳統方法更為簡單，無法凸現向量的價值，沒有出現向量與解析幾何的綜合題。向量處沒有新動作，有些出人意料，讓人遺憾。因此加大對向量的考查力度，充分體現向量的工具價值和思維價值，應該是今后高考命題的發展趨勢。
　　8該套題兩多一少。“兩多”是三角函數題多、解析幾何多；“一少”是數列題少。三角函數是新教材的軟肋，不僅是因為新教材刪除了舊教材中一半以上的三角公式，課時比例大大降低，而且很多知識點的要求層次也降低了，所以高三師生都不約而同到認為三角是最輕松的一章，是唯一可以稍事休息和小憩的場所。然而今年高考題卻在三角一章中直接出了三小一大合27分題，與公認的函數(27分)老大哥平起平坐了!解析幾何也有三小一大計27分，直接叫板函數的統治地位；而傳統重點內容、在學生心目中最規矩的數列只出了一個12分的大題。
　　看來，2007年的高考復習還得均衡發展，教材中的每一個章節內容都可能成為高考的熱點和重點，來的都是客，一個也不能少，哪個也不能輕視，不能人為地劃定三六九等，要一視同仁，穩扎穩打。最后還要關注創新題，盡量少用幾十年不變的陳題。如從報刊中涉獵新題，通過新題歸納解題的思維方法，激發頭腦的思維風暴；關注題型的單向發展，重視橫縱聯系；拓展新題的思想方法，加強多元交匯，使對知識的掌握達到“鷹擊長空，魚翔淺底”的境界。