三種幾何變換的主要作用

在現行的初中數學課本中^[1]，給出了平移、旋轉和軸對稱(即翻折)三種幾何變換. 它們都是不改變圖形的形狀和大小，只改變圖形位置的變換. 它們在中學數學教材的平面幾何理論體系中具有重要作用. 下面列舉幾個主要作用.

1 為判別相同的圖形提供依據和方法

在課本七年級上冊，關于畫出正方體的11種不同的表面展開圖，必須涉及到什么是相同的圖形；在七年級下冊，關于三角形全等的定義，又必須涉及什么樣的兩個三角形是相同的三角形；等等. 在沒有講任何圖形全等的相關定理前，需要選用過渡性“依據”去判別兩個相同的圖形，并且還要求這種過渡性理論“依據”必須易于學生理解和操作方法簡便. 筆者認為平移、旋轉和翻折變換是最合適的選擇對象.

把一個任意的平面圖形通過平移、或旋轉、或翻折變換，得到的新圖形一定是與原圖形全等的圖形. 雖然初中學生對它給出證明是困難的，但是用具體的平面圖形采用平移、旋轉和翻折變換后，它們不會改變原圖形的形狀和大小的事實可以說明它. 既然可用直觀方法說明上述客觀事實，那么就以“教學公理”形式來處理，把一個平面圖形通過平移、或旋轉、或翻折變換后，能與另一個平面圖形完全重合時，這樣的兩個平面圖形就可以叫做相同圖形或全等圖形. 因此，對畫出的兩種正方體的表面展開圖是否為相同圖形，就可以依據這三種幾何變換進行“圖形搬遷”的方法來判斷. 若搬遷后的兩個圖形能完全重合，則它們就是相同圖形；若用平移、旋轉和翻折的搬遷方法，總是不能使兩個圖形完全重合，則它們就不是相同圖形. 對三角形全等來說，課本給出了三角形全等的判定定理. 只要能確定兩個三角形有符合相關的三角形全等判定定理的條件，就可以獲得這兩個三角形全等的結論. 這可以避免用三種幾何變換進行圖形搬遷方法確定兩個圖形全等的冗長表述和圖形搬遷的麻煩. 解幾何題時，常要尋找兩個靜態的平面圖形間的相同關系，如果能通過動態過程確定兩個靜態的平面圖形是怎樣產生的，那么常常可以提供重要的解題信息和方法. 這說明三種幾何變換不僅是構造兩個圖形全等的重要工具，而且它們是不可忽視的證明兩個圖形全等的重要的解題思考方法. 利用運動變化觀念去認識事物符合辯證法.

2 為識圖和構圖提供指導思想和操作方法

在課本的七年級下冊編排了圖形的軸對稱變換內容，給出了軸對稱圖形和圖形成軸對稱. 在八年級上冊再安排了圖形的平移和旋轉變換內容. 課本以較大篇幅安排了幾何變換的應用實例，即把一個“簡單”的平面圖形，通過平移、旋轉、翻折變換，構造出許許多多復雜而美麗的“圖案”. 這樣既可以豐富學生對圖案的美感，又可以從圖案的構成方法去認識圖案的結構. 特別是對“基本圖形”的不同選擇，運用不同的變換方法可獲得某些相同的特殊圖形. 由于“基本圖形”的相對性，事物運動變化的多樣性，這有利于培養學生的辯證唯物主義的認識觀. 課本通過上述指導思想和具體操作方法，結合課本的配套練習，能有效地培養學生的識圖和構圖的能力.

3 為證明平面幾何習題提供重要的動態分析方法

解題的本質是把題目的條件信息和結論信息建立起科學的聯系^[2]. 解題的表述就是闡述其科學聯系的建立過程的具體理由. 在這種意義上說，解(證)幾何題就需要不斷地變換前后步驟的“形式”或“思想”. 解數學題的靈魂就是“合理變化”. 合理的變化中常會拓展出解題所需要的一片新天地，缺失合理變化時常會在呆滯中一籌莫展. 既然解證幾何題需要不斷地合理變化，那么解(證)幾何題的分析就必須適時運用運動變化的觀點和方法.

因為絕大多數“靜態”的數學題都是在某種動態環境下，靜止于某種特殊情況時的特殊狀態，它就像“運動物體”在某一時刻的所拍下的“照片”，所以要把數學題賦予為“靈性之物”，要研究它由誰以怎樣的運動方式產生，靜止于何時之狀. 對于全等圖形來說，就需要觀察分析圖形的平移、旋轉和翻折運動，明確數學題中的圖形是通過怎樣的運動形成. 讓相關的圖形“動起來”之后，就能突顯它們之間特殊的位置關系和大小關系，就容易從中分析捕捉到重要的解題信息和發現解題方法. 例如：

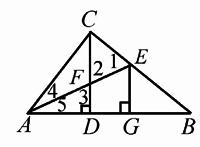
圖1

題1 已知：如圖1，△ABC，∠ACB=90°，CD⊥AB于D，AE是△ABC的角平分線，AE交BC于E，AE交CD于F， EG⊥AB于G，

求證：CF = EG.

(1)用動態分析方法研究題1構成機理，發現題1的解題信息

①從相關圖形旋轉考慮

如圖1，給定Rt△ABC，斜邊AB上的高CD就確定了. 把射線AE繞點A沿逆時針方向從AB旋轉到AC時，點E由點B運動到點C，同時點F由點D運動到點C，點G由點B運動到點D，于是CE由BC退縮為點C，CF由CD退縮為點C， 線段EG在平移中由點B逐步“長高”到CD. 因為在此運動中，CE 、CF與EG都是同時開始、同時結束的連續變化的線段，且CE與CF都由長變為短，EG由短變長，它們的長度“最小值”都是零，所以必有CE = EG和CF = EG.

當CE = EG時，又AE是公共斜邊，所以Rt△AEC≌Rt△AEG(HL定理)，所以∠4=∠5. 此時，AE正好是△ABC的角平分線.

反過來，只要在動態的變化中把“AE是△ABC的角平分線”的特殊情況“靜止”下來，那么題1的條件就全有了，并且依據角平分線性質定理，立即可得∠4=∠5，CE = EG(角平分線上的點到角的兩邊距離相等). 在Rt△AEC和Rt△AFD中，因為∠1與∠4互余，∠3與∠5互余，又∠4=∠5，所以∠1=∠3. 因為∠2與∠3是對頂角，所以∠2=∠3. 所以∠1=∠2，所以CE =CF. 又CE = EG，所以CF = EG.

這種利用某圖形旋轉建構動態分析，既能說明題1的存在性和這種構造理由，又能探究出題1的一種證明方法，且發現了與結論相關的線段CE是證明本題之關鍵.

②從相關圖形的軸對稱考慮

對題1，給定Rt△ABC，斜邊AB上的高CD就確定了. 因為AE是Rt△ABC的角平分線，所以∠4=∠5. 又Rt△ABC的直角邊AC必小于它的斜邊AB，所以把Rt△AEC沿AE翻折180°，所以AC必然落在AB上，從而得到Rt△ABC關于直線AE對稱的△AEG. 因為∠ACB=90°，所以EG必垂直AB于G. 這就有了題1的全部條件. 也找到了從“證明三角形全等”入手的解題方法. 易證∠4=∠5，∠ACB=∠AGE=Rt∠，又AE是公共邊， 所以Rt△AEC≌Rt△AEG(AAS)，所以CE = EG，∠1=∠AEG. 又因為EG⊥AB，CD⊥AB，所以CD∥EG，所以∠2=∠AEG. 又∠1=∠AEG，所以∠1=∠2，所以CE =CF. 又CE = EG，所以CF = EG.

這種利用某圖形翻折建構動態分析，既能從新的角度說明題1的存在性和構造理由，又能探究出題1的新的證明方法. 此外，還可以從中收獲其他解題信息，例如：由于兩個圖形關于直線對稱，對稱點的連線被對稱軸垂直平分. 所以AE垂直平分CG，所以CF =FG，CE = EG(線段垂直平分線上的點，到線段兩個端點等遠). 等等.

③從相關圖形的平移考慮

如圖1，給定Rt△ABC，斜邊AB上的高CD就確定了. 讓直線EG從CD開始向右平移到經過點B，讓直線FG從BC開始向下平移到經過點D，對應的線段EG和FG都分別由長變短，它們的長度“最小值”都是零，所以必有FG = EG情況存在. 而夾在兩平行線之間的平行線段相等，所以有CF = EG. 在此特殊情況下，必有CE = EG，由于有∠ACB=Rt∠，EG⊥AB于G的給定條件，所以AE也正好是△ABC的角平分線. 由于相關的部分圖形的對稱性，此時點F就在AE上. 這就說明了題1成立，找到了證明CE = EG是證明題1的關鍵.

(2)用動態分析方法研究題1的關聯題，探究變式解題教學方法.

在題1的條件下，由上述分析和推理已知CF = CE = EG，又CF與 EG都垂直于AB，所以四邊形CFGE是菱形. 于是把題1改造成題2

題2 已知：如圖2，△ABC中，∠ACB=90°，CD⊥AB于D，AE是△ABC的角平分線，AE交CD于F，AE交BC于E，EG⊥AB于G，

求證：四邊形CFGE是菱形.

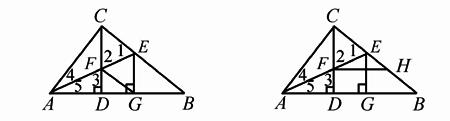
圖2

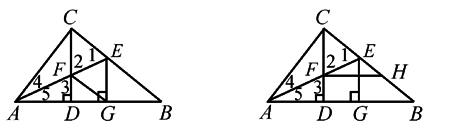
圖3

在題1的條件下，由上述分析和推理已知CF = EG，又CF與 EG都垂直于AB，若再作FH∥AB交BC于H，于是可推出Rt△CFH≌Rt△EGB(AAS)，從而有CH=EB. 所以有CH-EH=EB-EH，即CE=BH. 于是把題1改造成題3

題3 已知：如圖3，△ABC中，∠ACB=90°，CD⊥AB于D，AE是△ABC的角平分線，AE交CD于F，AE交BC于E，EG⊥AB于G，FH∥AB交BC于H，

求證：CE=BH. (或求證CF=BH)

綜上所述，在解題教學中探究關聯題的變式聯系，也常需要對數學題及它們的解答進行動態分析探究.

物質的世界里，事物的運動變化造就了事物間的聯系形式具有多樣性. 許多事物的“隱蔽”聯系形式常需用動態分析方法去探究發現. 從哲學意義上說，“解題”就是不斷探究發現“未知世界規律”的過程，因此解題教學要重視關聯題的研究，加強變式解題示范，充分發揮三種變換的作用，適時運用動態分析的研究方法去解題.

參考文獻

[1] 馬復主編.義務教育課程標準實驗教科書《數學》 (七年級下冊 八年級上冊 )[M].北京師范大學出版社，2005.

[2] 邱衛平.建構“選擇·探究·發展”的解題教學模式@提高中學數學的解題教學效率[J].數學教育研究，2006，(1).

作者簡介 邱衛平 (1953-)，男，湖南常德人，中學數學高級教師，特級教師，長期從事中學數學教學與研究，曾參與深圳市中考數學考試說明的編寫與修改，多次擔任深圳市中考數學命題組長，先后多次擔任過中考閱卷組長和閱卷質量檢查組長.