艦船管路流體脈動衰減器的性能研究

1 引 言

艦船管路系統中,如液壓系統、燃油系統、冷卻水系統,由于工作過程的不完善,伴有工作介質的振蕩或脈動。介質脈動所產生的交變力,使管路及其連接的附件形成振動。強烈振動會使管路附件(包括彈性接管) 以及它們之間的連接部分松動或破裂,并引起船體的結構振動，而且也導致艦船振動噪聲較大，這將嚴重影響艦艇的隱身性能。所以，如何有效地降低管路系統的振動和噪聲是目前艦船振動和噪聲控制中一個非常重要的問題。

目前，降低管路脈動除了改進管路設計，安裝低噪聲閥等措施外，另一個主要的手段就是安裝流體脈動衰減器，如: 蓄能器、λ/4 管道消音器(擴張管式) 、λ/4 旁支共鳴器、赫姆霍茲共鳴器以及多腔共鳴器等[1]。國內外在蓄能器和脈動衰減器及其系統諸多性能的研究方面，己經做了大量的研究工作，并取得了很好的成果[2,3]。

本文研究了一種改進的赫姆霍茲共鳴器類型的流體脈動衰減器的性能，其作用機理類似于有阻尼的動力吸振器，結構形式類似于蓄能器。采用流體網絡理論方法建立衰減器的集中參數等效線路模型，在此基礎上求得系統各點阻抗及脈動衰減器的插入損失，并分析了衰減器衰減效果的影響因素。

2 流體網絡理論基礎

流體網絡理論是由研究管內流體傳輸與瞬變而發展起來的一門應用科學。它可以用來分析發生在工業動力裝置、控制測量裝置和生物醫學工程等，各種流體管路系統中功率和信息的傳輸過程，以及由于擾動引起的各種流體瞬變現象。流體網絡理論主要涉及兩個學科的內容，一是流體力學，二是電氣網絡和傳輸線理論。流體力學雖然是一門古老的學科，但它在與其他有關學科結合的發展過程中，逐漸形成許多新的學科分支，如高速空氣動力學、電磁流體力學、流控流體力學等。流體力學在和電氣網絡理論相結合的過程中，也正在逐漸形成流體網絡理論這樣一個新的學科分支。

由于流體(氣體和液體)是自然界中最基本和最常見的一種介質，各種利用流體作為動力或用流體作為控制和測量手段的流體裝置，在各個生產領域中是最常見的。在這些流體系統中，各個元件之間的功率和信息都是通過管路來傳遞的。因而，管內流體傳輸與瞬變的問題在許多生產領域中經常發生，如流控技術和氣動、液壓技術中的動態過程分析；水電站設計和運行中的水擊現象研究；天然氣、石油和工業壓縮機管路中的壓力波動和壓力諧振，以及它們的消除措施；柴油機進排氣管系的脈動分析和利用；流體濾波器和消聲器的設計計算；儀器儀表中流體動態測試的精度確定以及生物流體力學中的血液流動的研究等。研究這些與各種實際問題有關的管內流體傳輸與瞬變問題，對正確設計和合理使用一個流體動力及流體控制系統顯然是十分重要的。對于流體管路系統的傳輸和瞬變問題，如果能將它們作為一個流體網絡問題來處理，就有可能利用比較成熟的網絡理論對它們進行分析計算，可以比較容易地得出在工程上有實用價值的結果。因而這門學科的建立和發展，將會大大促進管內流體傳輸和瞬變問題的研究工作，無論在理論上或是實際應用上都是十分重要的。

2.1 流體網絡的特點和研究方法

流體網絡理論是由研究管內流體傳輸與瞬變而發展起來的一門應用科學，流體的傳輸和狀態的變化都發生在特定形狀和尺寸的元件與管路中，形成管路內部的復雜流動。它具有如下一些特點：

1) 流體管路的軸向長度大于其橫向長度，其軸向流動速度遠大于其橫向流動速度。因而可以略去橫向流動速度分量，認為所有流動參數(速度、壓力等)是沿管路橫截面求平均值。

2) 流體的流動參數(壓力、速度或流量)不僅隨位置變化而變化，而且還與時間有關。即流動是隨時間和位置而變化的，這時的流動參數是軸向距離x與時間f的函數，稱為一元不定常流動。

3) 流源壓力(或擾動壓力)的波形可以是正弦波、矩形波，也可以是按一定函數規律變化的規則與不規則波形。

4) 流體傳輸與瞬變不僅在簡單的單管路中進行，在許多情況下往往是在以網絡形式出現的管系中進行的。這個管系既包含有許多分布參數的主管路和分叉管路，又包含有許多集中參數的流體元件。

管內流動還受到許多因素如流體慣性、粘性、壓縮性、熱傳導、管路的幾何形狀及管路端部阻抗等的影響，而變得十分復雜。但是，通常關心的只是管系中各個管路連接點處的壓力和流量的瞬態特性，以及它們如何受到流源、管長、管徑以及終端、始端阻抗等的影響，而對于管路內部流動機理的詳細過程一般并不要求了解。這就使我們有可能把一個流體管系考慮為一個流體網絡，把流體管系的傳輸和瞬變問題轉化成一個只是求流體網絡各個節點的瞬態壓力和流量的問題，從而避開了單純從流體力學方法去解決時所遇到的一些困難。由于在電氣網絡中已經有了比較成熟的理論和一套系統的分析計算方法，因而很自然地會聯想到能否在一定的假設條件下，用電氣網絡的方法去解決流體網絡的問題。只要在流體網絡和電氣網絡各個參數之間建立一定的模擬關系，在線性化的假設條件下，從流體力學基礎方程出發所導出的流體傳輸方程和等效線路與電氣網絡中相應傳輸方程和等效電路，其形式是完全相同的。這說明可以利用電氣網絡中的許多概念和方法去解決流體網絡中的傳輸和瞬變問題。

2.2 流體網絡的基本參數

在電學中，電的性質集中表現為電熱效應、電荷積聚和電磁感應3種現象，它們用電阻、電容和電感3個基本參數[4]來表示。在流體流動中也表現出類似的現象，通常用流阻、流容和流感來比擬對應的電學參數。此外，我們還把壓力差△p比擬為電壓，把流量Q比擬為電流。流量通常有三種表示方法，其一為體積流量QV，它為單位時間流過某截面的流體的體積量；其二為質量流量QM，它為單位時間流過某截面的流體的質量；其三為重量流量QW，它為單位時間流過某截面的流體的重量。

由于本文研究的脈動衰減器腔室內氣體質量保持不變，變化的參數為其體積和密度，故在計算流體網絡參數時使用體積流量QV，由定義知

QV=AP·ν

(1)

1) 流阻

在流體網絡中，由于流體的粘滯力表現出對流體運動的抵抗，它導致與壓力相聯系的能量損失。與電阻的定義類似，把定常流動狀態下的流體部件的流阻定義為該流體部件兩端的壓力差與通過它的流量之比，即：R=Δp/Q，則體積流阻為

RV=Δp/QV

(2)

2) 流容

實際流體都存在可壓縮性，對于液體來說，要在較大的壓力下才能表現出來。任何體積一定的容器都具有與可壓縮流體相聯系的流體容量。容器內壓力的變化會引起其中流體質量的變化，容器內流體質量隨壓力的升高而增加，即容器內將產生質量的聚集。流體的體積流容定義為體積的變化與引起體積變化的壓力變化之比，即：

(3)

3) 流感

在流體網絡理論中,任何發生高速瞬態流動的地方，都會由于流體的慣性使流體質量加速或減速，導致壓力的變化。與電學中的電感定義相對應，體積流感可以定義為管兩端的壓力變化與流量變化率之比，即：

(4)

簡化可得

(5)

3 脈動衰減器數學模型的建立及其性能研究

3.1 脈動衰減器數學模型的建立

3.1.1脈動衰減器的工作原理

本文研究對象為一種改進的赫姆霍茲共鳴器類型的流體脈動衰減器，其作用機理類似于有阻尼的動力吸振器，結構形式類似于蓄能器。它與活塞式蓄能器的根本區別在于：活塞式蓄能器通過封閉容積內氣體的壓縮膨脹來補償管道內的流量脈動而起作用[5]；而這里提出的裝置則通過活塞2的質量來吸收管道脈動能量而起作用。它通過高密度的金屬質量代替傳統赫姆霍茲共鳴器頸口處的等效液體質量，以低體積彈性系數的氣體代替腔中的可壓縮性很低的液體，從而可以在相同的體積下，使共鳴器的固有頻率設計得更低，也就是說該裝置相對傳統的赫姆霍茲共鳴器，其結構可以做得更加緊湊。

根據動力吸振器的原理[6]，當附加彈簧系統的固有頻率與激勵力頻率相同時，會出現反共振現象,從而消除主系統的振動。在實際液壓管道系統中,應用此原理是有依據的,這里對該衰減器作簡單介紹(圖1)。裝置安裝在液壓管道1上，質量為m的工作活塞2與空氣彈簧3構成一簡單的振動子系統。阻尼主要歸因于氣體以及工作活塞與缸壁之間密封處的剪切應力。因為缸內間隙處的液體容積相對空氣彈簧3的容積要小得多，另外液體的體積彈性系數也要比氣體的大得多，所以可以認為工作活塞所受的彈性恢復力主要由空氣彈簧提供。

3.1.2脈動衰減器的數學模型

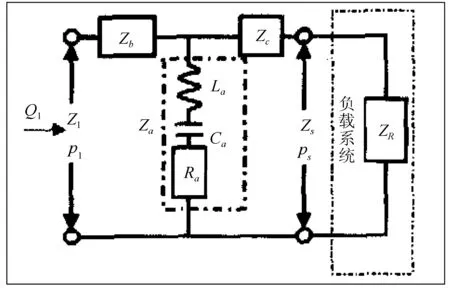
圖2 脈動衰減器等效電路

圖中Zb是工作活塞前連接泵及衰減器的一段短管的阻抗；Zc是工作活塞后連接泵及負載的一段短管的阻抗；Za是衰減器的阻抗；衰減器的阻抗Za由工作活塞引起的流感La、空氣彈簧引起的流容Ca、衰減器的阻尼引起的流阻Ra組成。

m表示活塞質量，腔內氣體質量可忽略不計，故m亦表示衰減器的質量；Ap表示活塞的橫截面積；負載系統阻抗設為Zs。

1)La

活塞受到流體的沖擊力為ΔF=Δp·AP

且

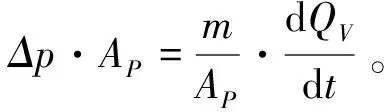
則

(6)

2)Ca

空氣彈簧的剛度

(7)

所以

(8)

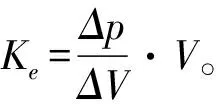
3)Ra

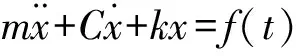
(9)

(10)

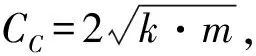
(11)

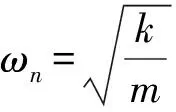
3.2 脈動衰減器的性能研究

3.2.1液體管路的阻抗

通常認為液體是不可壓縮流體，其流容非常小，可忽略不計，故只考慮管路液體的流阻效應和流感效應。

氣壓力降和速度的關系可表示為：

式中，μ表示流體粘性系數。

因而得體積流量QV與壓力差△p之間的關系為

故層流型圓管線性流阻的表達式為：

由此得液體管路的阻抗：

(12)

(13)

式中，d表示排水管道的通徑；lb表示輸入管道的長度；lc表示輸出管道的長度。

3.2.2脈動衰減器的性能研究

在線性電路理論中，圖1為一帶有負載的無源T形四端網絡，其傳遞矩陣[A]為：

=

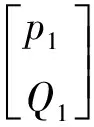
Qs=Ps·Zs，得

因此，輸出端的壓力脈動為:

(14)

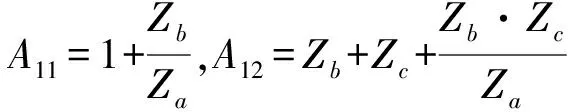
(15)

若未安裝脈動衰減器(Za=∞)，輸出端的壓力脈動為:

(16)

(17)

聯合式(11)、(12)、(13)和式(17)即可求得脈動衰減器的插入損失，初步評估其衰減性能。

4 結 論

式(15)反映了衰減器輸出端脈動壓力的變化規律，可以看出衰減器的作用就相當于在主系統中附加了一有阻尼的動力吸振器。根據動力吸振器的原理，恰當調諧衰減器的固有頻率ωn使之與管道中流體脈動的頻率ω相近，就可以大幅降低后接管道中的流體脈動。

本文在通徑為60 mm的排水管道上加裝脈動衰減器，前后管道均長600 mm。通過篩選，確定衰減器的主要參數如下：工作活塞質量為25 kg，直徑為300 mm，空氣彈簧的容積為30 L，預壓力為3 MPa。圖3就是相應參數條件下衰減器模型的插入損失曲線。

由圖3可見，在衰減器的固有頻率26 Hz附近，該衰減器模型具有約43 dB的插入損失；在高頻部分，插入損失會穩定于30 dB附近。

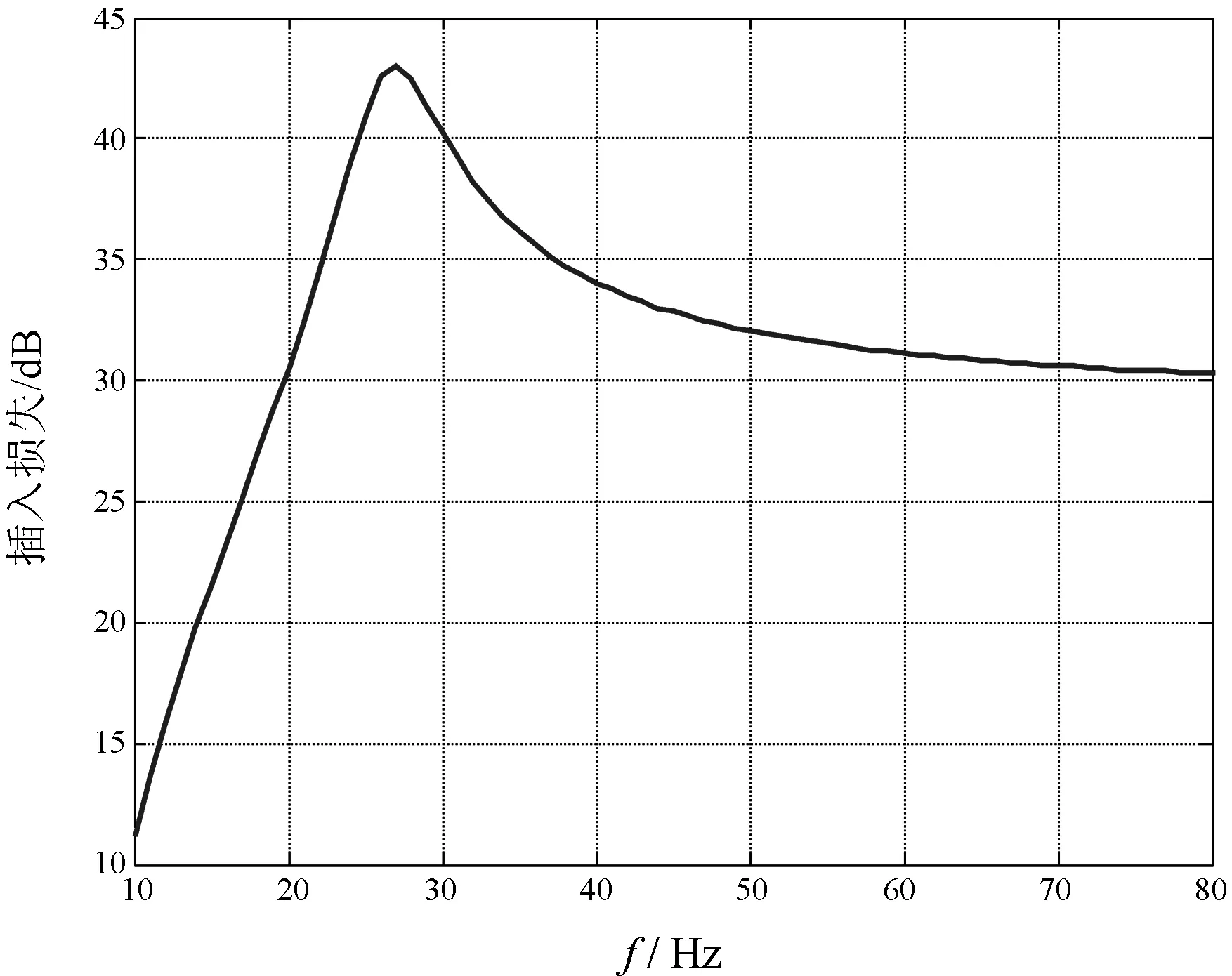
圖3 插入損失曲線

另外，可以適當增加阻尼系數ξ，使整體衰減效果比較穩定；還可以借鑒多腔共鳴器的原理，設計成多級衰減器。通過改變空氣彈簧的預充壓力可以非常方便地調節衰減器的固有頻率，使之與管道內流體脈動的工況相適應，從而實現良好的流體脈動衰減效果。

[1] 王伯良．噪聲控制理論[M]．武漢：華中理工大學出版社，1990．

[2] ROBERT E, MEYERS. Accumulator with temperature Compensation [P]. US，US3893486, 1975.

[3] TRIKHA A K. An efficient method for simulating frequency dependent friction transient liquid flow [J]. Journal of Fluids Engineering, 1975,97(1)：97-105.

[4] 羅至昌．流體網絡理論[M]．北京：機械工業出版社，1988．

[5] 謝坡岸，王強．蓄能器對管路流體脈動消減作用的研究[J]．噪聲與振動控制，2000(4)：2-5．

[6] 谷口修(日)．振動工程大全(上冊)[M]．北京：機械工業出版社，1983．

[7] 蘇爾皇．管道動態分析及液流數值計算方法[M]．哈爾濱：哈爾濱工業大學出版社，1985．