解決問題策略的教學實踐與思考
章 莉
《數學課程標準》對“解決問題的策略”提出了明確要求:形成解決問題的一些基本策略,體驗解決問題策略的多樣性,發展實踐能力和創新精神。教師在教學中應科學合理地制定教學目標,激發學生學習策略的動機,關注策略的形成過程、策略的價值、策略背后的思想,而不是把策略當成結論性知識或程序性技能傳授給學生。
一、讓學生產生學習策略的需求
教學時注意創設情境,喚醒已有的知識、經驗,制造認知沖突,能激發學生主動尋求解決問題策略的熱情。
情境1育華實驗小學要舉行乒乓球比賽,有15名選手參加。如果每2名選手間進行一場比賽,一共要賽多少場?
學生開始都會根據以前的學習經驗,嘗試運用畫圖的策略來解決情境中的問題。但是在探究過程中學生感到運用畫圖策略來解決比較麻煩。
教師創設參賽選手人數較多的情境,讓學生感受解決問題的復雜性,一方面可以引發學生積極思考,產生從簡單人手策略的強烈心理需求;另一方面可以促使學生初步認識從簡單人手策略的內涵,即它是一種迂回策略,而不是從簡單到復雜的循序漸進。
二、讓學生經歷策略的形成過程
解決問題的策略不同于解決問題的方法。方法可以在傳遞過程中習得,但策略只能在方法的實施中感悟獲得。教師要準確定位策略教學的目標,讓學生體驗策略的形成過程,并從中獲得對策略內涵的認識與理解。
(一)潛意識階段
上述情境中的問題,教師可引導學生進行下列學習活動:
1引導:這個問題比較復雜,可先從最簡單的情況人手,看看其中有沒有規律。
2思考:①從多少人比賽開始研究?②當比賽人數一定時,怎樣有順序、有規律地呈現選手間的比賽情況?③比賽場數與參賽人數之間有怎樣的聯系?
3學生分組活動。
4全班交流,展示典型方案。

5討論:隨著比賽人數的增加,比賽場數是怎樣變化的,其中有什么規律?
6,應用規律:15名同學參加比賽,一共要比賽多少場?怎樣列式?
7回顧:解決15人的比賽場數問題時是怎樣思考的?(從簡單情形人手)
8反思:為什么要運用從簡單人手策略?運用從簡單入手策略解決問題時一般是怎樣做的?
學生在豐富多樣的數學活動中經歷了“遇到復雜問題一解決同類簡單問題一探究解決簡單問題時的規律一應用規律解決較復雜問題”的過程,初步體驗到從簡單人手策略的形成過程。
(二)明朗化階段
情境2有一個生日蛋糕,只準垂直向下切,不準水平橫切,10刀最多能將一塊圓形蛋糕切成多少塊?
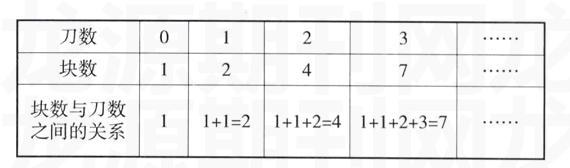
新問題呈現后,組織學生思考可以用什么策略解決,使學生具有明確的應用策略的意識。學生都會自覺運用從簡單人手策略,通過畫圖尋求答案。為了便于發現其中的規律,教師引導學生從切O刀的情況畫起,并列表整理答案。(表格見P49)
引導觀察:從第2列開始,每一列與前一列比較,切幾刀,最多能切出的塊數就是在前一列塊數的基礎上多幾。學生根據塊數與刀數之間的變化規律順利解決新問題。
問題解決后,再組織學生交流解決問題的過程。這樣,隨著解決問題策略的初步應用,學生對從簡單人手策略的認識開始明朗化。
(三)深刻化階段
解決比賽場數及切蛋糕塊數問題都是從簡單人手,借助畫圖或列表策略,從中發現規律,進而解決問題的。為了防止學生思維定勢,認為運用從簡單人手策略解決問題就要借助畫圖或列表策略,教師可再設計其他的拓展練習。情境31/(1998+1999)+1/(1999+2000)+1/(2000+2001)+……+1/(2008+2009)
解決這個問題也可從簡單人手,先研究1/(1×2)+1/(2×3)+1/(3×4)+1/(4×5)中的計算技巧,再推廣到原問題去解決。在這一解題過程中,盡管也是運用從簡單人手策略,但沒有依靠畫圖或列表策略。而是滲透了猜想—舉例—驗證的策略。之后,教師要引導學生反思運用從簡單人手策略的解題過程,使學生對策略的本質有更深入的認識,促進學生形成穩定的解決問題的策略。同時,學生在不斷整合、應用不同策略解決問 題的過程中,體驗解決問題策略的多樣性,培養了學生面臨新問題靈活運用各種策略解決問題的意識。
三、讓學生體驗策略的應用價值
解決問題策略的價值不僅僅是解決某一類問題,獲得某一類問題的結論,更重要的是在解決問題的過程中基于解題的經歷,形成相應的經驗、技巧、方法,進而通過反思和提煉,對策略本身有更深刻的理解,形成解決問題的基本策略,并體會策略的價值。
教師可這樣引導學生回顧反思:為什么要使用從簡單人手策略?使用該策略有什么好處?在什么情況下使用該策略?學生在自我內化的過程中感受策略給解決問題帶來的便利,體會策略的價值,增強運用策略解決問題的自覺性。
四、讓學生感悟策略背后的數學思想
數學學習的核心在于數學思想方法的建立。教師要通過策略的教學,幫助學生不斷積累數學活動經驗,感悟策略背后的數學思想。
學習問題1、2、3之后,教師應引導學生將實際問題抽象成數學模型。可設計這樣的提問:①當參賽隊員為n名時,一共要比賽多少場?②當切n刀時,最多可切多少塊?③當從1/(1×2)+1/(2×3)+1/(3×4)+……一直加到1/(n×(n×1))時,怎樣計算?學生通過抽象化、符號化,構建相應的數學模型為:①比賽場次是(n×(n-1))/2;②最多切的塊數是(n×(n+1))/2+1;③計算方法是: 1-1/(n+1)=n/(n+1)。
學生從簡單人手發現規律,構建數學模型的過程也是一個歸納推理的過程。教師要使學生通過策略的運用,模型的建立,感悟從簡單人手策略背后的數學思想——歸納推理思想,從而提升學生的數學思維能力,培養學生的數學素養。
(責編林劍)

