淺談不定積分和定積分的課堂教學

羅 萍 張翠花

【摘要】本文采用對立統一的教學方法,強調了高等數學中不定積分與定積分既對立又統一的兩個方面,以期提高積分學的課堂教學效率,為學習積分學的學生提供幫助與借鑒。

【關鍵詞】積分學不定積分定積分

積分學中有兩個重要的基本概念:不定積分和定積分。能否正確地理解這兩個概念是能否學好積分學的關鍵。由于這兩個概念名稱相近,容易讓人混淆,所以在課堂教學過程中,我們嘗試采用對立統一法,使學生較好地掌握這兩個概念,取得了良好的教學效果。

首先,在教學過程中,我們特別強調不定積分和定積分這二者對立的一面。他們的不同之處在于:

第一,定義不同。(1)不定積分的定義:如果F(x)是f(x)在區間I上的一個原函數,則稱f(x)的所有原函數F(x)+C為f(x)在I上的不定積分。記作∫f(x)d(x)=F(x)+c。(2).定積分的定義:設f(x)是定義在區間[a,b]上的有界函數,用分點a=x₀∠_x1∠...∠_n=∠將區間[a,b]分成n個小區間[x_i-1,x_i](i=1,2,…,n),其長度為△x_i=x_i-x_i-1,在每個區間[x_i-1,x_i]上任取一點ξ(x_i-1≤ξ_i≤x_i),則乘積f(ξ_i)△x_i(i=1,2,...,n)稱為積分元素,總和S_n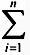f(ξ_i)△x_i稱為積分和。當n無限增大,而△x_i中最大者△x→0(△x=max{△x_i})時,總和S_n的極限存在,且此極限與[a,b]的分法以及點ξ_i的取法無關,則稱函數f(x)在區間[a,b]上是可積的,并將此即限值稱為函數在區間[a,b]上的定積分,記為:

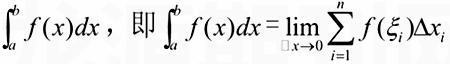
由定義可知,不定積分的實質是被積函數的全體原函數的總稱,即不定積分是函數;而定積分是和式極限,實質上是數值。這是兩者在定義上的區別。

第二,記號不同。不定積分通常用∫f(x)d(x)表示;而定積分記為∫^b_af(x)dx。顯然,不定積分無積分上下限,而定積分必須有積分上下限。

第三,求不定積分與求定積分的任務不同。

求函數f(x)的不定積分,其任務是求f(x)的所有原函數。通常是運用不定積分的基本公式及換元法、分部積分法等求出f(x)的一個原函數F(x),則不定積分∫f(x)d(x)=F(x)+C。定積分的任務卻側重于運用不定積分的知識(這是兩者統一之處,后面有詳述)求出一個值來。

第四,幾何意義不同。

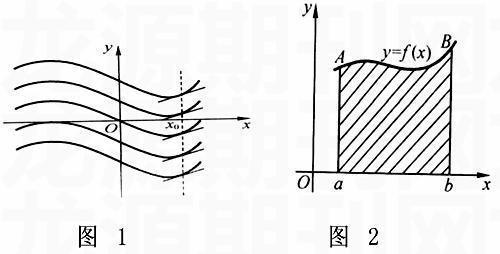
不定積分∫f(x)d(x)=F(x)+C中含有任意常數C,因此,對于每一個給定的C,都有一個確定的原函數。在幾何上相應地就有一條確定的曲線,稱為f(x)的積分曲線。因為C可以取任意值,因此,不定積分表示f(x)的一簇積分曲線。而函數f(x)正是積分曲線在x點處的斜率。由于積分曲線簇的每一條曲線,對應于同一橫坐標x=x0的點處有相同的斜率,所以對應于這些點處,它們的切線互相平行,任意兩條曲線的縱坐標之間相差一個常數,所以積分曲線簇y=F(x)+C中每一條曲線都可以由曲線y=F(x)沿y軸方向上、下移動而得到,如圖1所示。

而定積分∫^b_af(x)dx的幾何意義是:當在區間[a,b]上的連續函數f(x)≥0時,∫^b_af(x)dx表示y=f(x), x=a,x=b及x軸所圍成的區邊梯形的面積;而f(x)≤0時,這時的∫^b_af(x)dx表示y=f(x),x=a,x=b及x軸所圍成的區邊梯形面積的負值;如果f(x)在[a,b]上既有正值又有負值,此時,∫^b_af(x)dx表示y=f(x),x=a,x=b及x軸所圍成的圖形中,位于x軸上方的面積之和減去位于x軸下方圖形的面積之和,如圖2所示。お

由上可知,不定積分和定積分確實是兩個完全不同的概念。

然而,世界上的一切事物都包含著既相互對立又相互統一的兩個方面,不定積分和定積分雖然有以上諸多不同之處,但二者名稱僅差一個“不”字,是否它們之間存在必然的內在聯系呢?答案是肯定的。

不定積分和定積分確實有統一的一面,聯系它們的橋梁是牛頓萊布尼茲公式。牛頓萊布尼茲公式告訴我們:若函數f(x)在區間[a,b]上連續,且F(x)是f(x)的一個原函數,則∫^b_af(x)dx=F(b)-F(a)。由此公式可知,要求定積分∫^b_af(x)dx的值,只要求出f(x)在[a,b]上的一個原函數F(x),并計算出F(x)從端點a到端點b的改變量F(b)-F(a)即可。

因此,定積分與原函數有了聯系。而求原函數正是不定積分的任務,所以要計算出定積分的值,先得求出不定積分,從這個意義上來說,不定積分是定積分的基礎,定積分是不定積分的應用,這就是它們統一的一面。