“圓與圓的位置關系”教學設計

崔亞娟

本節課是人教版義務教育課程標準實驗教科書《數學》九年級上冊第二十四章《圓》中“圓與圓的位置關系”.本節課是學生在已掌握了點與圓的位置關系、直線和圓的位置關系等知識的基礎上,進一步研究平面上兩圓的不同位置關系.本節課采取類比的方法進行教學,通過本節課的學習可以培養學生動眼、動手、動口等能力,同時也滲透了類比、數形結合的數學思想.圓與圓的組合圖形具有一些特殊的位置關系和性質,因此在實際生活中有著廣泛的應用,尤其在工業制造方面應用較多.

【教學目標】

1.結合圖形辨認圓與圓5種位置關系,根據具體圖形說出相應的位置關系名稱,能類比直線與圓的位置關系,通過公共點個數來決定圓與圓的5種位置關系.了解兩圓外切,內切與兩圓圓心距d半徑R和r的數量關系的聯系.

2.經歷探索兩個圓之間位置關系的過程,訓練學生的探索能力.通過平移實驗直觀的探索兩個圓之間位置關系,發展學生的識圖能力和動手能力操作.

3.通過探索圓與圓的位置關系,體驗數學活動充滿著探索與創造,感受數學的嚴謹性以及數學結論的確定性.經歷探究圖形的位置關系,豐富對現實空間及圖形的認識,發展形象思維.

【教學重點】

通過探索圓與圓的位置關系了解兩圓外切,內切與兩圓圓心距d,半徑R和r的數量關系的聯系.

【教學難點】

探索兩個圓之間的位置關系 ,以及外切,內切與兩圓圓心距d,半徑R和r的數量關系的過程.

【教學方法】

實驗探索,指導學生觀察、實驗、探究、歸納.

【教具準備】

多媒體課件、學生用表格、圓規,鉛筆,尺子,兩個半徑不一樣的圓形紙片.

【教學設計】

一、激情導入,動情入境

師:首先讓我們一起來觀看一組動畫,注意觀察,看你都發現了什么.

1.大屏幕展示FLASH動畫,演示水滴下落的情境.

(通過動畫演示水滴落入水中的情境,展示給學生一個生動、形象的圓與圓位置關系的實際場景.導入新課寓趣味于其中,既體現了數學源于生活,又能激發學生的興趣,喚起他們的好奇心與求知欲.本環節的設計是通過生活中比較常見的水滴下落到水中形成的水波來創設情境,能夠讓學生在開課伊始就入情入境.)

2.提出問題.

師:回憶剛才的動畫演示,猜想一下,我們這節課要研究的主題是什么?

學生試著說出本節課所要研究的主題——圓與圓的位置關系.

師:生活中存在著很多圓與圓的位置關系的實例,你能根據你的生活經驗找找看嗎?

學生思考、回憶、尋找,并試著談出自己找到的有關圓與圓位置關系的實物.

(通過尋找生活中的圓與圓位置關系的實物,再次加深對本節課所要研究內容的印象.)

師:今天老師也給大家帶來了一些圖片,讓我們來一起欣賞一下吧!

大屏幕展示教師帶給學生的圖片.總結圖片中圓與圓位置關系在生活中的重要性.

(通過展示圖片,可以發現圓與圓的位置關系在我們的生活中起到一定的裝點作用,同時也有它的實用價值.本環節旨在讓數學貼近生活,既強化學習目標又激發學生的學習興趣,使學生的學習活動有鮮明的目的性.通過學生自己去找尋生活中圓與圓的位置關系來增強其對本節課學習內容的認識.并且學生能感悟數學來源于生活的客觀真理.)

二、實驗探究

1.動手操作.

師:請同學們拿出課前準備好的兩個半徑不相等的圓,放在桌面上,固定其中一個圓不動,在桌面上移動另一個圓,觀察兩圓的位置關系和公共點的個數.

大屏幕展示自學探究內容:

(1)觀察兩圓的位置關系和公共點的個數.

(2)根據你的操作,類比直線與圓的位置關系,你能給他們分別命名嗎?

(3)在幾種圓的位置關系中,你都能得到哪些結論,看哪一個組找得多.

2.自學探究.

學生實驗,教師巡視學生的探究過程,并給予相應的指導和幫助.

3.小組匯報.

師:哪個小組愿意勇敢地到前面來匯報一下自己組的探究結果?

類比前兩節研究點與圓的位置關系,直線與圓的位置關系,學生能夠很容易對圓與圓的位置關系探究思路理解,并進行操作.通過學生的親自動手操作加強學生對兩圓5種位置關系的認可.初步感知兩圓的5種位置關系的客觀事實.

(本環節設計意圖是:主要培養學生的類比思想,觀察分析發現的能力.通過合作交流、自主評價,改進學生的學習方式及學習質量,激發學生的興趣,喚起他們的好奇心與求知欲,點燃學生智慧的火花,使學生積極思維,勇于探索,主動地去獲取知識.)

通過自己的親身體驗總結一下圓一圓的位置關系.具體一點,還能不能再細分一下?(預計學生會總結出兩圓的位置關系有:相離、相交、相切3種)從而得到兩圓的5種位置關系:外離、內含、相交、外切、內切.

師:若兩圓的半徑相等,那么這樣的兩圓是否也存在上面的5種位置關系呢?

學生在對相交這種位置關系產生質疑時,教師可給予提示、引導、幫助、總結.讓學生在猜想與探究的過程中,體驗成功的快樂,培養他們主動參與、合作的意識,勇于創新和實踐的科學精神.

三、總結判定兩圓的位置關系的方法

師:思考一下,如何判定兩個圓的位置關系呢?

教師利用課件展示兩圓位置關系與兩圓圓心距和兩圓半徑的大小關系.

圓與圓的位置關系從圖形到概念再到交點個數和d與R與r的數量關系總結.

判定兩圓的位置關系的方法:

1.兩圓公共點的個數.

2.根據圓心距和兩圓半徑的大小關系.

師:兩個圓的位置關系會有第6種情況嗎?兩個圓的公共點會有3個嗎?為什么?

練習:

1.看誰答得快:

兩圓有兩個交點,則兩圓的位置關系是 ,兩圓沒有交點,則兩圓的位置關系是 ,兩圓只有一個交點,則兩圓的位置關系是 .

2.當兩圓外切,O₁O₂= 10,r₁=4時,r₂= ;當兩圓內切,O₁O₂=2,r₁=5時,r₂= .

3.定圓O的半徑是4厘米,動圓P的半徑是1厘米.(1)設⊙P和⊙O相外切,那么點P與點O的距離是多少?點P可以在什么樣的線上移動?(2)設⊙P和⊙O相內切,情況怎樣?

四、相切兩圓性質的探究

我們知道,圓是軸對稱圖形. 兩個圓是否也組成一個軸對稱圖形呢?如果是軸對稱圖形,那么它的對稱軸是什么?

1.在紙上選取外切、內切兩個圖形,分別連接兩個圓的圓心所在的直線.

2.沿著圓心所在的直線對折一下,你發現了什么? 從中得出了什么結論?

3.它的對稱軸是什么?

4.除了圓心外,有沒有特殊點在兩圓的連心上?你能說出理由嗎?

學生自行探究,教師深入指導.最后教師利用多媒體課件形象的演示兩圓相切的對稱性.

結論1:兩個相切圓組成軸對稱圖形,對稱軸是兩圓連心線.

2:當兩圓相切時,切點一定在兩圓連心線上.

(在經歷“觀察——猜測——探索——驗證——運用”的過程,滲透了從“形”到“數”和從“數”到“形”的轉化,培養了學生的轉化、思維能力.實現了感性到理性的升華,凸現數學學習的本質,“數形結合”等數學思想.本環節設計意圖是:讓學生進一步理解性質與判定,培養學生數形結合的思想,通過定理的形象記法減輕學生的學習負擔.另外,通過對例題改造,培養學生的運用意識,提高解決實際問題的能力.)

五、例題精析

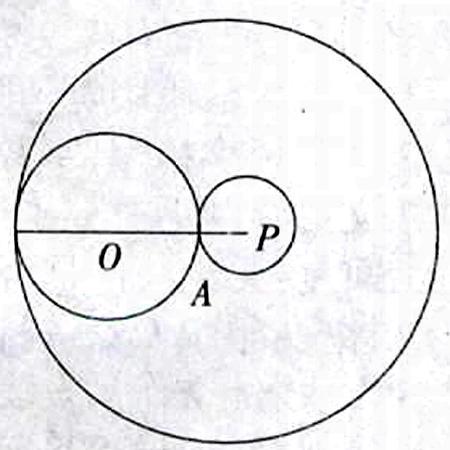
例1:如下圖,⊙O的半徑為5cm,點P是⊙O外一點,OP=8cm,求:(1)以P為圓心,作⊙P與⊙O外切,小圓P的半徑是多少?(2)以P為圓心,作⊙P與⊙O內切,大圓P的半徑是多少?

(教師引導學生自行分析,并板演解題過程.)

例2:兩個同樣大小的肥皂泡黏在一起,其剖面如下圖所示(點O₁、O₂是圓心),分隔兩個肥皂泡的肥皂膜PQ成一條直線(線段PQ稱為兩圓的公共弦),TP,NP分別為兩圓的切線.

(1)上圖中兩圓的位置關是;

(2)求∠TPN的度數?你是怎么想的?可以獨立完成嗎?

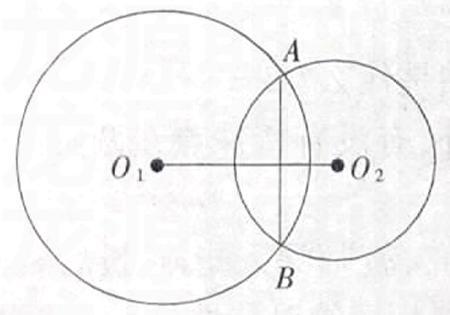
(3)O₁O₂與PQ有什么位置關系?一般情況下的兩圓相交,(如下圖)O₁O₂與AB又有什么位置關系?你發現了什么結論?

(解決生活實例問題,創設了生活情境,提供了探索的平臺,為學生創新能力的培養奠定了良好的基礎.)

結論:相交兩圓的連心線垂直平分兩圓的公共弦.

例3:兩個圓的半徑的比為2∶3 ,內切時圓心距等于 8cm,那么這兩圓相交時,圓心距d的取值范圍是多少?

(通過開放性習題解決部分學生“吃不飽”的問題.讓每個學生都得到最大的發展.)

六、引導小結

本節課你學到了哪些知識?你運用了怎樣的方法來獲得這些知識?

出示本節課的收獲對本節課的內容進行知識上的梳理.展示兩圓5種位置關系中兩圓半徑與圓心距的數量關系表格.

(小結環節的設計,目的是讓學生在學完這節課之后,對這節課進行一下反思,從而養成反思歸納的好習慣.)

七、教師寄語

兩圓位置有5種,

內外相交切含離.

切點必在連心線,

性質判定合一體.

圓的相切、相交的位置情況中,弦心距、半徑、弦常會構成直角三角形,因此有關兩圓的問題,往往可化為等腰三角形或直角三角形的問題來解決,對這種“轉化”的思想,同學們要高度重視才行呀!

(教師寄語,是通過口訣的形式,將本節課的知識點概括出來,便于學生記憶.)

【教學反思】

“數學課程標準”指出了自主探究、動手實踐、合作交流的學習方式.為了落實課程標準,在課堂教學中充分發揮學生主觀能動性,我采用動態教學法,用自己的情感去感染學生,以情感人,以情動人,以情育人,真正打動學生,熱情洋溢,以達到提高教學質量的目的.課堂教學中,我努力讓學生以認真的態度在輕松氣氛中學習知識,掌握知識,這是一種享受.從而使學生樂于學習,變被動為主動.

E-mail:hit790205@163.com

編輯/張燁