高一數學與初中數學銜接中的障礙分析與教學對策

馬自國

高一是數學學習的一個關鍵時期.但由于學生升入高中后,不適應高中數學的教學,相當多的學生數學成績不理想,出現嚴重的學習障礙,甚至對學習失去信心,導致兩極分化.本文著重分析了高一數學學習中存在的障礙,并結合實踐提出了教學對策,希望能對廣大高中數學教師有一定的幫助.

一、當前高一數學學習中存在的障礙分析

1.高中數學與初中數學特點的變化.

數學語言在抽象程度上突變.不少學生反映,集合、映射等概念難以理解,覺得離生活很遠.確實,初、高中的數學語言有著顯著的區別.初中數學主要是以形象、通俗的語言方式進行表達.而高一數學一下子就觸及抽象的集合語言、邏輯運算語言以及以后要學習到的函數語言、空間立體幾何等.

思維方法向理性層次躍遷.高一學生產生數學學習障礙的另一個原因是高中數學思維方法與初中階段大不相同.初中階段,很多老師為學生建立了統一的思維模式,如解方程分幾步,因式分解先看什么,再看什么,即使是思維非常靈活的平面幾何問題,也對線段相等、角相等.分別確定了各自的思維套路.因此,初中學習中習慣于這種機械的、便于操作的定勢方式.而高中數學在思維形式上產生了很大的變化,數學語言的抽象化對思維能力提出了更高的要求.這種能力要求的突變使很多高一新生感到不適應,故而導致數學成績下降.

知識內容的整體數量劇增.高中數學與初中數學又一個明顯的不同是知識內容的“量”上急劇增加了,單位時間內接受知識信息的量與初中相比增加了許多,輔助練習、消化的課時相應地減少了.這就要求第一,要做好課后的復習工作,記牢大量的知識;第二,要理解掌握好新舊知識的內在聯系,使新知識順利地同化于原有知識結構之中;第三,因知識教學多以零星積累的方式進行的,當知識信息量過大時,其記憶效果不會很好.因此要學會對知識結構進行及時的梳理.如表格化,使知識結構一目了然;類別化,由一例到一類,由一類到多類,由多類再到統一,使幾類問題同構于同一知識方法;第四,要多做總結、歸類,建立主體的知識結構網絡.

2.學生不良的學習狀態.

學習上存在著嚴重的依賴心理.許多學生進入高中后,還像初中那樣,有很強的依賴心理,跟隨老師慣性運轉,沒有掌握學習的主動權.表現在不制定計劃,坐等上課,課前沒有預習,對老師要上課的內容不了解,上課忙于記筆記,沒聽到“門道”.

缺乏學習興趣、學習意志薄弱.與初中階段的學習相比,高中數學難度加深,教學方式的變化較大,教師輔導時間相對減少,學生學習的獨立性增強.因此,在初、高中銜接過程中有的學生適應性強,有的學生適應性差,表現出學習情感脆弱、意志不夠堅強,遇到困難和挫折就退縮甚至喪失信心,從而導致學習成績下降.

學不得法.老師上課一般都要講清知識的來龍去脈,剖析概念的內涵,分析重點、難點,突出思想方法.而一部分學生上課沒能專心聽課,對要點沒聽到或聽不全,筆記記了一大本,問題也有一大堆,課后又不能及時鞏固、總結、尋找知識間的聯系,就造成了連續學習過程中的薄弱環節,跟不上集體學習的進程,導致數學成績的兩極分化.

進一步學習條件不具備.高中數學與初中數學相比,知識的深度、廣度,能力要求都是一次飛躍.這就要求必須掌握基礎知識與技能為進一步學習作好準備.高中數學很多地方難度大、方法新、分析能力要求高.如二次函數值的求法,實根分布與參數變量的討論,三角公式的變形與靈活運用,空間概念的形成等.有的內容還是初中教材都不講的脫節內容,如不采取措施,查缺補漏,就必然會跟不上高中學習的要求.

二、排除學生數學學習障礙的教學對策

1.教師要認真研讀“義務教育數學課程標準”和教材.

筆者認真研讀了“義務教育數學課程標準”和教材,并堅持聽初中數學課,了解初中教師的授課特點.在充分掌握了初中知識體系、初中教師授課特點、學生狀況的前提下,根據高一數學教材和“高中課程標準”的要求,及時的補充了初、高中數學的脫節內容,如立方差、立方和公式,十字因式分解法,絕對值不等式及二次函數的進一步拓展內容等,從而彌補了初、高中兩種教材銜接時出現的知識內容的斷層.

2.放慢進度,降低難度,注重教學內容和方法的銜接.

根據筆者的教學實踐,高一課時數量要增加基本概念、基礎知識的教學,教學時注意形象、直觀.要嚴格遵循學生認知發展的階段性特點,照顧到學生認知水平的個性差異.如在“集合概念”的教學中,由于集合是一個很抽象的概念,也沒有明確的定義.因此,教學中應抓住集合元素等特征,通過舉出大量的實例,讓學生從不同角度分析比較、歸納得出集合概念.再舉出一些不能構成集合的例子來進一步理解集合的概念.這樣,大量的例子不僅鞏固了集合的概念,更重要的是讓學生掌握了集合概念的內涵和外延,提煉出集合的元素的基本特征.學生不僅可以理解概念,而且能很好地應用概念——抽象的知識就“活”起來了.

3.學會構建知識體系,改進學習方法.

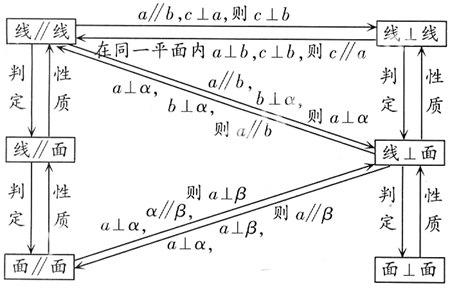
“學生的數學學習過程是用已有數學認知結構為基礎,通過同化或順應,把新知識納入到自己頭腦中的數學認知結構中的過程.在這一過程中必須使新的數學知識與已有的數學認知結構中的有關概念建立起非人為的和實質性的聯系,也就是要使學生真正理解數學知識的本質特征,掌握數學知識的內在邏輯聯系性,從而使學得的知識具有整體性和系統性”.因此,數學教學要充分揭示知識的建立、擴充和發展的過程,揭示各知識間的因果關系及本質聯系,優化學生的認知結構.比如,在學習“線面位置關系”時,師生可構建如下的知識網絡圖,使學生形成一個條理化的、排列有序的、知識間關系明確的知識體系.

4.培養學習興趣,倡導合作探究.

建構主義學習觀認為,學習者以自己的方式建構對事物的理解,不存在完全相同的理解.因此,在高一數學教學中,倡導合作探究的教學方式,通過學生間的合作探究交流,不但可以培養學生濃厚的學習興趣,而且也會使學生的理解更加豐富和全面.比如,在“函數y=Asin(?棕x+?準)的圖像及其性質”的教學中,筆者選擇了小組合作探究學習,將全班同學分成8組,由組長先把打印好以下幾個問題的卡片分給各組成員.

探究1:

1.通過觀察y=Asinx的函數圖像來研究y=sinx的圖像經過怎樣的變換可得到y=Asinx的圖像?(A>0.)

2.通過觀察y=sin?棕x的函數圖像來研究y=sinx的圖像經過怎樣的變換可得到y=sin?棕x的圖像?(?棕>0.)

3.通過觀察y=sin(?棕x+?準)的函數圖像來研究y=sinx的圖像經過怎樣的變換可得到y=sin(?棕x+?準)的圖像?

探究2:

你能用探究1中類似的方法,通過觀察記錄當A、 ?棕、?準三個參數取值變化時的圖像變化來歸納:y=sinx的圖像可以依次通過哪些變換得到y=Asin(?棕x+?準)的圖像?

首先,小組內部各成員獨立探究每一個小問題,然后將自己的研究成果在組內交流;最后在匯總本組探究成果的基礎上,每組一名代表在全班匯報交流.

前蘇聯教育家達尼洛夫說過:“教師對學生講得越多,從而留給學生獨立地獲取知識、獨立思考和進行活動提供的機會就越少,教學過程的活力和效果就越低.”在數學課堂教學中,讓每個學生通過問題探究活動,構建自己對問題的理解和解答,并在與同學或教師進行交流的基礎上,悟出對問題以及相關數學知識方法更為深刻的理解,有效地增強了學生學習數學的興趣和信心,消除了其心理障礙.

5.建立和諧師生關系,營造和諧的課堂學習氛圍.

前蘇聯偉大的理論家、教育家捷爾任斯基說過:“誰愛孩子,孩子就愛他,只有愛孩子的人,他才能教育孩子.”心理學也認為人的情感與認識過程是相聯系的,任何認識過程都伴隨著情感的傳遞.教師只有樹立科學的學生觀,構建良好的師生關系,用真誠的心去欣賞和關心每一個學生,學生才會愛戴他、才會親近他、才會“尊其師,信其道”.

總之,良好的學習狀態是學生提高學習效益的保障.新的課程理念關注對學生非智力因素的培養,尤其重視學生的學習狀態對學習的促進作用.高一是高中數學學習的起始階段,也是關鍵時期.數學教師只有充分認識到學生在學習數學中存在的諸多障礙,才能更加努力地在“備”上狠下功夫;才能使抽象知識更加“活”起來;才能使數學課堂“活”起來,使學生真切感受到數學好玩、數學有趣.“人人學有價值的數學,人人都能獲得必需的數學.”

E-mail:hit790205@163.com

編輯/張燁