物理語言的四要素

馮　源

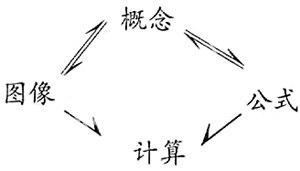
物理學家費米曾說過這樣一段話:“計算的途徑有兩種。第一種,是我所愿意采用的,即一幅清晰的圖像。第二種是有嚴格的數學架構。”雖然,他的這段話是說給另外一位物理學家聽的,但如果把這句話投射到中學物理教學上的話,似乎也頗有意義。在筆者看來,中學物理的教學過程中,應適當引導學生從語言學習的角度來學習物理,熟練掌握簡單的物理語言,以形成基本的理科思維方式。如費米所述,物理語言的核心正是“圖像”和“公式”,學生要會利用這兩種語言方式圍繞“概念”并結合“計算”闡明物理過程,解決物理問題。理科思維方式的形成過程是通過物理語言的反復運用來實現的,而“概念”,“圖像”,“公式”和“計算”正是構成中學物理語言的四要素。接下來,我們逐一剖析。

一、概念

1.概念可以是物理語言的敘述對象,也可以是形成物理語言的基本字符。由此,概念一般可分為基本型和計算型。屬于基本型的有:質點,重心,參考系,慣性,直線及曲線運動,電場,磁場等。計算型的概念有:位移,速度,加速度,摩擦力,合力,功,動能,常量(G、k)等。基本型的概念大多在于描述一個基本事實或是提供一個統一的規范,涉及一定的物理環境。計算型的概念經常是基本型概念的展開,聯系具體的物理量,可以是組成公式的基本字符,參與運算,往往具有單位,二者之關系像是電腦里的“文件夾”和“文件”,是一種結構化思維。比如直線運動就包含位移、速度、加速度、時間等具體的物理量;再如電場,圍繞其展開就有電場強度,電勢差等。基本型的概念具有概括性、整體性。而這里要特別說明的是計算型概念,它涉及細節,更具體,常用一個英文字符來簡記,即形成物理語言的每一個“字”,其目的是把定律,定理的文字描述向公式過渡。

2.拿“牛頓第一定律”來說,該節有一個要點,就是有提出把運動的概念進行細分,分成勻速運動和變速運動,前者不需要力來維持,而后者必需要力來維持。可以推測在伽利略之前的人們可能都沒有認真思考過如何對運動進行分類,所以老是對力和運動的關系問題混淆不清,甚至自相矛盾。而伽利略用他那著名的理想實驗捕捉到了唯一不需要力來維持的勻速直線運動,把這個特殊的運動形式排除以后就會發現,其他的運動都是需要有力參與的。后來牛頓明確了力、慣性、質量等概念,再借助于加速度(由伽利略定義),進而提出了牛頓第二定律。再如,學習萬有引力定律時,萬有引力和重力的異同,以及向心加速度和重力加速度的區別,都是令學生困惑的。前者要用到受力圖,后者得借助運動學公式來辨析。物理概念的建立是為了解決或闡述某個物理問題,反過來,在已建立的物理概念的基礎上又去研究新的問題,從而建立新的物理概念,這種鏈鎖式的問題解決,形成了物理概念體系。

二、圖像

1.中學物理公式并不算多,但題型多變,特別體現在圖像上。圖像能夠傳遞物理知識信息,具有交流物理意識的作用,這也對學生的想象力提出了要求。物理想象不同于文學藝術中的想象,它比文學藝術中的想象更概括、更抽象。物理想象也不同于數學想象,它不僅需要空間想象,也需要對客觀事物狀態及發展過程的較為形象的想象。圖像能成為學生思維的起點和路標,如果學生只對著問題“ 干想” 就很難打開思路,而借助圖像將擬題者設計的物理情景、物理過程復原出來,就使思維有了起點,圖畫出來了,解題的方法也有了。因為借助圖像能產生形象思維,很容易由圖像中的形象尋找到幾何關系。聯想到物理公式,再與記憶中有關的表象進行比較,找出已有的經驗,從而得到解決問題的方案。

2.針對大多數的物理習題來說,使用最普遍的莫過于受力圖、運動過程圖、電路光路圖、電磁場線圖等。而這些當中,除了電路光路圖外,其他圖大都屬于矢量圖的范疇,也是主要的難點所在,即便是它們常常被限制只能出現在二維平面中。就力學部分來講,接觸較多的有受力分析圖(力的示意圖)和運動過程圖等。比如第一章里所涉及的“力的三要素”,“重力”、“彈力”、“摩擦力”、“力的合成、分解”等是構成受力分析圖的基礎。當然,以后還有諸如電場力、磁場力等新成員加入其中。對受力分析圖來說,由于質點概念的引入,力的作用點往往都統一了,那么“力的三要素”中,力的方向和大小就顯得更為要緊,受力圖的關鍵就在于找好各力的方向(受力和施力),并判斷其是恒力還是變力。雖然不同性質的力其方向找法不盡相同,但多數情況下,各力都會平行或垂直于題設情景中的某一平面或某一連線,以它們為參考是必要的,便捷的。而在“直線運動”里出現的習題往往就畫個初始情景,甚至有的只給出文字敘述。這就要求學生能按照題設條件想象出被研究對象的大致運動過程,還有的可能包含多過程或多物體,更涉及討論,隱含條件等,想象好之后就要表達在紙上,形成草圖。在中學物理教材的大多數章節里,受力圖和運動過程圖幾乎都有伴隨(“恒定電流”等章節除外),可以說貫穿了整個中學物理的始終,是解答眾多習題的法門。而就一般中學生來說,這種想象能力的培養和訓練可謂困難重重,其重要性自是不言而喻,教學當中要盡量督促學生動起手來。當然,還有其他諸如電場圖,磁場圖,電路圖,實驗裝置圖,物理現象圖和一些用于記錄數據的圖表等,不同的圖像有著不同的用途和不同的細節,這里不多闡述。

三、公式

1.公式是物理定律,定理,以及物理概念的抽象表達,其重要性顯而易見。此外,物理定律有著令人驚訝的普適性,這也正是它吸引人的地方。曾經有人問李政道,乍一接觸物理學,有什么東西給他印象最深。他毫不遲疑地回答說,是物理法則普適性的概念深深地打動了他。我們知道,有些公式來自于實驗事實,如牛頓第二定律、歐姆定律等;有的來自于推導,如動能定理、動量定理等。教材會用最簡單的方式引入它們,但由于普適性的緣故,它們可以適用于更多、更復雜的問題,這就讓出題者擁有了幾乎無限的發揮空間。學生總是感覺看得懂教材、聽得懂講解,但真正考試的時候總是束手無策,看到答案的時候又感慨不已:原來還是關于那些基本公式的應用。這就要求學生對公式能有較高的熟練度、敏感度。熟練度可以從習題練習中得到,敏感度則是經驗的積累。公式其實就是文字語言的簡記形式,等于是構成物理語言的“句”,其中的各字符都有相應的物理意義,大多屬于計算型概念的范疇。當然,正如房子是由磚砌成,但磚并不代表房子一樣,由定律所演化出的各種公式或推導出的各類定理并非字符或概念的機械累積,而是代表著自然界的法則,宇宙的“程序”,有著客觀的內部結構。

2.對于公式的應用,僅在中學物理范疇,一個“F合=ma”似乎就具有無窮的潛力;一個動能定理也能得以橫行無忌。我們需要做到的是,清楚定律的來龍去脈以及適用范圍,掌握定理的推導過程,結合物理情景,牢記于心;然后抓準每個字符(即計算型概念)的物理意義,熟悉其常見的擴展形式。要給學生指出,公式里頭有些字符特別活躍,易出狀況,常為命題者所鐘愛。比如“F合=ma”里的“F合”和“a”,再如動能定理里的“W總”和“v0”,“vt”,單擺周期公式里的“g”和“l”等。它們常作為方程的擴展點,起著紐帶的作用,實現方程之間的“通信”,也是解題的線索。關注這些字符,可以很清楚地看到數據處理的流程,就像是在看一列面向過程的計算機程序一樣,這也是平時所謂的“解題思路”。處理一些例題的時候,要盡量把題上的方程還原回原始的公式,進而讓學生熟悉其常見的變化形式(這個過程也常涉及圖像)。在做計算題時,牽涉到很多東西,有受力分析、過程分析、隱含條件的挖掘、變量分析、特殊量的應用等等,每一個環節都需要習題來鞏固。

四、計算

1.中學物理的計算說來很基本,就無非加、減、乘、除、乘方、開方、基本函數、數列等,要強調的是,三角函數,二次函數,數列和平面幾何等數學內容滲透于物理過程是不可避免的,這也常常令學生忐忑不安,且多數時候還是在做字符運算,更是讓人心亂如麻。所以,除了熟悉基本的數學知識外,學生能盡快從數字計算過渡到字符運算也是相當重要的,這一過程尤其需要時間和精力。從物理語言角度來說,這一過程好比是在連句成“篇”,而關鍵的問題在于,該怎么個連法,即如何解方程。

2.這里需要提示學生的就是,在讀完題以后,往往第一件事情就是把已知量,特殊量和未知量等“翻譯”成字符形式,公式一但被應用到具體問題中,就形成方程,如同讀文章有時要咬文嚼字一樣,寫方程時就應該注意哪些字符是已知,哪些未知,哪些可能會在過程中被消去,對每個“字”都要“咬準”。而引入下一個方程的線索,或是方程組的求解,也往往來自于這樣的字符分析。字符方程組的求解看似復雜,實則簡單,所謂字符的運算在多數時候其實就是一種“搬運”,比如提公因式、代入消元;又或等式兩邊同乘、同除等。很顯然,在計算前作好字符分析,鎖定好未知量是解決這類計算問題的關鍵所在。

五、總結

四要素中,“圖像”和“公式”無疑是骨架結構,“概念”和“計算”起著基礎和關聯的作用,四者緊密結合,互相滲透,教學時不可孤立或只片面強調某一方面,而要注意彼此的關聯性。就這樣,匯“字”成“句”,連“句”成“篇”,再配以“圖”,即構成了基本而頗具特色的物理語言。要說明一下,在物理語言當中,除了符號語言、圖像語言外,還有就是文字,但這里并沒有把文字語言作為要素,因為它是幾乎所有學科的前提和基礎,是一個通用的平臺,而并非是物理語言的自身特點。