B 樣條曲線的等距算法及應用

朱朝艷， 陳小雕

（1. 浙江大學寧波理工學院，浙江 寧波 315100； 2. 杭州電子科技大學計算機學院，浙江 杭州 310018）

等距曲線、曲面的計算是幾何計算的一個重要問題。它除了應用于傳統的CNC 加工，還廣泛應用于CAD 中的諸如圖案設計等領域[1]。等距曲線、曲面的計算主要有兩大類方法，一種是精確的方法，另一種是近似的方法。Farouki 等人討論了可以用有理形式精確表示的曲線[2-5]。不幸的是，很多曲線的等距曲線是不能用有理形式精確表示的。在近似方法上，有很多文章討論了平面曲線的等距曲線[6-7]。主要有兩類方法，第一種是基于曲線逼近的方法[8,18]，這類方法中，或者用更加簡單曲線，如直線段或圓弧等逼近原始曲線，并借助逼近曲線的等距曲線來近似原始曲線的等距曲線，同時用來去除等距曲線的自交，降低了求交計算的復雜度，但最終得到的等距曲線的段數較多；另一種則是基于自由曲線控制點的方法[1,9-15,19-20]，這種方法得到的段數相對較少，但往往有自交情況，去除自交的計算量將隨著曲線的復雜化而變得很大。

保持等距曲線的正確的拓撲結構非常重要。在傳統的CNC 加工中，等距曲線的正確拓撲結構對于刀具的路徑設計有著決定性的作用。在圖案設計等應用中，等距曲線的不正確的拓撲結構，可能導致最終得到的雙側等距曲線或者因缺失一段曲線不封閉，或者因多出一段曲線而出現懸邊。圖1 表示了單邊等距曲線的示意圖。圖1(a)中，多出來一段，若繼續作另一邊的等距曲線，會導致出現懸邊；圖1(b)中，缺少一段，若繼續作另一邊的等距曲線，會導致雙側的等距曲線不封閉；圖1(c)中的等距曲線具有正確的拓撲結構，對應的雙側等距曲線也是封閉的。

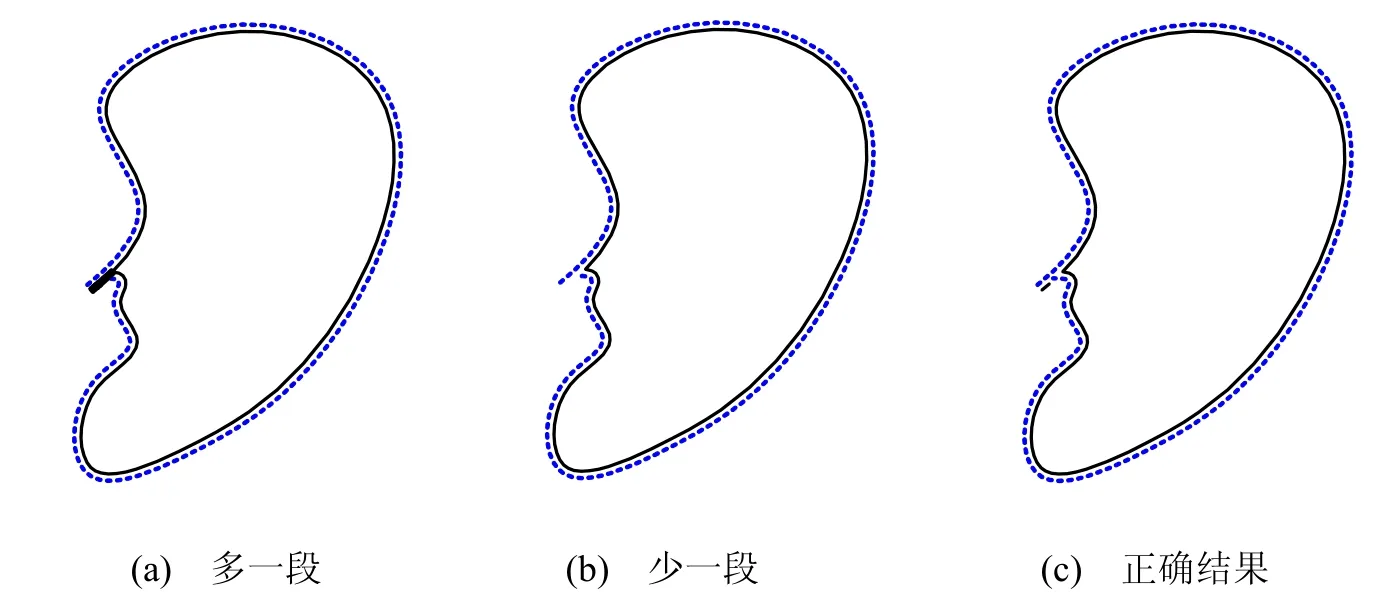
圖 1 等距曲線拓撲結構的示意圖

本文討論B樣條曲線的等距曲線的近似計算方法。首先，用雙圓弧逼近的原始曲線的等距曲線，同時提出了基于單調圓序列的方法來計算等距曲線的近似自交點，并以此為初值迭代到精確的自交點。其次，根據前面計算的自交點作為等距曲線上的關鍵分段點并進行各個分段曲線的取舍。最后，應用文獻[14-15]中的方法計算各個分段的等距曲線，同時保持段與段之間的拓撲關系，得到最終的等距曲線。本文方法得到的等距曲線可以保持正確的拓撲結構，最后得到的B樣條表示的等距曲線具有較少的控制點。

1 求解B 樣條曲線的等距曲線

一般的n 次B 樣條曲線可以表示為

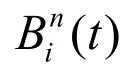
其中 )(tN 為曲線 )(tC 在參數t 處的單位法 向。一般地，n 次B 樣條的等距曲線不再是n 次B 樣條，甚至不能精確地表示為有理形式，人們 通常用近似的方法求解原始曲線 )(tC 的近似等 距曲線。在CNC 加工中，要求刀具在行進的過程中避免干涉，它所要求的結果等距曲線就是由式子(2)確定的等距曲線上，所有到原始曲線的最近距離恰好等于有向等距距離d 的絕對值的點的集合

其中 Dis ( Rd(t)，C)表示點 Rd(t)到曲線C 的最近距離。這種應用下，僅僅去除單側自交點，可能會或增加或減少等距曲線段（見圖1）。本文的算法專門針對式子(3)確定的應用，是對原先等距方法的補充。不失一般性，下面只考慮d＞0的情況，d＜0的情況可以同樣處理。

1.1 樣條曲線的自適應離散采樣

在實際應用中，樣條曲線的自適應離散采樣，可以采用基于曲率的方法[1]。本文用雙圓弧逼近的方法直接對相應的等距曲線進行自適應離散采樣。實踐表明，在給定的精度下，基于圓弧逼近的離散方法，得到的采樣點數目往往要少于基于折線段逼近離散的方法。本文采用的雙圓弧逼近的方法，主要參考了Yang[16]的算法。實踐證明，雙圓弧求交得到的近似交點，比用折線段求交得到的交點，更為接近原始曲線的精確交點；基于雙圓弧離散的方法得到的等距曲線上的近似自交點比基于折線段離散的方法得到的相應的近似自交點具有更高的精度。

1.2 等距曲線的關鍵段點的定位與分段的取舍

由上文提及的等距曲線的概念容易得知，最后得到的去掉自交后的結果等距曲線是由若干段連續的曲線組成。為了方便起見，本文稱各段 結果等距曲線段的端點為段點，并記χ 為結果等距曲線的所有段點的集合，+μ 為原始曲線的正向等距曲線，?μ 為原始曲線的負向等距曲線，+Ω 為+μ 的所有自交點的集合，?Ω 為所有+μ 與?μ 交點的集合，并記 Ω = Ω+∪Ω?。

定理1 ∈χ Ω 。

根據定理1，求出Ω 對應的分劃A，并由此決定由A 確定的每一個小區間的取舍，最后得到的，就是結果等距曲線（段）對應在原始曲線的若干個參數小區間，并且這些小區間對應的等距曲線，不存在自交的現象，可以用已有的各種方法去求解。

首先討論關鍵段點的定位，并由此得到Ω 對應的分劃A。這個過程就是求解所有的交點集合Ω 。直接應用等距曲線之間求交，一般比較 費時間。利用逼近等距曲線后得到的雙圓弧序列來估計交點，可以降低求交計算的復雜度與計算量，同時，得到交點比折線段方法更加接近精確的交點。

本文應用單調列技術消除圓弧序列的自交問題，并應用包圍盒等技術來求解兩列圓弧序列之間的交。首先，分別依次取所有控制點坐標的x 分量與y 分量，得到兩個坐標序列，根據每列相鄰坐標分量的差組成的數列的變號數，選擇變號數小的，不妨設該坐標分量為x 分量。然后，對每段雙圓弧增加點，使得每一段簡單圓弧都是 關于該坐標分量單調。依次選擇連續的多個圓弧組成的，關于x 分量單調的子序列，作為一個單調列，這樣可以得到若干個單調列，并且每一個單調列內的圓弧，兩兩不相交。

確定分劃A 之后，就需要確定小區間的取舍。小區間的準確取舍，對于最后等距曲線的拓撲結構是至關重要的。等距曲線上相鄰兩段單調列的交點，利用向量點積判斷的方法，速度很快，可以用來去除局部環（如圖2）。但是，該方法去除全局環，效率是不夠的，容易發生誤判。利用求解點到逼近折線段，或者點到逼近圓弧的距離，常因為段數的影響速度變得比較慢，而且由于逼近的誤差，在臨界狀態下也容易發生誤判，特別的，當所取的點不在精確等距曲線上的時候，誤判幾率更大。本文綜合了上述這兩種方法的優點進行了判斷處理。首先，利用向量點積的判斷方法，排除到原始曲線距離明顯小于等距距離的小區間。在余下的區間，選取相鄰兩個交點所確定的小區間內的精確等距曲線上的點作為基準點，來求解點到原始曲線的距離，避免了逼近誤差引發的臨界問題。基準點的選取，可以分為兩種情況，如果相鄰的交點分別屬于不同序號的雙圓弧，則直接選取兩個交點之間的雙圓弧的端點作為基準點；否則，取兩交點對應的參數的中間值對應在精確等距曲線上的點，作為基準點。然后，計算基準點到原始曲線的最近距離，如果距離在容差的范圍內等于d，則保留，否則舍去該小區間。

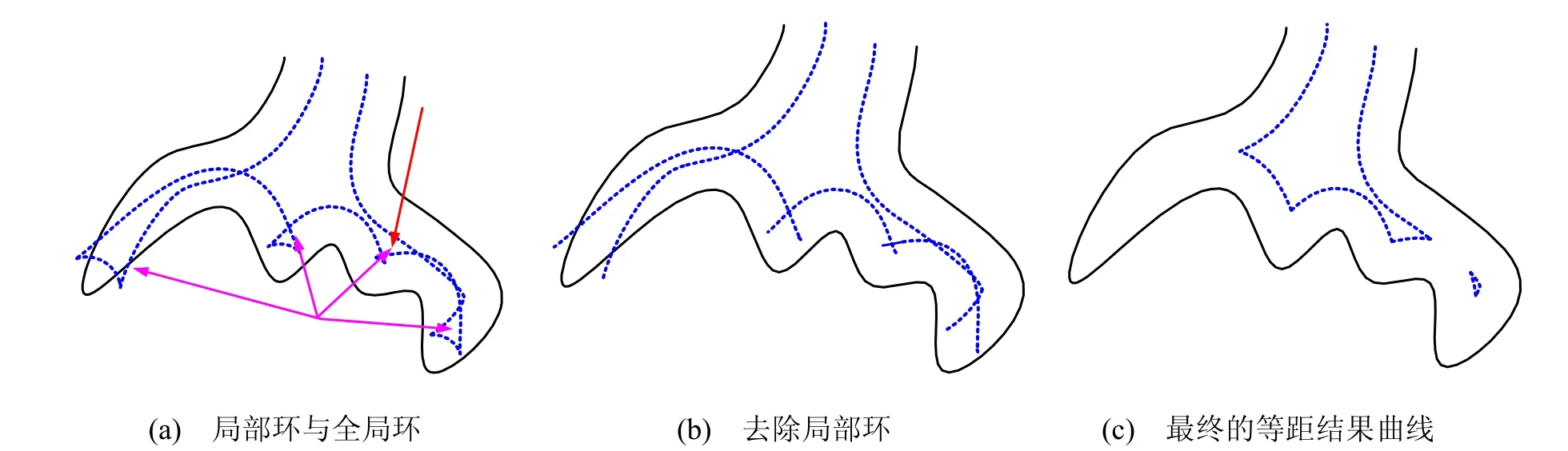
圖2 局部環與全局環處理結果

一般的，可以用雙側等距曲線的封閉性來幫助檢驗等距曲線的拓撲穩定性。圖3 是一個樣條曲線雙側等距的實例, 其中，3(a)是原始曲線，3(b)是AutoCAD 軟件局部放大的結果，3(c)是OpenCAD 軟件局部放大的結果。可以看出，本文的方法的結果，有更好的拓撲穩定性。當自交點的參數估計沒收斂到精確自交點（實例中沒出現這樣的情況），圖4 演示的本文的閉合處理方法也能保證最后得到的雙側等距曲線是閉合的。

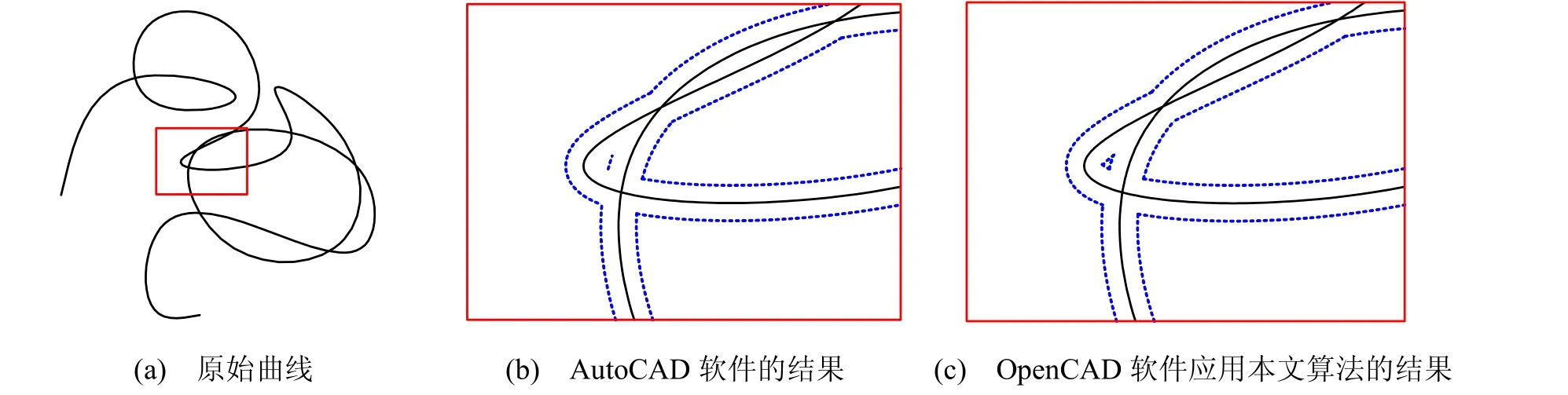
圖3 取舍的實例與比較

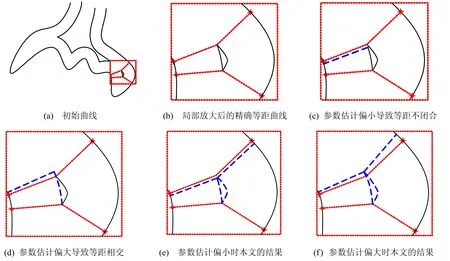
圖4 閉合處理方法的比較

1.3 各個分段的等距曲線的最后處理

最后結果樣條的處理上，可以直接用三次樣條插值前面得到的采樣點。這種方法的好處，結果曲線比較簡單，在精度范圍內也能保證插值后各段樣條之間兩兩不相交，同時還能在全局交點處能保持連續，這種算法可以應用于圖案設計。一般地，前面離散過程中得到的采樣點數目可能比較大，有時候由于精度等原因，甚至還需要對采樣點進行加密，相應的，最后結果樣條的段數比較多，這是工程應用上的一大忌諱。直接用基于控制點調整的方法，對估計出來的小區間作等距曲線，段數相對來說少一些，但是不能保證插值后各段樣條之間兩兩不相交，特別地，在全局交點處還可能不連續，這種情況的一個直接表現是繼續作另外一側的等距曲線，兩側等距曲線在原本應該閉合的情況下，不能閉合（見圖4）。用求交的方法可以處理相交的情況，但是比較耗時間；Lee[8]針對參數小區間端點的參數值迭代求精的方法，在一定程度上可以改善，但是它依賴于迭代算法收斂的具體狀況。

本文的處理方法，應用類似Yang[17]的基于控制點調整的逼近方法，對上面估計得到的參數小區間，直接求解等距曲線的逼近曲線。如圖4所示，它預先指定了每一段逼近曲線的端點，就是上面求解得到的交點，這樣，減少了段數，同時也避免了在全局交點處可能不連續的情況，可以同時應用于圖案設計與CNC 等多種工程應用。

2 實例與結論

將本文的算法應用到商業軟件OpenCAD中，并用 3 個實例與同類的國外著名軟件AutoCAD2004, AutoCAD2005 就樣條曲線的雙側等距功能作比較。為方便起見，分別將AutoCAD2004，AutoCAD2005 以及OpenCAD 分別得到的3 個結果簡稱為結果A2，A4與B。

例1 圖5是針對閉合的，自交的曲線進行雙側等距的結果比較，結果A2, A4分別給出部分等距，B給出了所有的等距曲線段，在視覺上具有更好的美感。曲線為三次樣條曲線，控制點與節點向量分別為：(456.2347,218.4149)(449.6793,295.0248) (577.9684,484.1168) (964.6972,235.6098) (479.0472,178.5197) (584.1964, 515.6817) (855.0988,486.1700) (996.1325,252.3531) (727.8244,37.1056) (666.6469,449.5623) (1117.0048,489.0262) (1047.2378,-13.7901) (646.8361,-10.8984) (462.4325,145.9829) (456.2347,218.4149)與 {0.0,0.0,0.0,0.0, 230.6695, 474.8459,725.8914, 924.3524,1158.021,1381.021,1572.056,1809.599, 2095.662,2406.339,2813.724,3031.814,3031.814, 3031.814,3031.814}。等距偏移量為20。

圖5 閉合自交曲線雙側等距結果曲線比較

例2 圖6是針對開的，自交的曲線進行雙側等距的結果比較，結果A2, A4均漏掉了一段等距曲線段，B給出所有了的等距曲線段。曲線為三次樣條曲線，控制點與節點向量分別為：

(744.1808,508.8816) (776.7853,617.1998)

(833.3231,805.0285) (1078.0127,477.1051)

(648.0156,613.3402) (904.6993,768.0031)

(1050.8365,683.1869)(1053.8494,416.9693)

(692.1974,641.8598) (1057.0341,807.6433)

(1130.0377,608.4000) (1146.8524,404.0772)

(905.6308,403.5530) (881.9587,626.8380)

(1034.5717,575.1042) (1005.0188,465.7295)

(851.9888,419.3761) (794.0705,602.0181)

(925.0642,738.1799) (708.6746,770.5750)

(679.8814,704.0337) (674.9950,692.7413)與

{0.0,0.0,0.0,0.0,232.64907,403.42409,621.36462,

795.97228,929.19622,1091.2253,1307.7149,

1555.8348,1688.0376,1878.5677,2042.7598,

2179.7761,2274.3395,2341.8718,2459.9235,

2639.7297,2725.5404,2902.8505,2939.0912,

2939.0912,2939.0912,2939.0912}。等距距離為20。

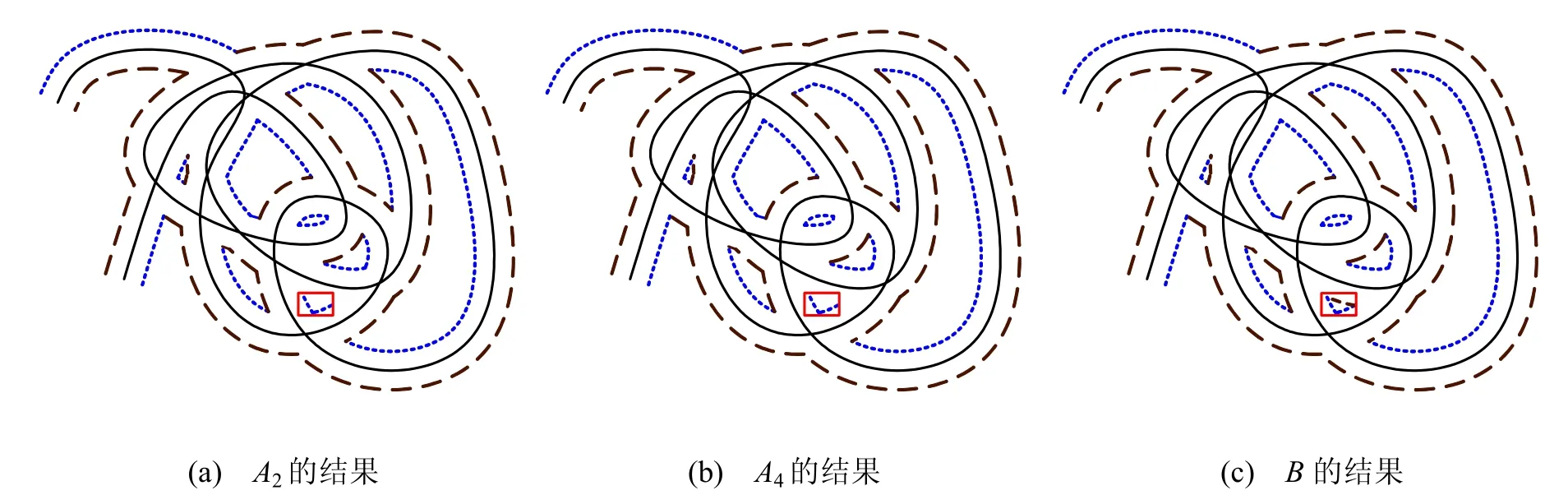
圖6 開自交曲線雙側等距結果曲線比較

例3 利用例2 中的數據，選取其中兩段等距曲線段進行控制點數目比較，結果A2, A4得到兩段等距曲線段的控制點數目分別為68 與74，結果B 得到的數目分別為14 與16（見圖7）。

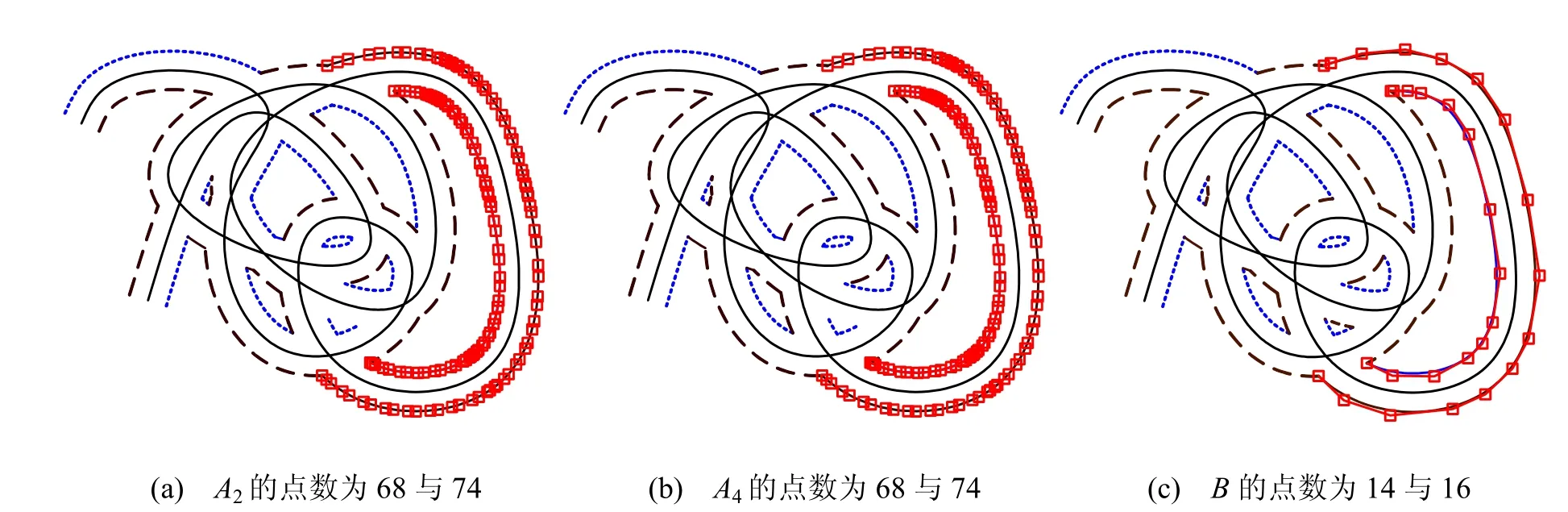
圖7 兩段等距曲線段控制點數目比較

本文討論了B 樣條曲線的等距算法，提出了基于雙圓弧逼近和單調圓序列技術的自交消除算法，同時綜合了基于控制點調整的曲線逼近等技術，并在此基礎上提出了一種關于B 樣條曲線的統一的、魯棒的等距算法。本文的算法具有保持拓撲穩定，以及生成的等距曲線段數較少等特點。它已應用于商業軟件OpenCAD 中，適用于處理自交，閉合等任意類型的樣條曲線的等距，它還可以應用于圖案設計等領域。實例也表明了本文的算法結果可以具有更精確的拓撲結構和較少的段數。

[1] Piegl L, Tiller W. Computing offsets of nurbs curves and surfaces [J]. Computer-Aided Design, 1999, 31： 147-156.

[2] Farouki R T, Neff C A. Analytic properties of plane offset curves [J]. Computer Aided Geometric Design, 1990, 7(1-4)： 83-99.

[3] Farouki R T, Neff C A. Algebraic properties of plane offset curves [J]. Computer Aided Geometric Design, 1990, 7(1-4)： 101-127.

[4] Farouki R T, Sederberg T W. Analysis of the offset to a parabola [J]. Computer Aided Geometric Design, 1995, 12(6)： 639-645.

[5] Pottmann H. Rational curves and surfaces with rational offsets [J]. Computer Aided Geometric Design, 1995, 12： 175-192.

[6] Pham B. Offset curves and surfaces： A brief survey [J]. Computer-Aided Design, 1992, 24(4)： 223-229.

[7] Maekawa T. An overview of offset curves and surfaces [J]. Computer-Aided Design, 1999, 31： 165-173.

[8] Lee I K, Kim M S, Elber G. Planar curve offset based on circle approximation [J]. Computer-Aided Design, 1996, 28(8)： 617-630.

[9] Hoschek J. Spline approximation of offset curves [J]. Computer Aided Geometric Design, 1988, 5(1)： 33-40.

[10] Meek D S, Walton D J. Offset curves of clothoidal splines [J]. Computer-Aided Design, 1990, 22(4)： 199-201.

[11] Sederberg T W, Buehler D B. Offsets of polynomial Bezier curves： Hermite approximation with error bounds [C]//Lyche T, Schumaker L L, editors. Mathematical Methods in Computer Aided Geometric Design, Volume II, Academic Press, 1992： 549-558.

[12] Coquillart S. Computing offsets of B-spline curves [J]. Computer-Aided Design, 1987, 19(6)： 305-309.

[13] Klass R. An offset spline approximation for plane cubic splines [J]. Computer-Aided Design, 1993, 25(5)： 297-299.

[14] Kumar R, Shastry K G, Prakash B G. Computing constant offsets of a NURBS B-Rep [J]. Computer-Aided Design, 2003, 35： 935-944.

[15] Tiller W, Hanson E G. Offsets of two-dimensional profiles [J]. IEEE Computer Graphics and Applications, 1984, 4(9)： 36-46.

[16] Yang X N. Efficient circular arc interpolation based on active tolerance control [J]. Computer-Aided Design, 2002, 34： 1037-1046.

[17] Yang H P, Wang W P, Sun J G. Control point adjustment for B-spline curve approximation [J]. Computer-Aided Design, 2004, 36(7)： 639-652.

[18] 汪國平, 孫家廣. 平面NURBS 曲線及其Offset 的雙圓弧逼近[J]. 軟件學報, 2000, 11(10)： 1368-1374.

[19] 劉利剛, 王國瑾. 基于控制頂點偏移的等距曲線最優逼近[J]. 軟件學報, 2002, 13(3)： 398-403.

[20] 汪國平, 陳玉健, 孫家廣. 基于控制頂點擾動的平面Offset 曲線的NURBS 逼近[J]. 計算機學報, 1999, 22(12)： 59-66.