消除零級衍射和循環移位改善計算機合成 全息圖的再現質量
劉 敏, 楊光臨, 謝海燕
(1. 北京大學區域光纖通信網與新型光通信系統國家重點實驗室,北京 100871; 2. 中科專利商標代理有限責任公司,北京 100083)
本文針對計算機合成全息圖再現象質量問題[1],分析了影響再現象質量的主要因素,并提出了一種能有效改善合成全息圖再現象質量的方法。
采用數字圖像去計算合成全息圖,在信息安全方面有著廣泛應用,如,數字全息水印技術[2-7]。但是,其再現理論,基本上都是從光學理論直接借鑒過來的,是基于模擬域。而采用數字圖像去合成全息圖的制作和再現都是用計算機處理的,完全建立在數字域。數字域和模擬域的理論雖然相似,但是,不能完全等同。例如,光信息處理中連續兩個透鏡的作用等同于成倒立虛像,但計算機處理中數字圖像經過連續兩次離散傅里葉變換得到的是原圖像的上下左右顛倒的虛像,并且有一行和一列的循環移位(圖1(b))。可見,在數字域從理論上分析合成全息圖的再現情況是必要的,而且很有用處。
本文在得到Burch 型合成全息圖再現的數學表達式后,利用計算機處理的靈活性,調整虛像的像素位置消除循環移位,同時,消除再現的零級衍射,從而不需要通過取對數來顯示再現象,使得Burch 型合成全息圖能夠精確恢復原圖像。
1 Burch 型合成全息圖原理
根據Burch 型合成全息圖的原理[6],其合成全息圖的透過率函數為

這里 ( , )B x y 是物函數振幅函數的歸一化結果,α表示參考光的載頻。
根據空間帶寬積的要求,Burch 型合成全息 圖的傅里葉抽樣數 M=β1m, N = β2n必須滿足

m、n 是原數字圖像的像素大小。
2 Burch 型合成全息的再現原理
為了模擬光學全息中毛玻璃的漫散射特性,數字圖像 ( , )I p q 在傅里葉變換前乘以隨機位相rand ( p, q) ∈ (0,1),得到 I ′( p, q) = I ( p, q) ej?2π?rand(p,q), I ( p , q )的傅里葉合成全息圖記錄的是 I ′( p, q)的傅里葉變換譜,即
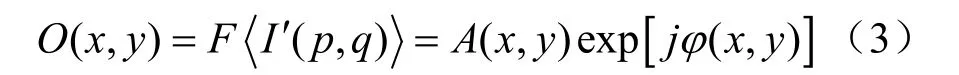
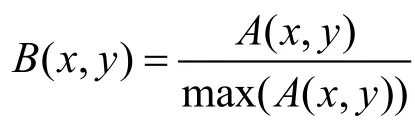
由式(1)可以得到
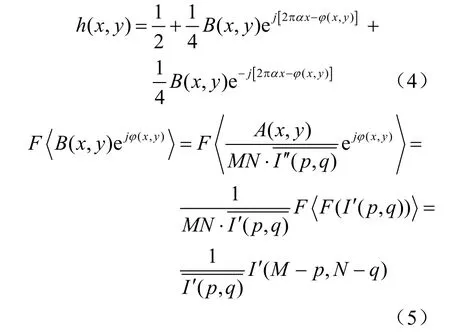
考慮到傅里葉變換與其反變換的關系,有
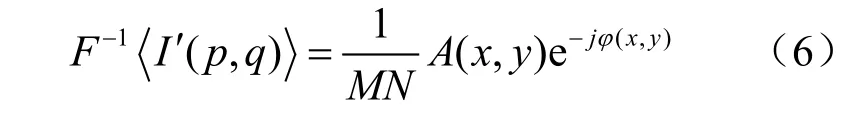
那么
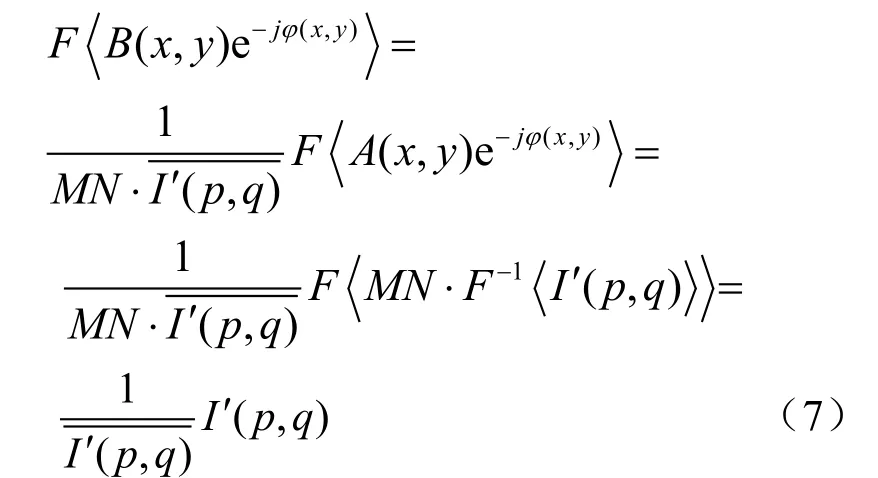
那么

MN ?δ (1,1)不是嚴格意義上的沖擊函數,這里表示只在點(1,1)有值。
雖然上式中后兩項都是復數,但只要保證它們在再現平面上不會交疊,就可以分別對三項取模,

圖 1 連續兩次DFT的循環移位作用
于是上式可以化簡得
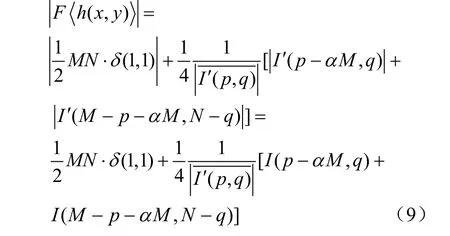
3 實驗分析
3.1 離散傅里葉變換產生循環移位
根據二維離散傅里葉變換的性質,若對數字圖像 ( , )I p q 的傅里葉變換的抽樣單元數為M N× ,則
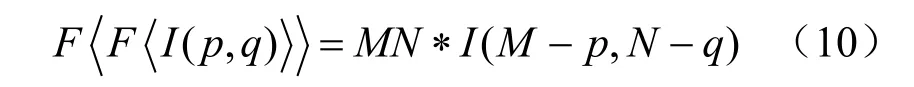
在光學全息中,透鏡的作用相當于傅里葉變換,連續兩次DFT 的作用相當于經過兩次光學透鏡作用后成倒立虛像。但是,需要指出的是,由于DFT 的循環移位作用,使得虛像的最后一行和最后一列被分別循環移位到第一行和第一列。從圖1(b)的被圈出來的區域:最左邊的黑線以及最上邊的黑色區域可以看到循環移位的存在,這正是圖1(a)虛像的最后一行和最后一列分別循環移位到第一行和第一列的結果。
3.2 消除零級衍射和循環移位再現象
MN ?δ (1,1)是冗余信息,對再 現象沒有貢獻,且嚴重降低了再現圖像的對比度,因此將它去掉得到下式
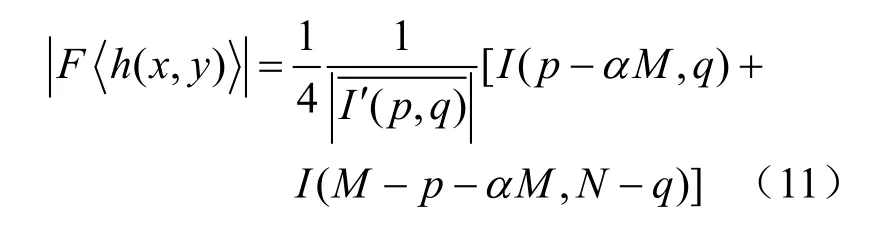
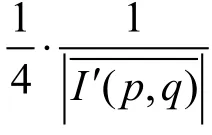
消除零級衍射后,再通過調整再現虛像的像素位置消除循環移位,使得Burch 型合成全息能精確恢復原圖像。
圖2 是抽樣倍數 β1= 2, β2=2的全息圖2(a) 及常規再現圖2(b)的情況,圖2 (b)的頂端就是很明顯的循環移位;通過去掉零級衍射后得到圖3 (a),其中間有很明顯的循環移位,于是通過調整像素位置消除循環移位后得到圖3(b),Burch 型合成全息圖再現得到精確的實像和虛像。
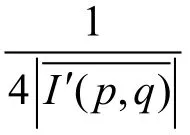

圖 2 合成全息圖和傳統再現圖像

圖 3 消除零級衍射和循環移位改善再現質量圖像

表1 對應像素位置像素值的比值
4 結 論
本文在數字域推導了采用數字圖像去合成Burch 型全息圖的再現表達式,指出了影響再現質量的兩個因素,一是零級衍射作為冗余量嚴重降低了再現象的對比度,另一個原因是連續兩次DFT 變換使得再現的虛像產生一行和一列的循環移位。于是,通過調整虛像像素的位置消除循環移位和消除零級衍射,有效地提高了再現象的對比度,理論和實驗都證明了,這種方法能夠使得Burch 算法精確地恢復原圖像。本文提出的再現方法也同樣能夠有效地提高黃氏和李威漢型合成全息圖再現象的質量。
[1] Yang Guanglin, Xie Haiyan. An approach compress information of computer-synthesis hologram with shape adaptive binary tree predictive coding and fast Fourier transform technique [J]. IEEJ Trans. EIS. , 2005, 125(1): 99-105.
[2] Nobukatsu Takai, Yuto Mifune. Digital watermarking by a holographic technique [J]. Appl. Opt., 2002, 41(5): 865-873.
[3] Yoshinao Aoki. Watermarking technique using computer-generated holograms [J]. Electron. Commun. Japan 3, 2001, 84(1): 21-31.
[4] Hsuan T Chang, Chung L Tsan. Image watermarking by use of digital holography embedded in the discrete-cosine-transform domain [J]. Appl. Opt., 2005, 44(29): 6211-6219.
[5] Smirnov M V. Holographic approach to embedding hidden watermarks in a photographic image [J]. J. Opt. Technol., 2005, 72(6): 464-468.
[6] Burch J J. A computer algorithm for synthesis of spatial frequency filters [C]//Proc. IEEE, 1967, 55: 599-601.
[7] Liu Min, Yang Guanglin, Xie Haiyan, et al. Computer-generated hologram watermarking resilient to rotation and scaling [J]. Opt. Eng., 2007, 46(6): 060501-060503.

