三元多項(xiàng)式微分系統(tǒng)的反射函數(shù)與周期解

周 堅(jiān),趙士銀

(宿遷學(xué)院教師教育系,江蘇宿遷 223800)

0 引 言

一般情況下,研究客觀世界中許多物體的運(yùn)動(dòng)規(guī)律可歸結(jié)為研究微分系統(tǒng),

解的性態(tài).若系統(tǒng)(1)為特殊的周期系統(tǒng),即 X(t+ 2ω,x)= X(t,x),(ω＞0,(t,x)∈R1+n),其解的性態(tài)的研究可借助 Poincare′映射[1-3].但對(duì)于一些不可積系統(tǒng),尋找其 Poincare′映射往往很困難. 1980年,Mironenko建立了反射函數(shù)這一嶄新的理論,該方法的好處在于,即使系統(tǒng)(1)為不可積系統(tǒng),也能通過反射函數(shù)法來建立其 Poincare′映射[4-12],從而達(dá)到研究周期系統(tǒng)解的性態(tài)的目的.利用反射函數(shù)理論研究微分系統(tǒng)解的性態(tài)是一個(gè)嶄新的課題,有許多問題值得研究.本文就其中之一進(jìn)行研究,并得到了一些全新的結(jié)論.該結(jié)論為進(jìn)一步解釋一些物體的復(fù)雜運(yùn)動(dòng)規(guī)律提供了新的判定準(zhǔn)則.

1 引 理

考慮微分系統(tǒng)(1)滿足:X(t,x)連續(xù)可微,且對(duì) ?(t,x)∈R1+n,其 Cauchy問題具有唯一解t|→φ(t;τ,x),t∈I?R.

定義1[4]稱連續(xù)可微函數(shù) F(t,x)=φ(-t; t,x),(t,x)∈D為微分系統(tǒng)(1)的反射函數(shù).

由文獻(xiàn)[4]知,函數(shù) F(t,x)為系統(tǒng)(1)的反射函數(shù)的充要條件為它是偏微分方程,

的解.

引理1 若 X(t+2ω,x)=X(t,x),系統(tǒng)(1)的解由其初值唯一確定,F(t,x)為系統(tǒng)(1)的反射函數(shù),則系統(tǒng)(1)的 Poincare′映射可定義為,

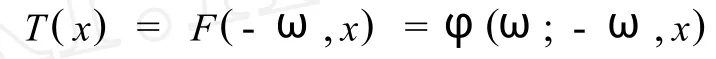
從而系統(tǒng)(1)在[-ω,ω]上有定義的解φ(t;-ω, x)為2ω-周期解當(dāng)且僅當(dāng) x為方程F(-ω,x)= x的解.

2 主要結(jié)論

考慮三元多項(xiàng)式微分系統(tǒng),

其中:

ai= ai(t),bi=bi(t),ci=ci(t)為 R上的連續(xù)可微函數(shù),且 a—i=ai(-t),b—i=bi(-t),c—i=ci(-t),i=0,1-9,t∈R.

下面研究當(dāng)系統(tǒng)(3)的反射函數(shù)為 F(t,x1,x2, x3) = (x1,x2,F3(t,x1,x2,x3))T時(shí),F3(t,x1,x2, x3)的具體表達(dá)式.

定理1 若 F1(t,x1,x2,x3)=x1,F2(t,x1,x2, x3)=x2,則 ai(0)=0,bi(0)=0,(i=0,1-9).

證明 若 F1(t,x1,x2,x3)=x1,F2(t,x1,x2, x3)=x2,則由反射函數(shù)的基本關(guān)系式(2)有,

由第一分量得,

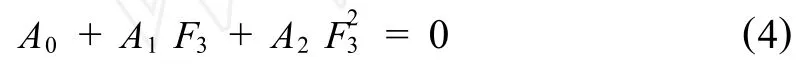
式中,A0=A0(t,x1,x2,x3)=P0+P1x3+P2x23+P—0,A1= A1(t,x1)=P—1,A2=A1(t,x1)=P—2,這里,P—i=Pi(-t, x),i=0,1,2.令t=0,則2[a0(0)+a1(0)x1(0)+a2(0) x2(0)+a3(0)x3(0)+a4(0)x21(0)+a5(0)x22(0)+a6(0)x23(0)+ a7(0)x1(0)x2(0)+a8(0)x1(0)x3(0)+a9(0)x2(0)x3(0)]=0.由 xi(0),i=1-3的任意性得,ai(0)=0,i=0,1 -9.同理,由第二分量可得,bi(0)=0,i=0,1-9.

下面總假設(shè),ai(0)=0,bi(0)=0,i=0,1-9.記號(hào),ai(t)≠0,bi(t)≠0(i=0,1-9),表示在 t =0的某去心領(lǐng)域內(nèi)成立.

定理2 若 F1(t,x1,x2,x3)=x1,a6=0,a23+ a28+a29≠0,或者 F2(t,x1,x2,x3)=x2,b6=0,b23+b28+b29≠0,則 F3(t,x1,x2,x3)=l0(t,x1,x2)+ l1(t,x1,x2)x3.

證明 若F1(t,x1,x2,x3)=x1,由式(4)得A0+ A1F3=0,而 a23+a28+a29≠0,故可推得定理的結(jié)論.若 F2(t,x1,x2,x3)=x2,b6=0,b23+b28+b29≠0,定理結(jié)論同理可得.

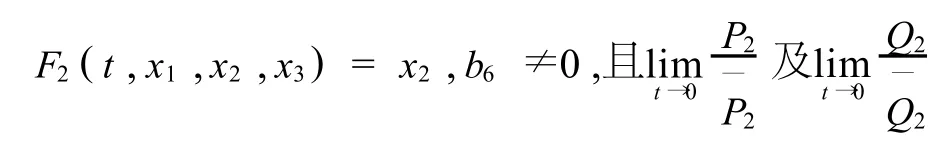
證明 若 F1(t,x1,x2,x3)=x1,由式(4)得,

再結(jié)合反射函數(shù)的性質(zhì),定理?xiàng)l件及 x3的任意性可得,

若 F2(t,x1,x2,x3)=x2,同理可得,

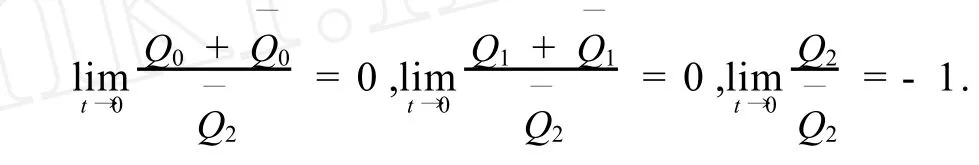
定理4 若a6≠0,b6≠0,系統(tǒng)(3)的反射函數(shù)為,

則必有,

證明 由反射函數(shù)的基本關(guān)系式得,

比較同類項(xiàng)的系數(shù)得,

由此可計(jì)算得,

再注意到,g0(0)=0,g1(0)=0,g2(0)=0, g3(0)=1,故有,

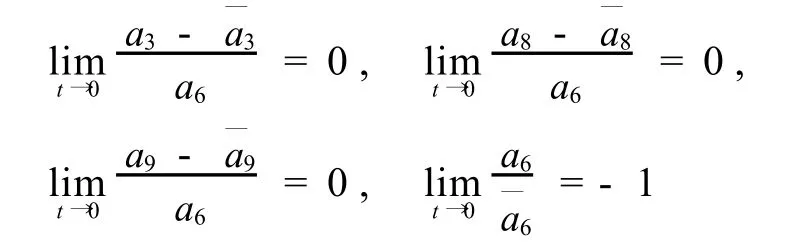
推論1 若a6=0,b6=0,a23+a28+a29≠0, b23+b28+a29≠0,系統(tǒng)(3)的反射函數(shù)為,則必有,

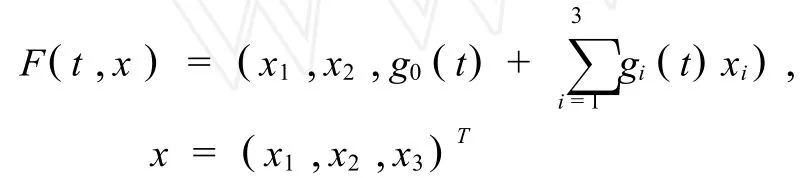
證明 與定理4同理可得.

定理5 若 a6≠0,b6≠0,系統(tǒng)(3)為2ω-周期系統(tǒng),且其反射函數(shù)為,

則當(dāng) gi(-ω)=0,(i=0-2),g3(-ω)=-1時(shí),系統(tǒng)(3)在[-ω,ω]上有定義的解均為2ω-周期解.

證明

則,

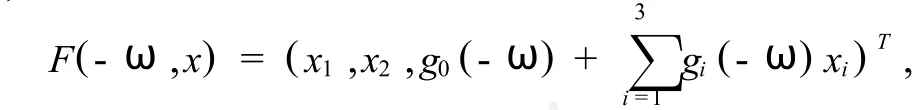
當(dāng)gi(-ω)=0,(i=0-2),g3(-ω)=-1時(shí),F(-ω,x)=x,故由引理1可得定理結(jié)論.

推論2 若a6=0,b6=0,a23+a28+a29≠0, b23+b28+b29≠0,系統(tǒng)(3)為2ω-周期系統(tǒng),且其反射函數(shù)為,

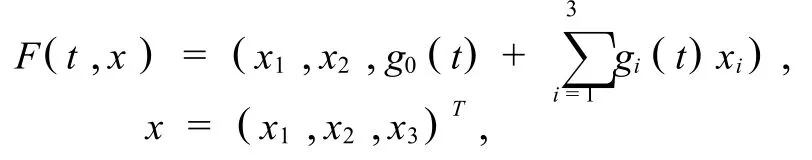
則當(dāng) gi(-ω)=0,(i=0-2),g3(-ω)=-1時(shí),系統(tǒng)(3)在[-ω,ω]上有定義的解均為2ω-周期解.

證明 與定理5同理可證.

[1]廖曉昕.穩(wěn)定性理論、方法和應(yīng)用[M].武漢:華中師范大學(xué)出版社,2001.

[2]許淞慶.常微分方程穩(wěn)定性理論[M].上海:上海科學(xué)出版社,1962.

[3]Arnold V I.Ordinary differential Equation[M].Moscow:Science Press,1971:198-240.

[4]Mironenko V I.Reflecting Function and Periodic Solution of the Differential System[M].Minsk:Minsk University Press,1986:12 -26.

[5]Mironenko V I.On the Method That Allows One to Determine the Initial Data of Periodic Solution of Differential Systems and to Compare the Mappings for a Period[J].Differ Eq,1980,14 (11):1985-1994.

[6]Alisevich L A.On Linear System With Triangular Reflective Function[J].Differ Eq,1983,19(8):1446-1449.

[7]Alisevich L A.On System with Diagonai Reflective Function[J]. Rrport of Belarus Science,1983,27(1):5-8.

[8]Veresovich P P.Non-autonomous Sectond Order Quadratic System Equivalent to Linear System[J].Ann Differ Eq,1998,14 (12):2257-2259.

[9]周正新.微分系統(tǒng)的反射函數(shù)與周期解[J].數(shù)學(xué)進(jìn)展, 2003,32(4):396-405.

[10]周正新.非線性微分系統(tǒng)的 Poincare′映射與周期解[J].系統(tǒng)科學(xué)與數(shù)學(xué),2006,26(1):59-68.

[11]Zhou Zhengxin.On the Poincare Mapping and Period Solutions of Nonautonomous Differential Systems[J].Commuuications on Pure and Applied Analysis,2007,60(2):541-547.

[12]章山林,周正新.多項(xiàng)式微分系統(tǒng)的周期解[J].數(shù)學(xué)的實(shí)踐與認(rèn)識(shí),2009,39(17):159-164.