中間λ康托集上可積函數空間的可分性

胡曉梅

(咸寧學院數學與統計學院,湖北咸寧 437100)

中間λ康托集上可積函數空間的可分性

胡曉梅

(咸寧學院數學與統計學院,湖北咸寧 437100)

通過一類特殊的分形集——中間λ康托集的構造,得到它的一些重要拓撲性質和分形特征,進而利用Stone-Weierstrass定理,證明了中間λ康托集上 P方可積函數空間是可分的。

中間λ康托集;可積函數空間;可分性

1 預備知識

定義1(IFS) 設(Rn,d)為n維歐氏空間,如果對任意i∈{1,2,…,N},fi:Rn→Rn是壓縮映射,即對任意 x,y∈Rn,存在 r1∈(0,1),使得d(fi(x),fi(y))≤rid(x,y),則稱壓縮映射族{fi}為(Rn,d)上一個迭代函數系統。如果上式取等號,則稱 fi為相似壓縮映射。

Hutchinson已證明對于給定的 IFS{fi},必存在唯一非空緊集 K?Rn滿足稱 K為關于迭代函數系統{fi}的不變集或吸引子[2]。例如由相似壓縮迭代函數系統生成的不變集 C就是通常意義下的三分Cantor集。它是一個自相似集[3]。

定義2設一非負集函數μ:{A:A?X}→[0,∞]滿足

1)μ(φ)=0;

對于給定的IFS{f1,f2…,fN}和滿足pi＞0,1≤i≤N的概率向量 P=(p1,p2,…,pN),Hutchinson在文獻[2]中已證明存在唯一的μ∈U,使得對任意的Borel集 A,有μ(A)=稱滿足上式的測度為關于IFS和P的不變測度。

特別地,當上述IFS是一族相似壓縮映射時,此測度就稱為關于它們的自相似測度。

定義 3設 f(x)是 F上的可測函數,記其中 F為中間λ康托集,μ為關于IFS和P=(1/2,1/2)的自相似測度。用 Lp(F,μ)表示‖f‖p＜ ∞的函數 f的全體組成的函數空間。

顯然Lp(F,μ)是線性賦范空間,‖.‖p為其范數。

定義4設г是Lp(F,μ)中的子集,若對任意的 f∈Lp(F,μ)以及ε＞0,存在 g∈г使得 ‖f-g ‖ ＜ε,則稱 г在Lp(F,μ)中稠密。若 Lp(F,μ)中存在可數稠密子集,則稱Lp(F,μ)是可分的。

2 中間λ康托集F的構造及性質

考慮閉區間 E0=[0,1]。

將 E0=[0,1]正中間去掉一個長度為原區間長度的λ(0＜λ＜1)倍的開區間剩下兩個閉區間記E1為它們的并;再把E1中的這兩個閉區間正中間分別去掉長度為它們各自區間長度的λ倍的開區間,得到集合 E2;然后將 E2中余下的四個閉區間同法處理得到集合 E3,如此繼續下去,每一步都去掉區間中間一段比例為λ的部分,在第k步我們得到2k個長度為的閉區間,其并記為 Ek,當k→∞時,序列 Ek的極限集就是我們所構造出的中間λ康托集 F。顯然,三分Cantor集為 F在λ時的特例。

由上面中間λ康托集F的構造容易得到F具有如下幾條重要的性質:

1)是非空有界閉集;

2)是完全集;

3)無內點,即是無處稠密集;

4)完全不連通;

3 Lp(F,μ)的可分性及證明

引理1[4](控制收斂定理) 設{fn}是可測集 X上的可測函數列,μ是X上的測度。如果存在非負函數 g(x)∈(X,μ)滿足

2)對所有的x∈X和任意的n,有 ︱fn(x)︱≤g(x),則 f ∈L(X,μ),且

命題1設1≤p≤∞,則任給 f∈Lp(F,μ),均存在Lp(F,μ)中的簡單函數列使得當n→∞時,Sn幾乎處處收斂到f,并且 ‖fsn‖p→0和

引理2[4](Lusin’s定理) 設 f(x)是可測集X上的可測函數,μ為 X上的測度。令 A={x∈X︱f(x)≠0},如果μ(A)＜ ∞,則任給ε＞0,均有G∈Cc(X)使得μ({x∈X︱f(x)≠g(x)})＜ε,并且經過適當選取有

引理3[5](Stone-Weierstrass定理) 設 Ω是Rd中的一個緊子集,令表示全體實系數d個變量的多項式全體,則在 C(Ω,R)中稠密,即對任意 f∈C(Ω,R)均存在d個變量的實系數多項式無限的逼近。

由于 C(F,R)滿足該定理的條件,從而 F上實系數多項式在C(F,R)中稠密。另外因為任給一個實數均可以由有理數來逼近,即每一個實系數多項式均存在一有理系數的多項式來逼近,這即說明了 F上有理系數多項式全體在C(F,R)中稠密。

定理C(F,R)在 Lp(F,μ)中稠密,且Lp(F,μ)為可分空間(1≤p≤∞)。

證明令S表示 F上所有可測簡單函數全體,因為μ(F)=1,從而μ({x︱s(x)≠0})＜ ∞。我們首先證明 S在Lp(F,μ)中稠密。顯然 S?Lp(F,μ),我們先設 f＞ 0,由命題1知存在 F上的可測簡單函數列{sn}幾乎處處收斂于 f,并且0≤sn≤f。從而sn∈Lp(F,μ),這也即說明了sn∈S。又 ︱f-sn︱p,則由引理1的控制收斂定理,當n→∞時,‖f-sn‖p→0。對于一般的 f,因為f(x)=f+(x)-f-(x),這里

因此我們分別再對 f+(x)和 f-(x)作上面相同的論證 ,即存在和按照范數 ‖. ‖p分別收斂到 f+(x)和 f-(x)。令

綜上,S在Lp(F,μ)中稠密。再來證 C(F,R)在Lp(F,μ)中稠密。設s∈S,對于任給的ε＞0,由引理2的Lusin’s定理知,存在 g∈C(F,R)使得μ({g(x)≠s(x)}),并且適當選擇有。因此,

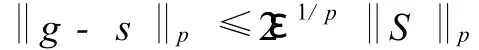
又由Minkowski’s不等式得

這即說明了 C(F,R)在 中稠密。最后證Lp(F,μ)為可分空間。由引理3知 F上有理系數多項式全體在C(F,R)中稠密,而 C(F,R)在 Lp(F,μ)中稠密,故 F上有理系數多項式全體在Lp(F,μ)中稠密,而所有有理數全體是可數集,從而空間Lp(F,μ) 可分。

[1] 胡曉梅.三分Cantor集上 p方可積函數空間Lp(C,μ)的可分性.佳木斯大學學報,2008,26(6).

[2] Hutchinson J E.Fractal and Self-similarity[J].Indiana Univ M ath,1981,30(5):713-747.

[3] Falconer K J.Fractal Geometry:Mathematical Foundation and App lications[M].New York:John Wiley and Sons,1990.

[4] Rudin W.實分析與復分析[M].北京:機械工業出版社,2004.

[5] M cdonald J N,Weiss N A.A Course in Real Analysis[M].北京:世界圖書出版公司,2005.

Separability of the Space of Integrable Function on the MiddleλCan tor Set

Hu Xiaomei
(School of Mathematics and Statistics,Xianning University,Xianning,Hubei 437100,China)

By analyzing the construction of the middleλCantor set,a typical fractal set,this paper discussed some topological properties and fractal characters of the middleλCantor set firstly,and then p roved that the space of integrable function Lp(F,μ)(1≤p≤∞)is separable by using the Stone-Weierstrass theorem.

the middleλCantor set;space of integrable function;separability

O177

A

1671-2544(2010)03-0026-03

2009-11-02

咸寧學院科研項目(ky09060)

胡曉梅(1979— ),女,湖北咸寧人,咸寧學院數學與統計學院講師,碩士。

(責任編輯:周 游)