無底柱分段崩落法放出體、松動體、崩落體三者關系模型

張國建，翟會超

(1.遼寧科技大學，遼寧 鞍山 114051；2.東北大學, 遼寧 沈陽 110004)

無底柱分段崩落法是在覆蓋巖層下進行放礦和落礦的，損失貧化大是該采礦方法的主要問題之一，為改善該法的開采效果，國內外專家學者及礦山工作人員做了大量研究工作，也取得了很大的成績，但仍沒有達到人們滿意的結果。

分析其原因主要是：在過去無底柱分段崩落法的研究中，有的側重放礦，有的側重爆破，沒有把回采過程作為有機整體來研究，缺乏對回采過程中放出體、松動體、崩落體三者關系的研究。回采過程中的放礦與爆破落礦是緊密相連、相互制約的，研究放出體、松動體、崩落體三者之間的內在規律，建立三者的關系模型，對降低礦石損失貧化，提高礦山經濟效益有重要意義。

1 放出體、松動體、崩落體三者關系模型

在井下落礦、放礦的循環過程中，崩落體影響放出體的形成，放出體又影響松動體的形成，松動體又會影響下一次落礦中崩落體的形成和發育。因此，放出體、松動體、崩落體在回采過程中是依次相互制約的，見圖1。

圖1 三者關系圖

以放出體為每次循環起點，從體積量參數出發，放出體、松動體和崩落體三者體積有如下函數關系：

Vf1=f(Vb1)，Vs1=f(Vf1)；

Vb2=f(Vs1),Vf2=f(Vb2)；Vs2=f(Vf2)；

Vf3=f(Vb2)，Vs3=f(Vf3)，Vb3=f(Vs3)；

……

……

Vfn=f(Vbn-1)，Vsn=f(Vfn)，Vbn=f(Vsn)。

式中：Vs—松動體體積Vf—放出體體積；Vs—崩落體體積；n—循環次數。

根據礦山現場的實際情況，可以應用一定的方法來確定上述函數的具體形式，從而建立符合礦山實際的放出體、松動體、崩落體體積關系模型，來預測和控制回采過程落礦與放礦。

2 體積關系模型確立方法

在實際生產過程中，可以運用已有數據求解未知參數，從而建立放出體、松動體、崩落體三者體積關系模型。

2.1 放出散體與放出體體積比值

崩落體是指在爆破作用下，在松散圍巖中形成的爆堆，是放礦的對象，崩落體的密度也就是放出體的密度。爆破作用前后，礦石的質量不變，密度變小、體積變大，發生第一次松散，松散系數為Ks1。

由質量守恒定律可得：

∵m礦體=mb

∴ρ礦體V礦體=ρbVb

第一次松散系數Ks1可表示為：

式中：m礦體、mb—爆破前后礦石質量；ρ礦體、V礦體—爆破前被爆礦體的密度和體積；ρb、Vb—爆破后崩落體的密度和體積。

生產過程中，鏟運機鏟斗中的礦石散體被動稱為“放出散體”，其松散狀態近似于無約束條件的自然堆積，而放出散體與放出體的質量完全相等，只是在礦石放出后，其體積、密度發生變化，分為放出體體積和放出散體體積(如圖2)。

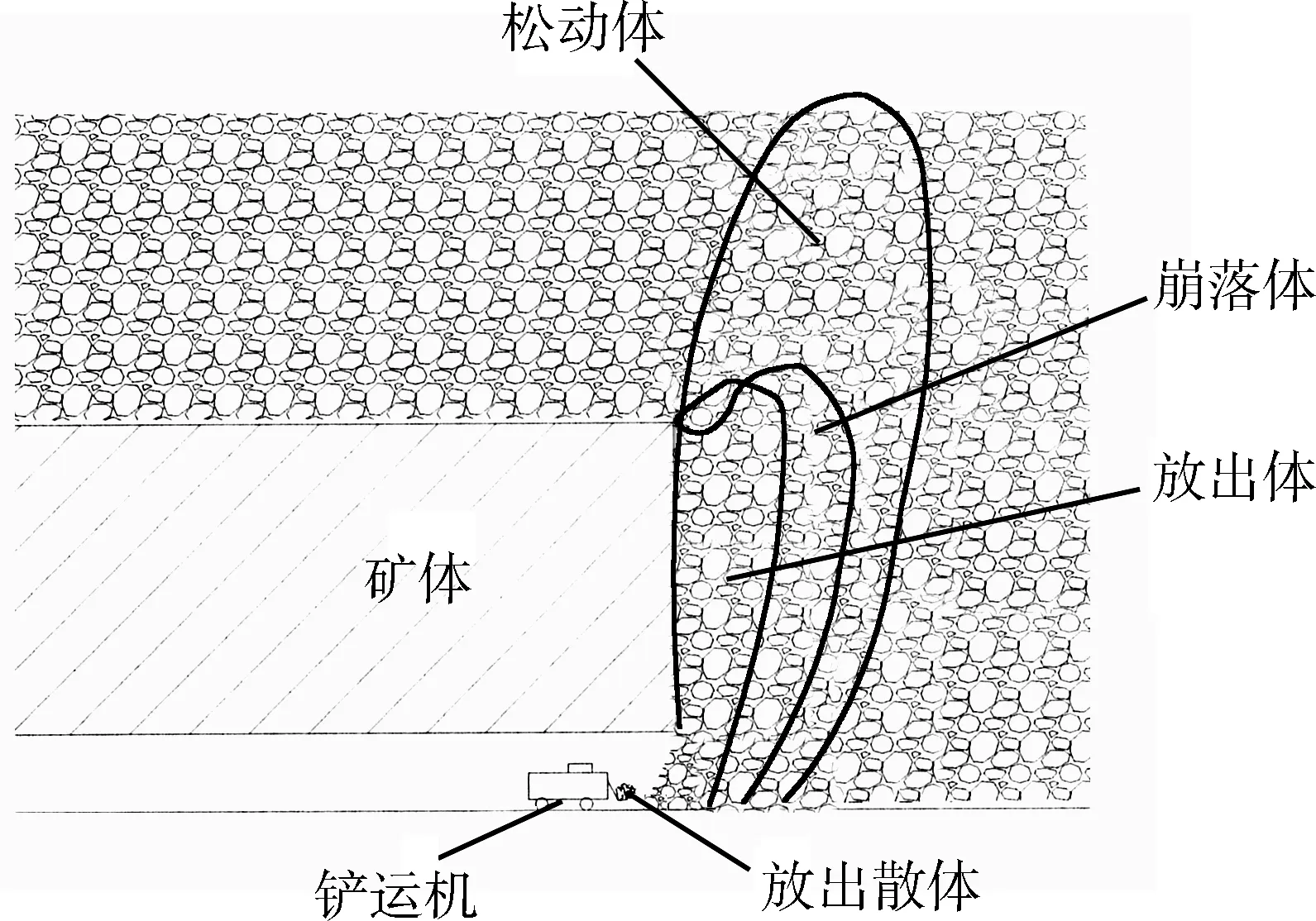
圖2 礦石開采示意圖

同樣由質量守恒定律：

∵mf=mfs

∴ρfVf=ρfsVfs

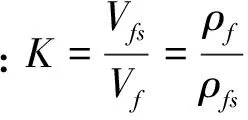
式中：mf、mfs—放出體和放出散體的質量；ρf、ρfs、Vf、Vfs—放出體和放出散體狀態下的密度與體積。

注：ρfs即為鏟斗內礦石密度，所以放出體的密度可求解：ρf=ρfs*K

可見放出散體與放出體體積的比值K是確定放出體、崩落體相關參數以及崩落體體積的依據。

2.2 單一循環三者體積量的確定

無底柱分段崩落法回采進路的一次落礦、放礦循環中，放出體、松動體、崩落體三者的體積量可以按照一定的方法求得。

首先，放出散體體積。放出散體相關參數可由井下出礦設備鏟運機的斗容、出礦差斗數和平均斗內散體密度來求解，這些都是已知的。即通過進路一次崩落礦石生后所放出礦石的總量，就可以得到放出散體(礦石)的體積。

其次，放出體、松動體體積。根據放礦理論得知，放出散體體積與放出體體積存在一定的聯系：

在進路尺寸、進路間距、進路布置形式以及分段高度等參數確定后，就可以根據放出散體體積和上述公式間接地求出放出體的體積。于是，松動體體積可求：

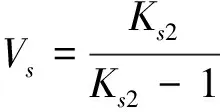
最后，崩落體體積。有了放出散體和放出體的體積量，可知二者的體積比值K。再根據質量守恒定律，便可得到放出散體在覆巖中，即放出體形態內的密度(參見上文)，該密度就是崩落體的密度。而崩落體在原礦體形態中，即落礦前礦體的密度是已知的。這樣，崩落后的礦石堆體(崩落體)密度ρb與原礦體的密度ρ礦體之比就是一次松散系數Ks1.根據落礦前爆破設計的礦體崩落范圍，可獲得礦石崩落前的體積，再與一次松散系數聯合得出崩落體體積。

Vb=Ks1×V礦體

以上單一循環中三者體積的求解過程見圖3。

圖3 單循環三者體積求解流程度圖

2.3 三者體積關系的確定

通過上述方法可以求解每次落礦、放礦過程度中的放出體、松動體、崩落休體積量。這樣，依據礦山的大量生產數據，可得到放出體、松動體、崩落休體積量。并根據三者的相互制約關系，對其兩兩關系進行聯立，通過數值分析進行離散數據的回歸，得出放出體和松動體、松動體和崩落體、崩落體和放出體(可解放出體)的體積關系數學模型，再按照落礦、放礦作業的銜接關系建立循環體積關系模型。這樣，便可得到該礦山販放出體、松動體、崩落體三者體積關系模型。建立循環體積關系應用這種方法，課題組對弓長嶺井下鐵礦的歷史數據進行初步分析，得到了較為符合弓長嶺鐵礦的放出體、松動體、崩落休三者體積關系的具體數學模型，并運用該模型對礦山生產進行指導，打破截止品位放礦的界限，控制出礦量或崩落礦石量，為下次落礦崩落體形態發育創造良好環境，提高崩落體的放出性，從而使得井下礦石回收率得到提高。

3 結 論

本文闡述了無底柱分段崩落法中放出體、松動體、崩落體三者之間的內在聯系，從體積參數角度建立放出體、松動體和崩落體之間的一般循環函數關系。并敘述、推導了函數具體形式的解法。其中，分析了放出散體體積與放出體體積的比值對求解函數的重要作用，并應用放礦學理論可分別得到崩落體與放出散體、放出散體與放出體、放出體與松動體、松動體與崩落體的體積函數式，從而建立起放出體、松動體、崩落體三者的體積循環模型。該方法在弓長嶺井下鐵礦進行了初步應用，并取得一定的效果。

[1] 王昌漢.放礦學.北京：冶金工業出版社，1982.

[2] 張國建，郭連軍.無底柱分段崩落礦石形態及其影響研究.中國礦業，1997，6(3)：27-31.

[3] 張國建. 無底柱分段崩落法應進一步研究的幾個問題 .中國礦業，2003，12(11)：41-43.

[4] 張國建，蔡美峰.崩落體形態及其影響研究 .中國礦業，2003，12(12)：38-42.