大斷面軟巖巷道支護加固技術研究

薛道成

(山西焦煤西山煤電集團公司，山西 太原 030053)

1 概 述

由于煤炭賦存條件的復雜、多變，煤炭開采條件的不可選擇性，多數礦井的生產和建設都將面臨不同程度、不同數量的軟巖巷道開掘及維護難題。特別是服務年限較長的準備巷道、開拓巷道施工、維護，需解決一系列軟巖巷道問題，比如巷道自穩時間短、變形大、難維護、返修率高等。加之多數軟巖巷道斷面較大，巷道變形破壞的影響因素復雜[1]，在支護設計中，要考慮多方面影響因素的嚴重程度、作用機理。根據軟巖特性，采用主動組合支護手段，使施工工藝在空間、時間、圍巖特性三方協調，變形在控的新型耦合支護技術，即三維協控支護技術。本文結合古交礦區復合頂板煤礦軟巖巷道支護實際，通過圍巖物理力學特性研究、現場地質資料分析、礦壓顯現規律的定性和定量研究，借助數值分析、相似模擬等手段，提出三維協控支護技術方案，并進行現場試驗，取得了預期效果。

2 巷道地質條件

2.1 巷道斷面特性

本文研究軟巖大斷面巷道以馬蘭礦南部軌道下山為實驗對象，巷道斷面形狀為半圓拱形，凈寬4.2m，凈高3.5m，凈斷面積12.8m2，其間車場巷道凈斷面積15.7m2，巷道頂底板、兩幫移近量局部高達1.0m，平均移近量大于600mm，且巷道處于長期流變、蠕變狀態，巷道斷面不能滿足生產需要，需頻繁返修，嚴重影響正常生產，造成采掘接替緊張。

2.2 巷道層位及構造

巷道施工過程中，主要揭露巖性為：泥巖，厚度較大(平均>5.0m)，灰色、塊狀、含植物化石碎片，局部較破碎；粉砂巖(平均>2.5m)、鋁質泥巖(平均>7.5m)，局部穿過中、細砂巖(平均<2.0m)，淺灰色、薄層狀、堅硬，含石英及暗色礦物，水平狀層理。

巷道構造情況：該處煤巖層產狀變化較大，施工范圍內基本為北北東向，傾角50～160。

3 巷道圍巖特性

3.1 微觀礦物組成

南部軌道下山頂板巖石所含礦物，包括非黏土礦物石英、方解石、黃鐵礦、菱鐵礦、角閃石，黏土礦物伊利石、高嶺石、伊蒙混層，巖石表現為易風化、易膨脹、易脆性碎粒破壞特性，抵抗風、水及其他化學環境侵蝕的能力較差，對巖石的整體長期穩定不利。

3.2 微觀結構

南部軌道下山巖石整體屬層狀構造，連通性較好、微裂隙發育、聯結強度較弱，對整體結構及強度影響較大。粒間、層間空隙發育，空隙由黏土礦物及部分黑色機質充填，容易產生局部層間錯動或碎粒狀破壞。層理結構明顯，強度低、硬度小、結構完整性較差，對環境的適應性不強。在施工及支護中，應注意控制變形及圍巖的封閉，并在合理設計支護強度的條件下，保持連續可控變形。

4 支護方案設計

4.1 錨桿參數計算

4.1.1 錨桿長度

通常錨桿長度等于外露長度l1、有效長度l2與錨固段長度l3之和。即

l=l1+l2+l3

式中：l為錨桿總長度，m；l1為錨桿外露長度，不大于0.15m；l2為錨桿有效長度，m；l3為錨桿錨固長度，取0.3～0.4m。

結合本巷道支護結構，l2按組合梁(拱)理論計算較合理，計算公式如下：

式中：q為組合梁上的均布荷載，MPa；σx為原巖水平應力，σx=λγ·Z，MPa；σt為巖石抗拉強度，MPa；ξ為組合巖層數目的系數，0.75；k1為抗拉安全系數，取2～3；λ為側壓力系數，0.5；L為巷道跨度。

將巷道數據代入公式計算得：

l2=0.193×4.2

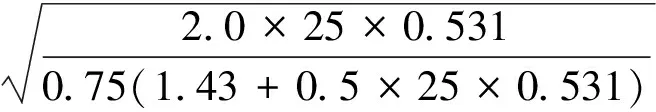
代入公式，l=l1+l2+l3=0.15+1.69+(0.3～0.4)=2.14～2.24m

幫部錨桿長度：考慮錨桿支護材料配套及幫頂松動破壞范圍的關系，幫部錨桿長度對應為2.2m或2.4m，為材料的統一配置，頂幫錨桿長度都取2.4m。

4.1.2 錨桿的錨固力

錨桿的錨固力P(kN)取決于巖石硬度，按下式計算：

式中：d為錨桿直徑，m；f為錨固段巖層的硬度系數；σt為錨桿桿體的極限抗拉強度，MPa。直徑為φ20mm的錨桿的抗拉強度能達到500MPa。

帶入數據，得頂錨桿的錨固力P頂=85.7 kN；幫錨桿的錨固力為P榜=85.7kN。

4.1.3 錨桿的間距、排距計算

通常間、排距相等，取為a。并根據錨桿的錨固力應大于被懸吊巖石的重量的原則確定，即：

式中：a為錨桿的間、排距，m；K為無因次安全系數，3～5；Q為錨桿的設計錨固力，85kN；γ為被懸吊巖石的重力密度，取25kN/m3。

考慮炮掘施工安全系數，實際a取0.7m，可滿足生產需求。

4.2 錨索參數計算

4.2.1 錨固長度

在錨索支護設計中，應保證鋼絞線與膠結體有足夠的黏結強度，才能保證錨索的支護效果。大量工程實踐表明：樹脂藥包錨索錨固長度應≥1.0m。使用1支K2370、2支Z2370樹脂錨固劑的實際錨固長度為：

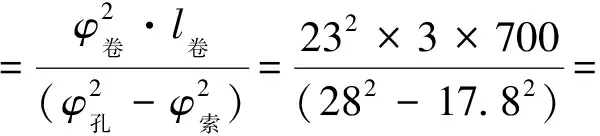
2377.98mm>La

能滿足錨索生根穩固巖層的要求。

4.2.2 錨索長度

錨索宜錨固在圍巖內部較穩定的巖層中。錨索長度按下式計算：

L=La+Lb+Lc+Ld

式中：L為錨索的總長度，m；La為錨索深入到較穩定巖層的錨固長度，取1.1m；Lb為需要懸吊的不穩定巖層厚度，根據南部軌道下山煤巖綜合柱狀圖，取8.0m；Lc為上托板及錨具的厚度(一般≥0.1m)，取0.15m；Ld為需要外露的張拉長度(一般≥0.2m)，取0.25m。

考慮直接頂厚度的不均勻性和施工影響因素，安全系數取1.05～1.1，則南部軌道下山錨索的長度為：LS=9.975～10.45m。

故，錨索長度選取10.5m為宜。

4.2.3 錨索支護密度

式中：N為錨索數目；P1為錨索的最低破斷力；W為每平方米巷道的靜壓力，W=∑h·∑γ； ∑h為懸吊的巖層厚度； ∑γ為懸吊的巖層的平均容重。

潛在的冒落高度一般為1.5倍的巷道寬度，計算得6.3m。

錨索的最低破斷載荷P1為353kN，考慮到錨桿支護體系的應有作用，安全系數K取1.1，則N=1.1×6.3×25/353=0.49根/m2，該數值為錨索支護應有的支護密度。

錨桿排距為700mm時，當錨索排距3×700=2100mm，則每排需要的錨索數量n=2.1×4.2×0.49=4.32根，考慮后續注漿加固發揮圍巖自承能力，取3根。

4.3 數值分析

本文應用FLAC3D對巷道底角錨桿的位置及下扎角度進行數值模擬分析，通過調整其距底板的距離及下扎角度(與底板水平面夾角)兩個參數，對比分析巷道塑性變形破壞范圍、頂底板移近量、兩幫移近量，確定距底板的距離200mm、下扎角度150時，支護效果最佳。由于篇幅所限，模擬過程及圖表略。

故在方案設計中，巷道底角錨桿布置如圖1所示。

4.4 支護方案

主要對策為組合式支護措施，主要支護環節為：圍巖注漿以提高圍巖整體性和強度；利用錨索調動深部圍巖強度；加固兩幫控制內移；全斷面后路注漿提高圍巖整體穩定性及自承能力，采用底角注漿錨桿控制巷道底板穩定性[2-5]。

(1)錨桿規格及其布置。使用φ20左旋螺紋鋼高強度(粗尾)錨桿，長度為2400 mm，巷道兩底角錨桿與水平面夾角為15°，其余錨桿均垂直巷道表面布置(圖1)。

(2)錨固方式。采用K/Z2370速凝樹脂藥卷，每個鉆孔需1根藥卷。

(3)頂板鋪設鋼筋網、兩幫加鋼筋梯。

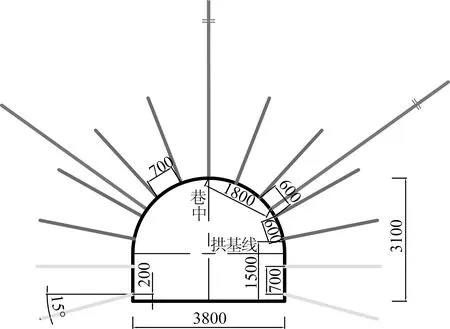
圖1 南部軌道下山錨桿(索)支護方案

(4)錨索。采用預應力錨索，長度取10.5 m，結合施工實際實時調整具體長度。初步確定錨索間距布置如圖1所示。使用3支K/Z2370的樹脂藥卷加長錨固。

(5)圍巖注漿補強加固。注漿錨桿將錨固和注漿結合在一起，提高巖體強度，形成承載結構、改善賦存環境[3]。注漿錨桿長2.4 m，間距(1.6m)、排距為1.4m(擴散半徑0.8～1.0m)，除下底角注漿孔(與水平方向偏下夾角30°)外，其余孔均垂直巷道巖面布置，注漿孔布置見圖2。

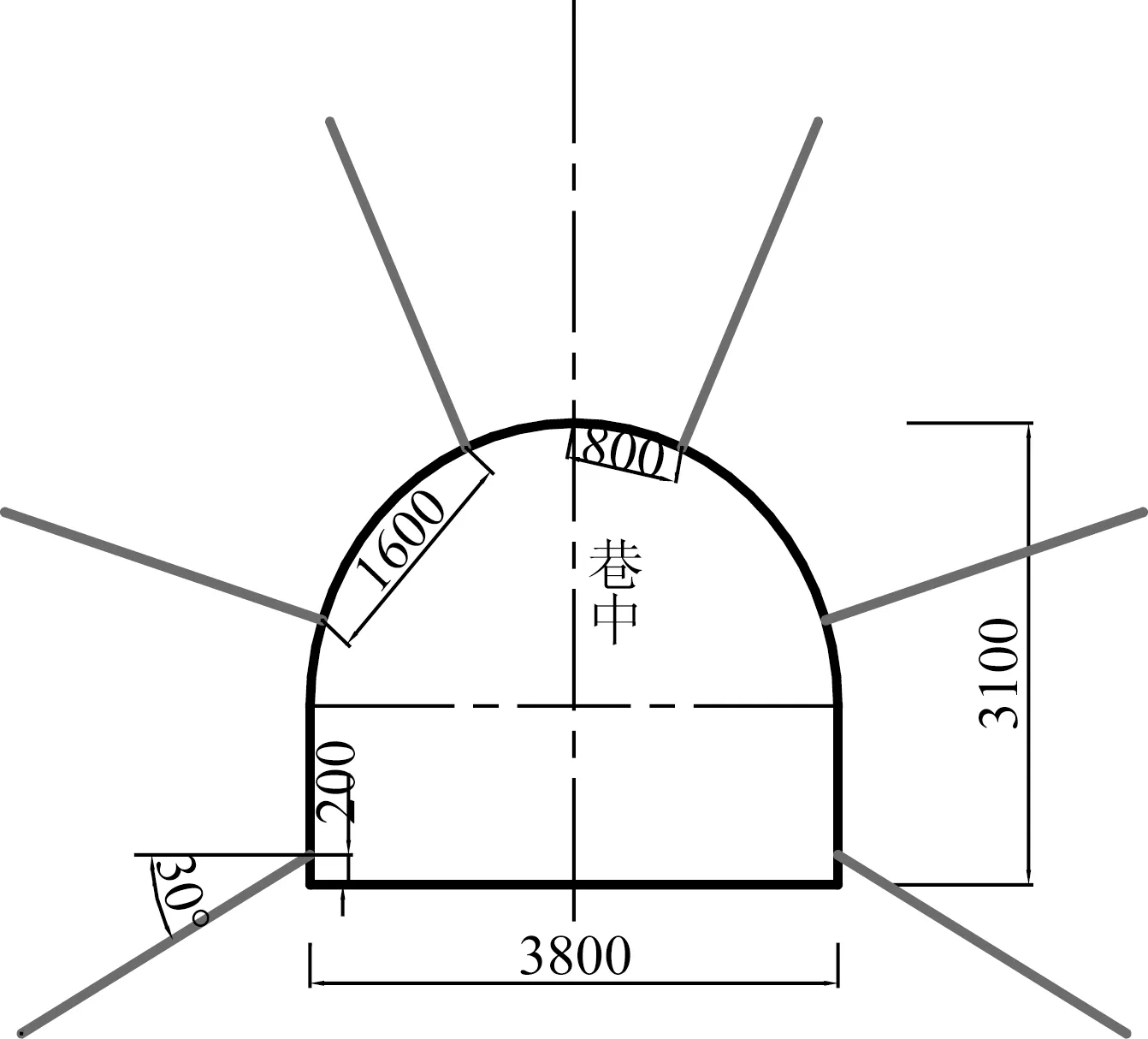
圖2 注漿技術方案

4.4 支護效果分析

4.4.1 變形量

巷道位移及收斂速率是反映巷道圍巖變形和穩定性狀態的重要指標。課題組于2009年7月21日～2009年8月29日和2009年9月5日～2009年10月15日兩個時段，在現場進行了巷道圍巖變形觀測。

圖3和圖4分別是巷道掘出后，第I測站和第Ⅱ測站巷道圍巖表面位移量、位移速度隨時間的變化情況。可看出，南部軌道下山掘進期間兩幫和頂底收斂位移隨時間的變化特征。

掘進期間巷道變形觀測結果見表1、表2。

4.4.2 變形速度

掘進影響期巷道表面位移量較大，14d掘進進尺29.4m，巷道兩幫位移為99mm，兩幫位移速度最大為6.0～6.1mm /d，頂板位移量47mm，底臌量為113mm，頂底位移速度最大為5.3～9.2mm /d。

進入穩定期后，巷道表面位移量增速大大降低，兩幫位移速度在0.3～0.7mm /d左右。

表1 掘進期間巷道表面變形情況一覽表

表2 南部軌道下山表面位移觀測統計整理表

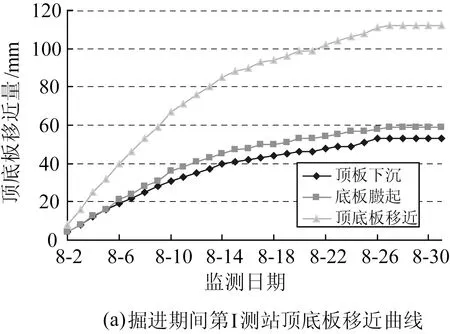
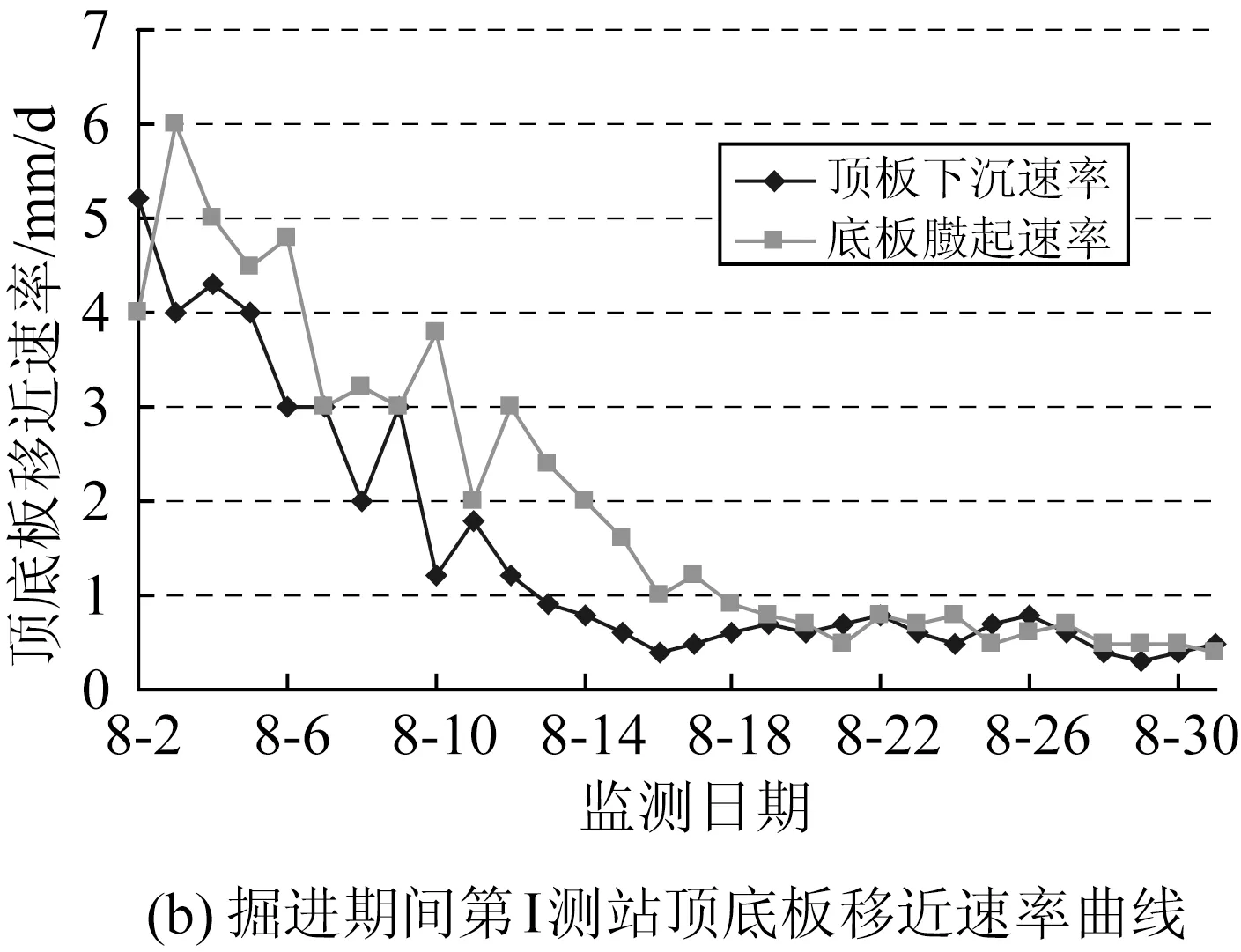
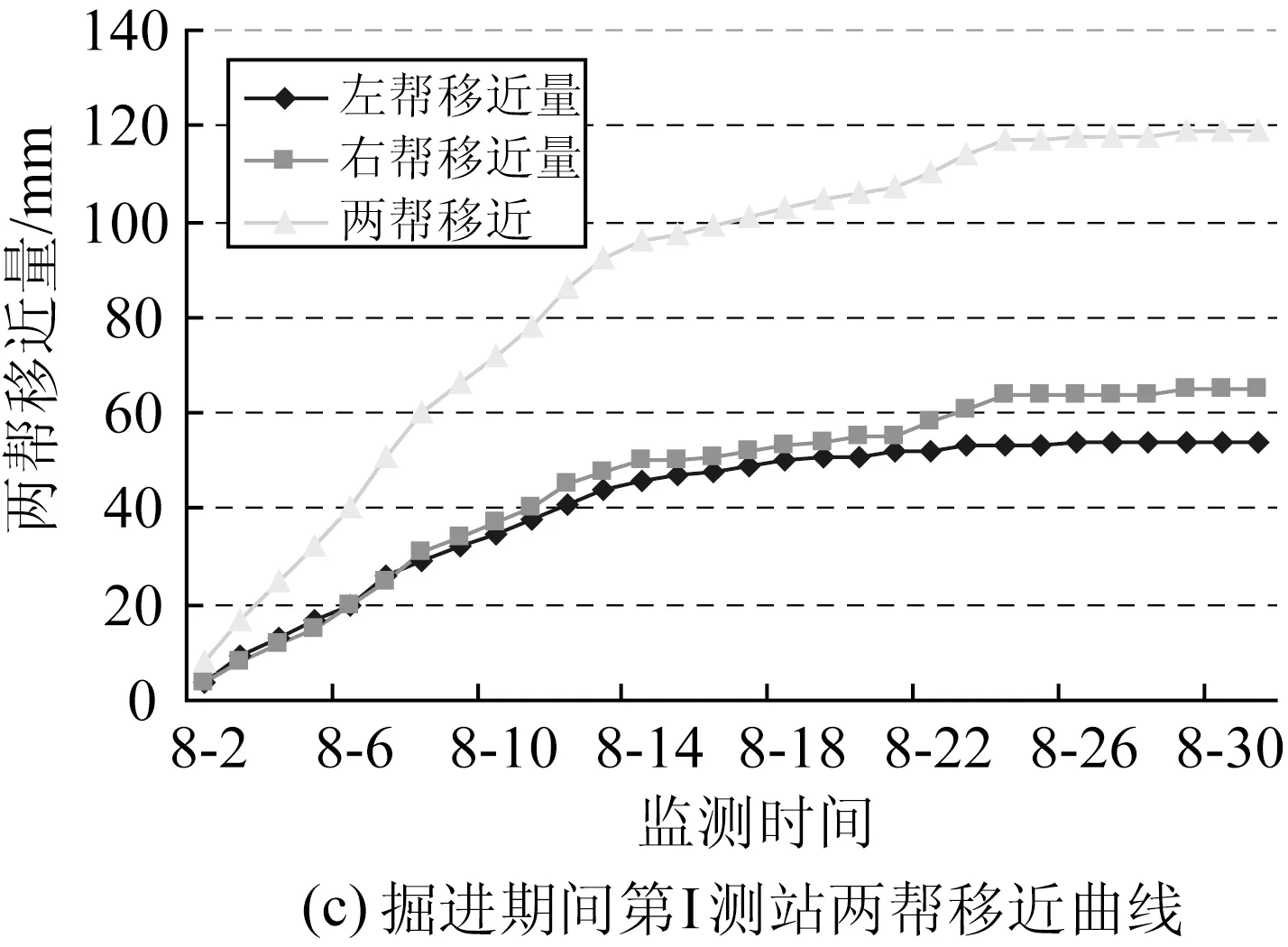
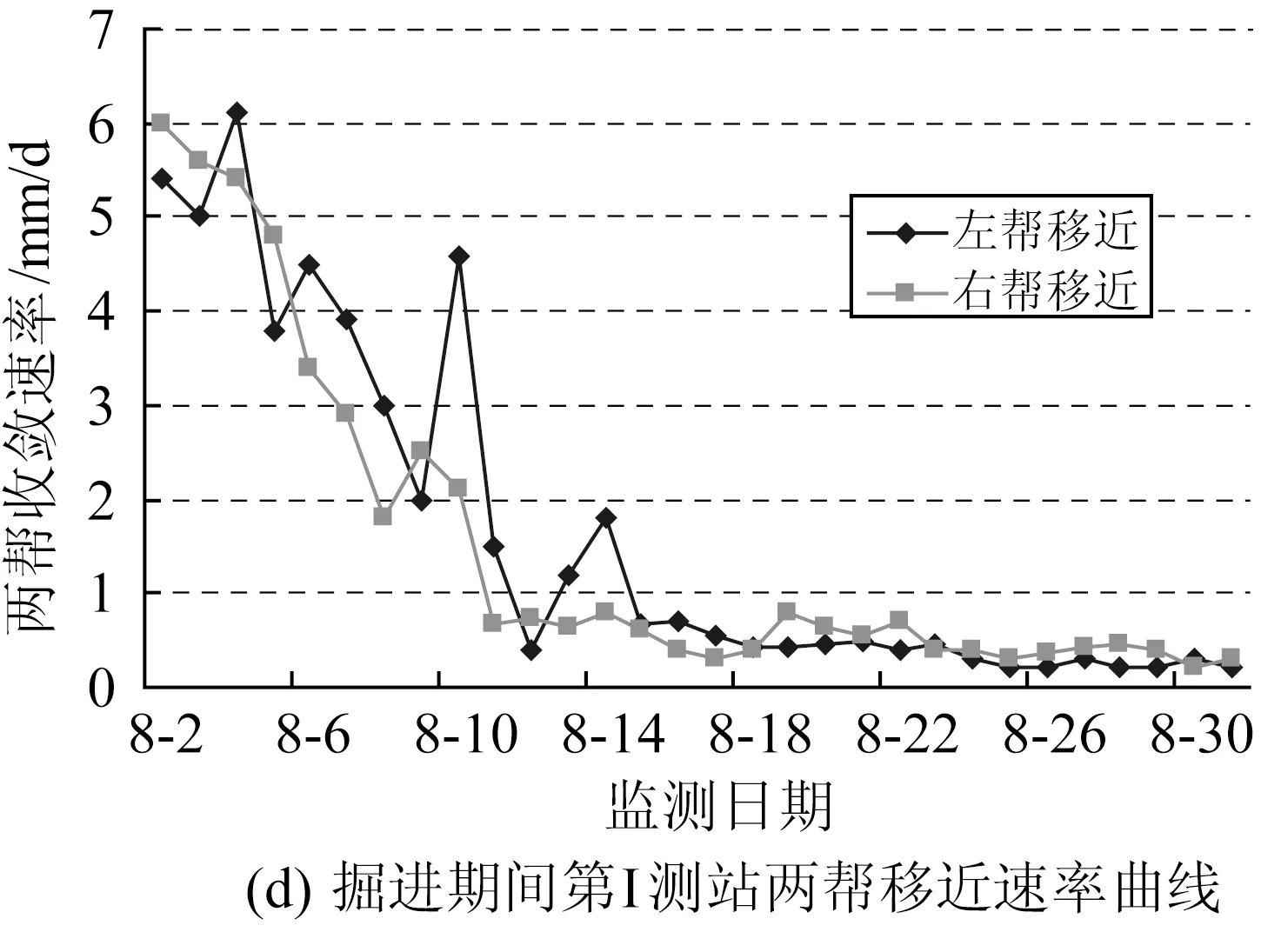
圖3 掘進期間第I測站圍巖收斂曲線

5 結 論

(1)軟巖巷道支護設計，必須掌握軟巖類型及變形破壞機理，需特別注意對巷道底板的加固，將巷道頂、幫、底視為巷道系統的統一體，三方實現穩定互補互助。

(2)為了充分發揮噴漿對巷道環境適應性及整體穩定性的提高作用，以便發揮圍巖潛在的自承能力，須結合巷道變形實際，合理確定噴漿厚度、初噴和復噴時間間隔及其他噴漿參數。

(3)支護設計需結合巷道圍巖變形破壞特征，采用三維協控技術。在方案設計中，采用的支護材料須幾何尺寸、特性協調配合，施工工藝在時間和空間上與圍巖變形耦合，保證巷道變形在控。

(4)通過現場試驗，認為本文所采用的支護技術對類似巷道支護有效，具有實際應用價值。

(5)錨注補強加固對軟弱圍巖巷道具有很好效果，但須注意注漿材料選擇，注漿時間、注漿壓力、注漿量等參數的合理協調和優化。

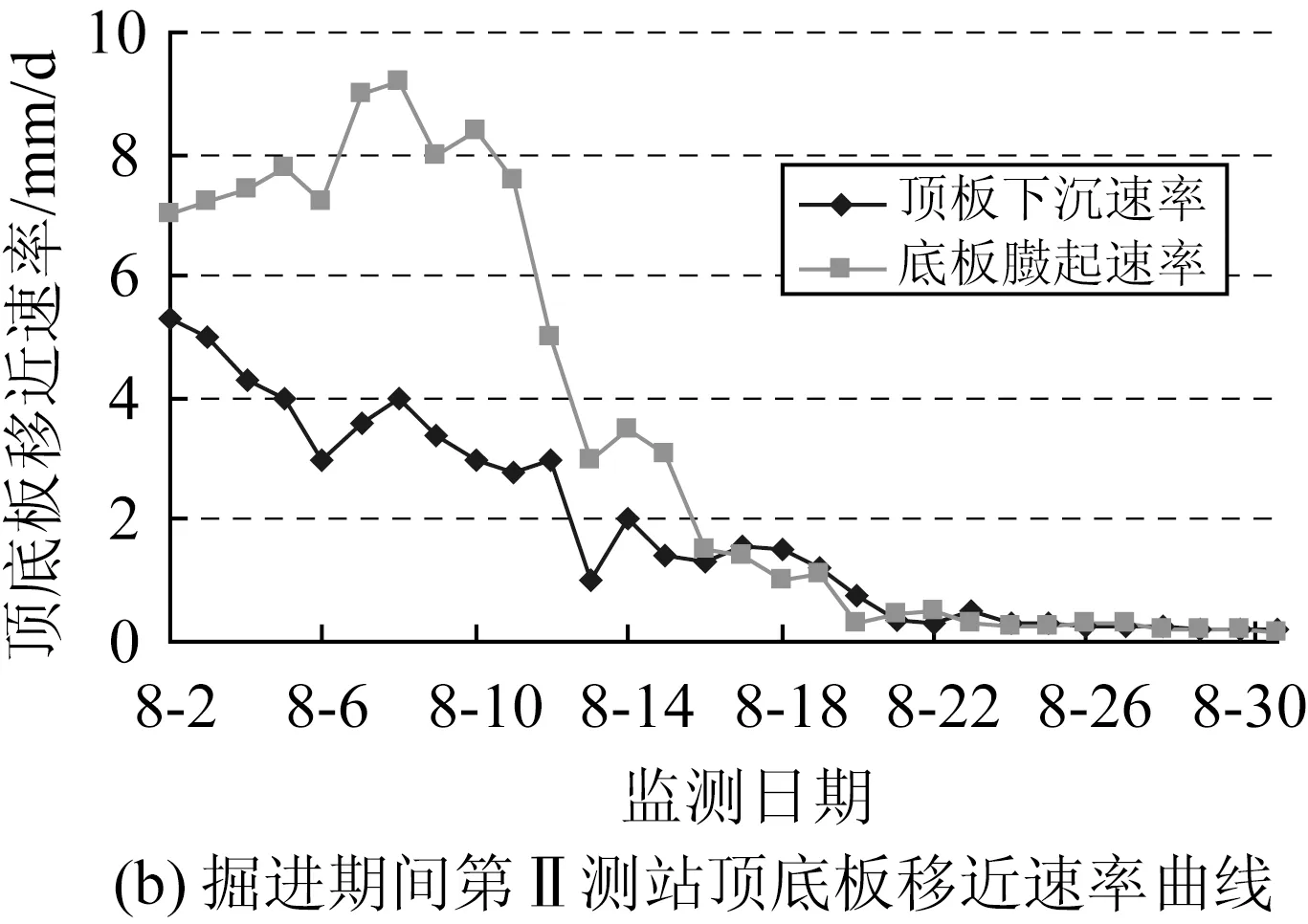
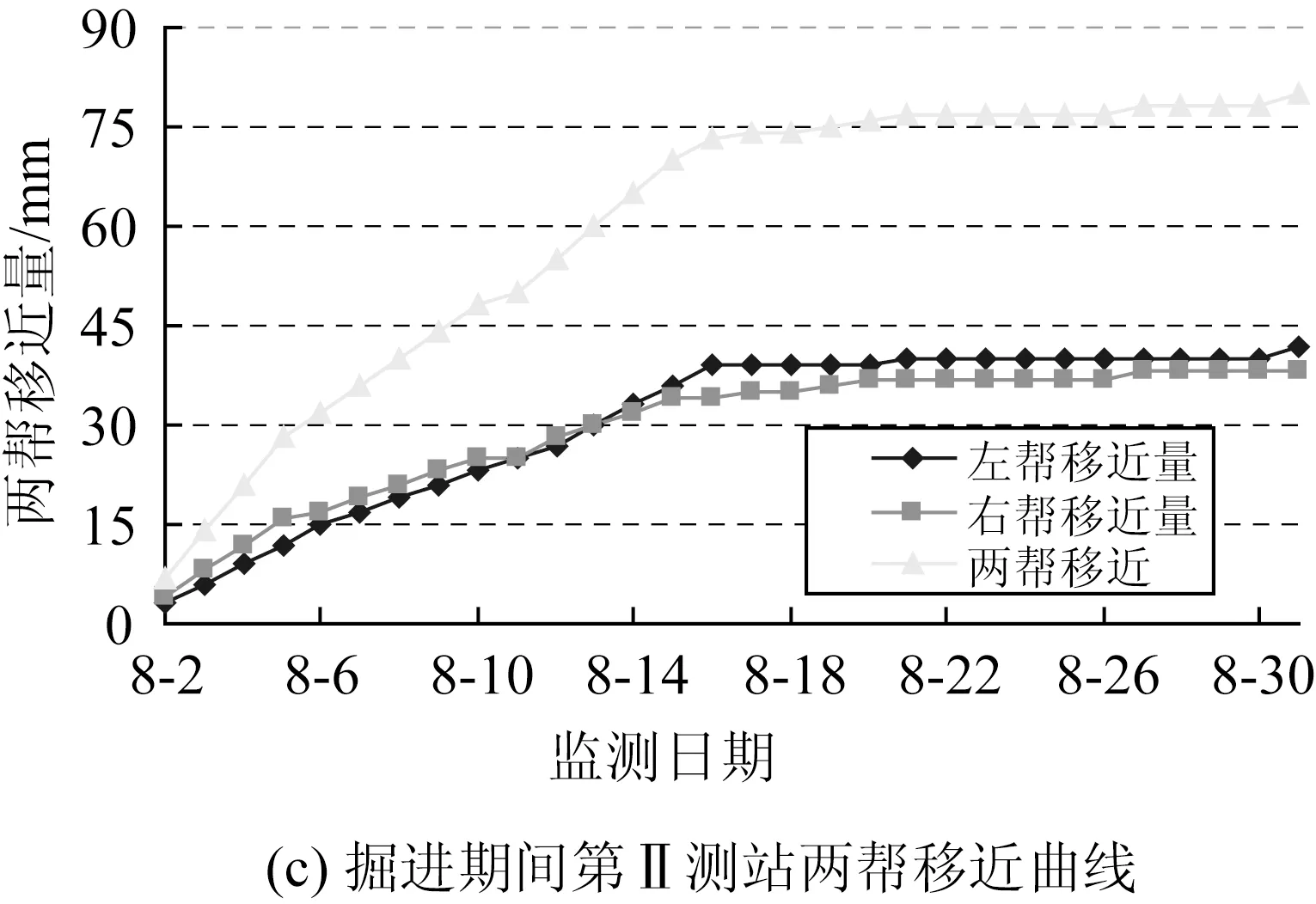
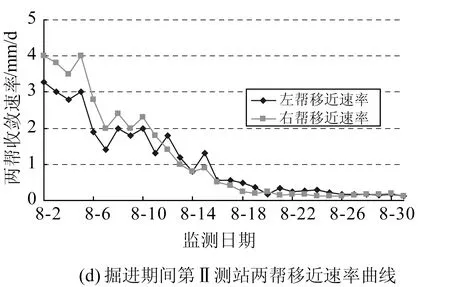
圖4 掘進期間第Ⅱ測站圍巖收斂曲線

[1] 蘭永偉, 張永吉，等. 深部開采條件下巷道底臌機理的研究[J]. 礦業研究與開發，2005，25(1).

[2] 何滿潮. 中國煤礦軟巖巷道支護理論與實踐[M],徐州: 中國礦業大學出版社, 1996:112-117.

[3] 董方庭. 巷道圍巖松動圈支護理論及其應用技術[M]. 北京: 煤炭工業出版社, 2001.

[4] 王希良,彭蘇萍,杜木民．三軟煤層頂板工程地質分類及變形機制[J]．礦山壓力與頂板管理,2005(2):49-52.

[5] 何滿潮, 景海河, 孫曉明. 軟巖工程力學[M]. 北京: 科學出版社, 2002.