基于神經網絡和遺傳算法的公差優化設計

趙 罡 王 超 于紅亮

(北京航空航天大學 機械工程及自動化學院,北京 100191)

基于神經網絡和遺傳算法的公差優化設計

趙 罡 王 超 于紅亮

(北京航空航天大學 機械工程及自動化學院,北京 100191)

針對產品制造中公差與成本之間高度非線性關系的特點,提出了一種綜合神經網絡與遺傳算法進行公差優化的方法,該方法利用遺傳算法在大范圍解空間內采用概率搜索策略得到全局最優解且有較強魯棒性的特點,以及神經網絡解決高度非線性問題的優越性,首先利用神經網絡對公差成本進行仿真,得到具有黑箱特點的公差成本函數關系;然后在公差分配中采用遺傳算法,以總成本最小為目標函數,以滿足裝配公差要求和符合標準公差等級為約束條件進行優化;同時基于 VC和 Matlab開發了公差優化系統,以飛機艙門鎖鉤機構為對象進行了驗證,并針對不同的公差成本及分配方法進行了對比.結果表明:采用神經網絡與遺傳算法綜合分配的結果與傳統方法相比具有較大的優越性.

公差成本關系;公差優化;神經網絡;遺傳算法

公差設計包括公差分析與公差綜合兩個部分.公差綜合(tolerance synthesis)也叫公差分配(tolerance allocation),是指在保證產品裝配技術要求下規定各組成環尺寸經濟合理的公差[1].在進行公差分配時,需要綜合考慮零件的產品功能、尺寸大小、幾何形狀、材料性能、現場設備、工藝方法與制造成本等多方面因素.因此,公差分配可以有多種不同的公差分配方案,是一個相當復雜的多解問題.

公差設計的發展已經經歷了 1個多世紀,但直到 1978年,文獻[2]中提出利用計算機輔助確定零件的幾何形狀、尺寸和形位公差的概念,用數學方程式來描述零件的幾何形狀,并以此來進行零件的尺寸和公差設計.從此計算機輔助公差設計(CAT,Computer Aided Tolerancing)得到了廣泛的關注.1988年,文獻[3]提出將公差需求從設計階段傳遞到制造階段的方法來解決工藝設計中的公差問題,由此掀起了 CAT研究的高潮,隨后CAT的研究進入了大發展期.

在公差綜合方面國內外學者已經進行了較多的研究.文獻[4]提出了基于規則的綜合,給出了各種常用的公差綜合理論及方法;文獻[5-6]提出了公差魯棒設計和相應的確定性算法;文獻[7]提出了基于 BP神經網絡的成本-公差模型;文獻[8]對加工質量進行了公差分配,并提出了一種基于遺傳算法的方法.國內方面,文獻[9]提出了基于裝配成功率的公差優化設計方法;文獻[10]提出了基于群集智能的產品公差優化設計方法,利用粒子群的方法進行多目標綜合優化.

這些研究極大地拓展了 CAT研究的廣度,但對于一些公差-成本關系復雜的模型來說,用傳統的公差-成本模型來仿真擬合,然后再用構造的優化模型分配裝配體中各個零件的公差量,其結果往往會誤差很大,無法得到滿意的優化結果;而把公差-成本模型與公差優化模型作為一體來綜合考慮將會很好地解決這一問題.

考慮到公差優化是加工制造中的公差-成本模型及公差優化分配兩部分的組合過程,本文提出將基于 BP神經網絡和遺傳算法結合在一起對公差進行優化分配的方法,并以飛機艙門鎖鉤機構作為實例對該方法進行了驗證.

1 公差-成本模型

對于公差優化設計來說建立一個具有實用性的模型是至關重要的,因為模型對公差分配的實際應用起關鍵作用.由于各種零件的幾何形狀,尺寸及材料都有所不同,則其制造中所產生的成本也將不同,因此,一旦考慮到零件的加工材料、加工尺寸以及加工方法等,就很難用一個精確的數學模型來完整地描述公差與成本之間的關系.一般來講,公差越小,所需要的加工成本便越大,反之則成本將越小.為了有效地表述公差與加工成本之間的關系,本文設定零件材料為鋁合金,以中等批量零件加工時所用的切削用量和加工設備(主要是數控機床)為基準,以平面加工特征為研究對象,對公差及加工成本進行仿真.

1.1 傳統公差-成本模型

對于公差成本模型的研究,已經有了大量的研究結果,提出了較多的公差-成本模型,如傳統的指數模型、負平方模型、倒數冪指數模型等[7].這些模型的共同點是:在某特定的加工環境下,采集足夠的公差成本的統計數據,然后用最小二乘法等優化方法確定模型中的參數.

但是,這些傳統的公差-成本模型無法完整準確地描述公差成本之間復雜的數學關系.而神經網絡方法在解決高度非線性問題方面具有很強的優越性,而且擬合誤差可以控制在一個極小的范圍,通過給定少量的訓練樣本作為輸入和輸出就可以很好地反映出輸入輸出間的關系.因此用神經網絡來描述公差-成本模型就比較合適.

1.2 BP神經網絡建立公差-成本模型

本文采用改進 LM(Levenberg-Marquardt)算法來訓練 BP神經網絡,從而模擬公差與成本之間的對應關系.基于 LM算法的 BP網絡克服了BP算法隨著迭代次數的增加,梯度下降逐漸變小,從而收斂速度較慢的問題,可以減少迭代次數,加速網絡的收斂.

所需要確定的參數主要有:所用網絡的層數、各層神經元的個數、各層的傳輸函數以及網絡的學習算法.

1)網絡的層數.研究[11]表明:如果 BP網絡中隱層神經元數可以根據需要自由設定,那么一個 3層網絡可以實現任意非線性映射.考慮到本模型對精度要求較高,因此采用含有輸入層、隱層和輸出層 3層的 BP神經網絡.

2)各層神經元個數.一個具有無限個隱層神經元的 3層 BP網絡可實現任意從輸入到輸出的非線性映射,但對于有限個從輸入到輸出的映射,并不需要無限個隱層節點.對于隱層節點個數的選擇,至今為止,還沒有找到一個很好的解析式,而是根據經驗來確定節點個數,參數公式[11]為

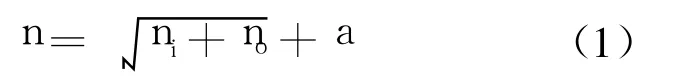
其中,n為隱層節點個數;ni為輸入節點的個數;no為輸出節點的個數;a為 1～10之間的常數.

本文中輸入節點為公差及其對應的工序類型,節點數為 2,輸出為其對應的成本,節點數為1,得到隱層節點的個數為 n=10.

3)網絡各層的傳輸函數.一般情況下,具有3層的 BP網絡,隱層采用 Sigmoid類型的轉換函數,而輸出層則根據輸出結果的范圍選取,另外,為了在訓練時能夠使網絡較快地達到穩定狀態(即能夠使網絡的權值與閾值能夠得到較快的調整),本文選取 tansig函數作為隱層傳輸函數,logsig作為輸出層傳輸函數.為了提高訓練速度和靈敏性及有效避開 Sigmoid函數的飽和區,需要對輸入及輸出數據進行歸一化處理.由于生產過程中公差并不是均勻分布的,因此,本文對公差的歸一化方法[8]為

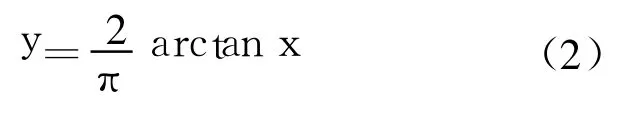
其中,x為公差原始值;y為歸一化之后的值.

4)系統模型.本系統所用的網絡模型見圖 1.

1.3 利用神經網絡仿真

利用神經網絡進行優化需要有對應的公差及成本數據作為專家樣本來訓練網絡,而現實中工廠是以工序為單位進行生產,而以工時為單位來衡量成本的大小,公差與成本的數據難以統計,因此本文采用了文獻[12]的數據作為優化用的樣本數據.

基于 Matlab和 VC平臺,開發了神經網絡仿真公差-成本模型,其中 Matlab與 VC的混合編程的方式包括基于 MatCom,將 Matlab代碼編譯為dll或可執行程序,以及采用 Matlab Engine和Matlab的 C/C++數學庫等 5種方法.

本文采用 VC調用 Matlab生成的動態 dll庫的方法,通過將 Matlab神經網絡工具箱的函數打包成 d ll然后在 VC里調用,圖 2所示為對公差-成本的樣本數據采用 BP網絡進行訓練的過程.

圖1 公差-成本神經網絡圖

圖2 VC調用Matlab進行神經網絡訓練

2 基于遺傳算法的優化

其中,T∑表示封閉環的公差;n表示環的個數;Ti(i=1,2,…,n-1)表示各組成環的公差.

當 T∑ 已知,而 Ti未知時,式(3)為不定方程,有無數組解.考慮到不同的側重,如加工精度、

2.1 傳統分配方法

極值法情況下封閉環與組成環的公差關系為工序能力等,解決這個問題的傳統方法有等公差法、等精度法、等工序能力法等.

這些傳統的分配方法過于簡單,只適用于公差設計初期,可得到簡單的公差分配結果,而遺傳算法不僅能收斂到全局最優解,而且具有較快的收斂速度,算法優化效率高,魯棒性強,更適合于獲得全局最優的公差分配結果.

2.2 遺傳算法公差優化分配

本文需要優化的是各組成環的尺寸公差,在其滿足標準公差等級的要求,同時還需要保證相應封閉環的技術要求的前提下,使得各組成環的加工成本最低,即

其中,ITj表示各組成環優化后的公差等級是否為IT j,如果所選取的等級為 j,則 ITj=1,否則,ITj=0;STj表示公差等級為 j時組成環對應的標準公差值;f(T1,T2,…,Tn-1)表示各組成環公差與封閉環公差之間的關系式,根據技術要求不同,其值也不同.在考慮裝配成功率滿足 6σ法則時:

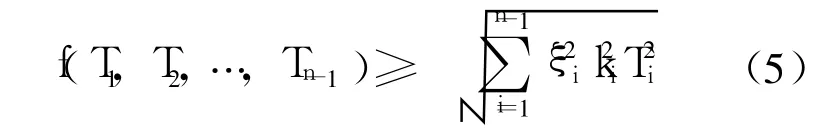
通過采用遺傳算法,將標準公差等級編碼,同時加入罰函數以表示相應的約束條件,將公差成本作為適應度函數值,可以較為方便地解決這一問題.

1)標準公差等級編碼.編碼就是將問題的解用一種碼來表示,從而將問題的狀態空間與 GA的碼空間相對應.通過 GA搜索得到符合要求的最優解的編碼而將其對應到問題的表現.研究[13]表明,采用二進制編碼方案能包含最大的模式數,使得遺傳算法在確定規模的群體中能夠處理最多的模式.

本文采用二進制編碼的方式,以各個組成環公差等級編號組合作為最后的編碼.每個組成環公差等級編號由 3位二進制碼組成.

總的編碼長度為

總的編碼方式為

其可能的組合方式有 23×23×…×23=(23)(n-1)種.其中,每個組成環有 8種備選公差等級:IT 5～IT 12,于是一個具有 5個組成環的尺寸鏈,其個體的編碼為,其中每個字符代表 0或 1,則一個編碼為 011010000100的個體解碼后所表示的意義如表 1所示.

表 1 個體解碼的意義

2)約束條件的轉換.根據式(4),本文中所要解決的問題包含 2個約束條件,針對這 2個約束條件,本文采用了 2種不同的處理方法:

①用編碼的方法來保證產生出的個體總是在可行解空間之內.如針對公差等級 IT 4～IT 11共 8個等級,分別以 000～111予以對應.這樣就解決了第 1個約束條件:

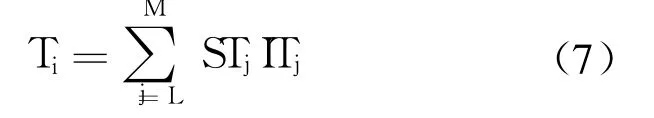
②通過加入罰函數的方法,降低不在解空間里的個體的適應度,從而降低該個體遺傳到下一代群體中的概率.

其中,FC(x)表示修正之后的適應度函數;P(x)表示所選取的罰函數.

本文選取 P(x)=F(x)來作為罰函數,使得不滿足要求的個體遺傳到下一代群體中的概率為0,這樣雖然降低了群體的多樣性,但是卻加快了算法的收斂速度.經實例驗證,該方法設定罰函數是有效的.

2.3 系統工作流程

基于以上理論方法,采用 VC調用 Matlab生成的動態dll庫的方法,開發了遺傳算法優化公差的系統,在其中調用了神經網絡優化得到的公差數值,完成了基于神經網絡和遺傳算法的公差優化設計.整個系統的工作流程如圖 3所示.

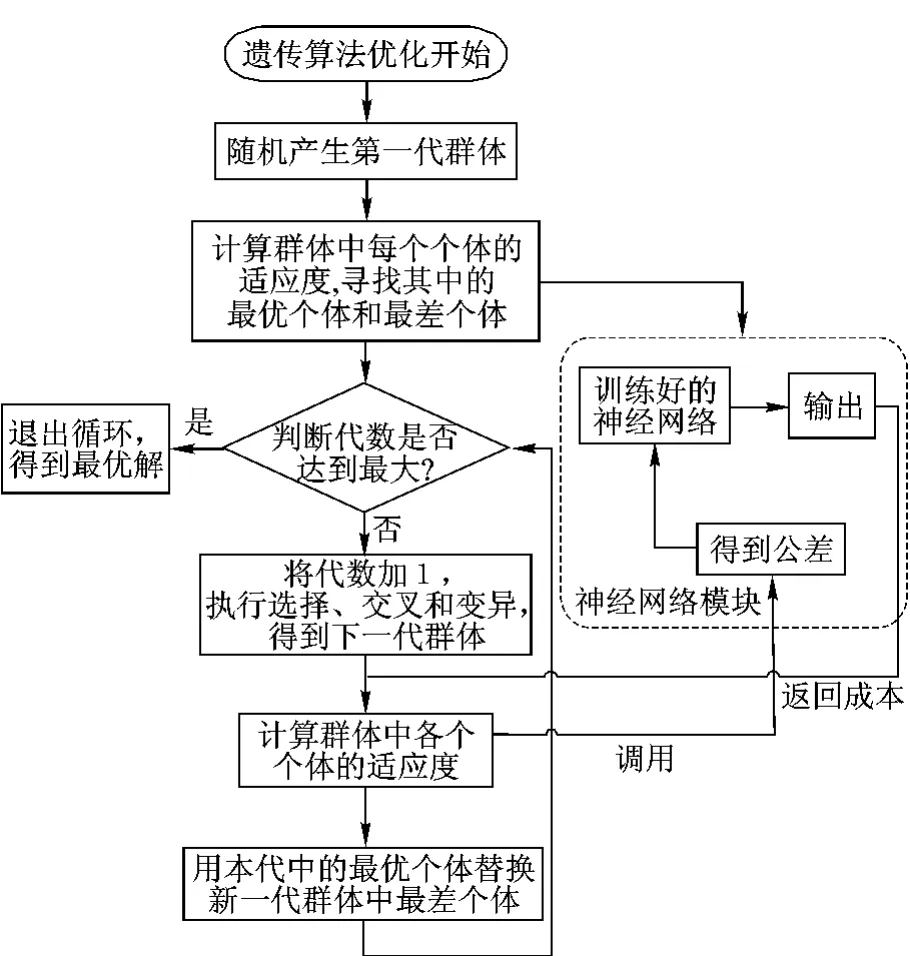
圖3 系統工作流程圖

3 實例分析

3.1 實例說明

本實例以飛機艙門中鎖鉤機構的公差設計為研究對象,通過對其進行公差分配來驗證所提出算法的可行性以及采用神經網絡和遺傳算法進行公差分配的優越性.圖 4所示為艙門運動機構組件中鎖軸和鎖鉤組件裝配部分圖,圖 5為其對應的尺寸鏈.為了保證鎖鉤處于打開或者關閉狀態都能夠平滑地運動,需要檢查鎖鉤與偏心襯套之間的間隙尺寸 A0.根據設計要求,間隙 A0應該在4.00～4.75mm范圍內.

圖4 艙門鎖鉤機構圖

圖5 相應的尺寸鏈

各零件的基本尺寸為:A1=A4=34.0mm,A2=28.5mm,A3=10.5mm,A5=111.0mm,對應的尺寸鏈方程為

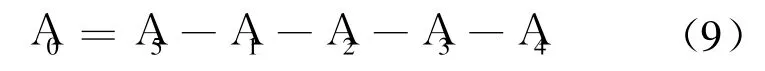
以式(4)的總成本最小為目標函數.通過Matlab對公差成本以指數形式擬合,得到結果為

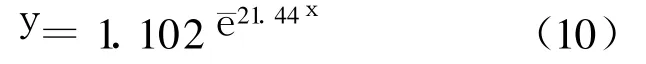
其擬合圖像如圖 6所示.

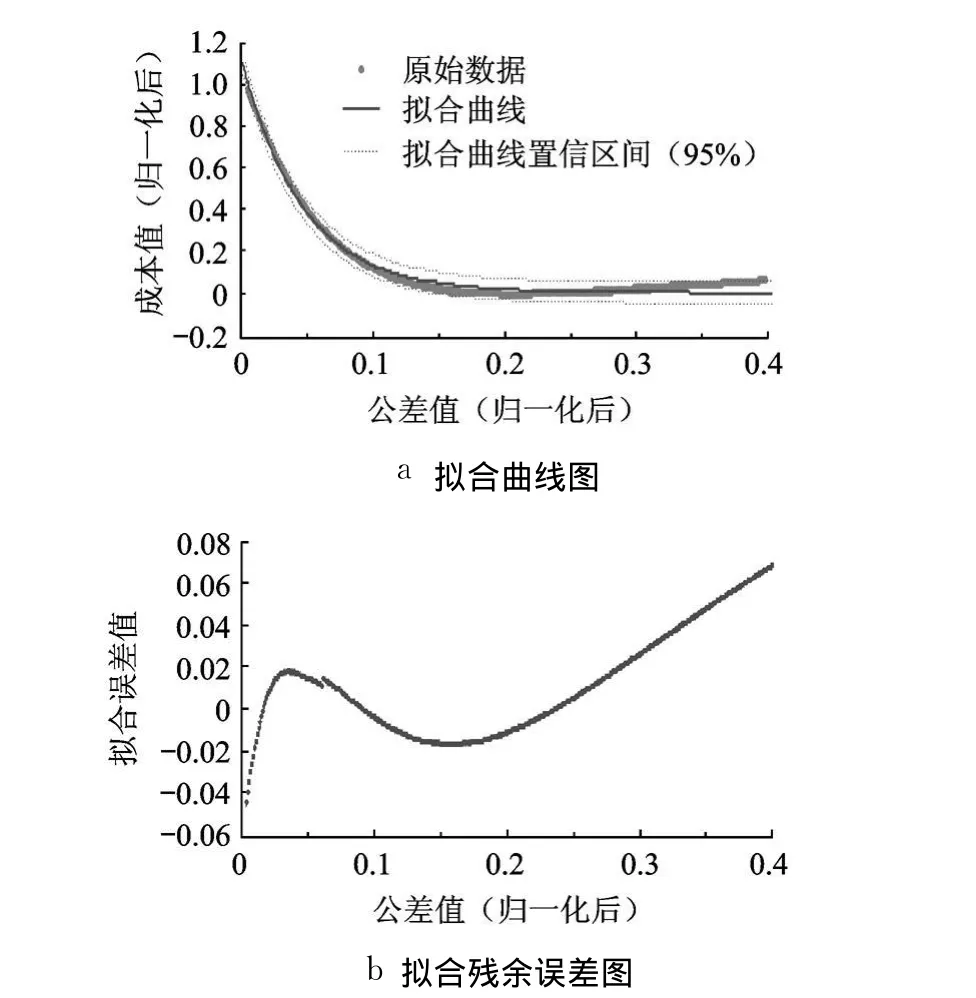
圖6 擬合指數形式的公差成本曲線

3.2 實驗結果對比

本文采用了神經網絡和指數法分別得到的公差成本模型以及公差分配分別采用遺傳算法和等公差法,以 3種方法組合為例:神經網絡與遺傳算法結合、神經網絡與等公差法結合、指數法與等公差法結合.對所分配得到的公差和成本結果進行比較,采用 3種組合方法求得的公差值和總成本(歸一化后)的數據結果如表 2所示.

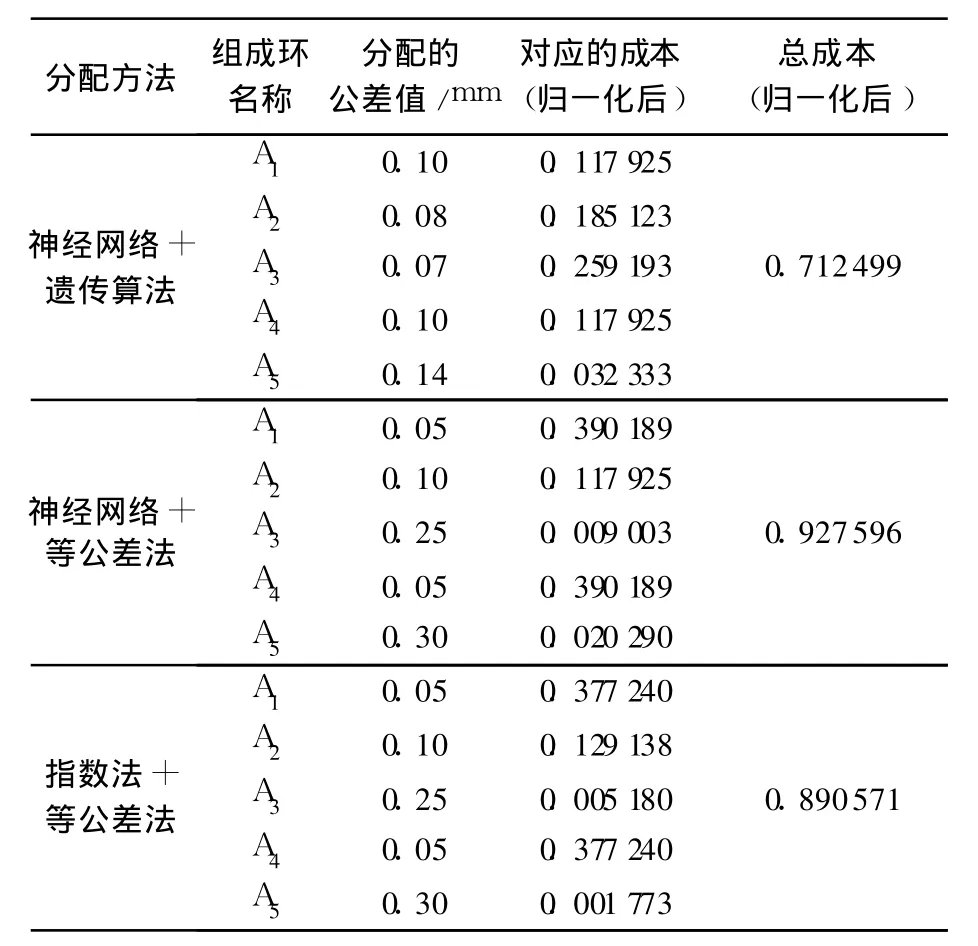
表 2 各種方法得到的公差值和成本對比

3.3 實驗結果分析

由表 2的結果可知,采用遺傳算法與神經網絡結合的方法得到的總公差成本與其它 2種相比,分別降低了 30.189%和 24.993%,達到了較好的效果.

4 結 論

本文綜合利用了神經網絡與遺傳算法各自的特點來解決公差優化中公差-成本關系和公差分配 2個問題.利用神經網絡對公差成本進行仿真,得到具有黑箱特點的公差成本函數關系,在此基礎上以最小成本為目標函數,以滿足裝配公差要求和標準公差為約束條件,利用遺傳算法進行優化,并通過實例驗證了該方法的可行性,結果表明,采用本方法進行公差分配可以明顯降低產品的成本.

References)

[1]吳昭同.計算機輔助公差優化設計[M].杭州:浙江大學出版社,1999:3-6 Wu Zhaotong.Computer aided tolerance optimization design[M].Hangzhou:Zhejiang University Press,1999:3-6(in Chinese)

[2]Hillyard R C.Dimensions and tolerances in shape design[D].Cambridge:Computer Laboratory,University of Cambridge,1978

[3]Weill R,Clement R,Hocken R.Tolerancing for function[J].CIRP Annals-Manufacturing Technology,1988,37(2):603-610

[4]Raman S,PanchalK,SiminpulatP.Computer aided tolerance assignment[J].Computers＆Industrial Engineering,1991,21:67-71

[5]Parkinson D B.Robust design by variability optimization[J].Quality and Reliability Engineering International,1997,13:97-102

[6]Parkinson D B.The application of a robust design method to tolerancing[J].Journal of Mechanical Design:Transactions of the ASME,2000,122:149-154

[7]Lin Z C,Chang D Y.Cost-tolerance analysis model based on a neural networks method[J].International Journal of Production Research,2002,40(6):1429-1452

[8]Forouraghi B.Worst-case tolerance design and quality assurance via genetic algorithms[J].Journal of Optimization Theory and Applications,2002,113(2):251-268

[9]楊將新.基于裝配成功率的公差優化設計系統研究[D].杭州:浙江大學機械工程學系,1996 Yang Jiangxin.Study on computer-aided tolerance optimum design based on stack-up yield[D].Hangzhou:Department of Mechanical Engineering,Zhejiang University,1996(in Chinese)

[10]肖人彬,陶振武,鄒洪富.基于混合群集智能算法的并行公差優化設計[J].計算機集成制造系統,2007,13(4):668-674 Xiao Renbin,Tao Zhenwu,Zou Hongfu.Concurrent tolerance optimization design based on hybrid swarm intelligence algorithm[J].Computer Integrated Manufacturing Systems,2007,13(4):668-674(in Chinese)

[11]周開利,康耀紅.神經網絡模型及其 MATLAB仿真程序設計[M].北京:清華大學出版社,2005:75-94 Zhou Kaili,Kang Yaohong.Neuralnetworkmodel and MATLAB simulation programming dsign[M].Beijing:Tsinghua University Press,2005:75-94(in Chinese)

[12]楊將新,顧大強.基于神經網絡的機械加工成本-公差模型[J].中國機械工程,1996,6:41-42 Yang Jiangxin,Gu Daqiang.Machining cost-tolerance model based on artifical neural network[J].China Mechanical Engineering,1996,6:41-42(in Chinese)

[13]周明,孫樹棟.遺傳算法原理及應用[M].北京:國防工業出版社,1999:32-40 Zhou Ming,Sun Shudong.The genetic algorithms:algorithms and applications[M].Beijing:National Defense Industry Press,1999:32-40(in Chinese)

(編 輯:文麗芳)

Tolerance optimization based on neural network and genetic algorithm

Zhao Gang Wang Chao Yu Hongliang

(School of Mechanical Engineering and Automation,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Taking into account the highly non linear relationship between the cost and the tolerance in the product manufacturing process,a method based on the neural network in conjunction with the genetic algorithm was proposed to solve the tolerance optimal issues.The method integrates the advantage of the genetic algorithm,which can obtain the optimal result in a large-scale solution space using the probability searching strategy and the strong robustness,and the superiority of the neural net work that can solve the highly nonlinear problem.In the optimization process,the neural network was trained using sample data to simulate the tolerance-cost function at first and geta function relationship with the black box feature between the cost and the tolerance.And then the genetic algorithm was introduced to optimize the tolerance allocation by taking the results of the trained neural network.It takes the functional requirements and the standard tolerance grades as constraints as well as the minimum of the component cost as the objective.A tolerance optimization system based on a C++library and the Matlab was designed.Finally,an example of the latching shaft and hook mechanism component of the aircraft cargodoor demonstrated the method.The analytical result proves that the new method can produce the tolerance optimization economically and accurately,and has an advantage over traditional methods.

tolerance-cost function;tolerance optimization;neural network;genetic algorithm

TP 391

A

1001-5965(2010)05-0518-06

2009-12-15

國家 863計劃資助項目(2007AA 041902)

趙 罡(1972-),男,河北文安人,副教授,zhaog@buaa.edu.cn.