帶條件風險約束的發電商最優投標模型及計算＊

羅 可,趙志學,童小嬌

(1.長沙理工大學計算機通信工程學院,湖南長沙 410076;2.湖南商學院計算機與電子工程學院,湖南長沙 410205)

在電力市場中,發電商投標策略模型和計算方法的研究得到了國內外學者的廣泛關注.文獻[1]對投標策略的研究進行了比較全面的介紹,按研究方法的不同可分為3類:其一是通過預測下一交易日的市場清除價格來制定投標策略的方法,該方法適合于小型發電商且其投標策略對市場淸除價格基本沒有影響的情形;其二是基于博弈論求解市場均衡的方法,該方法在發電商不具備完全的市場信息時缺乏有效的處理手段,導致最終投標策略脫離現實;其三是估計其他競爭對手投標行為的方法,該方法需要對其他競爭對手的投標策略的分布函數進行估計,最終確定自己的投標策略.

通常,期望利潤大的投標策略其風險也大.因此,發電商需要對投標策略的風險進行分析和評估,構造兼顧期望利潤最大和風險最小兩個矛盾目標的折衷投標策略.鑒于此,已有大量的學者將風險分析方法應用于投標策略的研究.文獻[2]Markowitz第一次從風險資產的收益率與風險之間的關系出發,用方差來描述風險,討論了不確定性經濟系統中最優資產組合的問題.然而,該模型用方差計量風險有較大的局限性.20世紀90年代Value-at-Risk(VaR)成為風險管理的主要手段.Alexander G和Baptista A[3]提出的以VaR作為風險函數的“均值-VaR”模型.Rockafellar-Uryasev等[4]在2000年分析了VaR方法在實際應用中的缺陷,并提出條件風險(Condition Value-at-Risk:CVaR)作為風險的度量.與VaR比較,CVaR滿足風險度量的一致性特點,可運用于一般的隨機變量分布;特別是通過引入一個特殊的輔助函數,使CVaR可用凸優化計算,同時得到VaR的值.CVaR作為風險度量的這些優點使其應用日益廣泛,許多學者進行了深入的研究[5-13].

本文探討將CVaR理論應用于電力市場領域.基于電力市場的運營機制和投標方法[14-15],本文構造了一種基于CVaR發電商最優投標策略的新模型,應用第3類方法——估計其他競爭對手投標行為制定投標策略,對對手的投標數據參數采用了蒙特卡洛仿真模擬,提出了求解發電商最優投標策略模型的PSO(Particle Swarm Optimization,PSO)算法,保證了算法的全局收斂性.IEEE多個算例的數值顯示本文所提出的模型和算法具有較好的計算效果.

1 CVaR模型簡介

記x∈X?Rn為決策變量,隨機變量y∈Rm的分布為p(?),通常定義f(x,y)為損失函數.在文獻[4]中,Rockafellar-Uryasev定義條件風險CVaRβ(x)為:

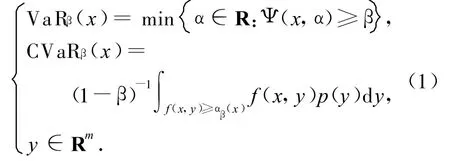
其中:β為置信水平,VaRβ(x)為風險值.文獻[4]通過構造函數Fβ(x,α)來計算CVaRβ(x),其中:

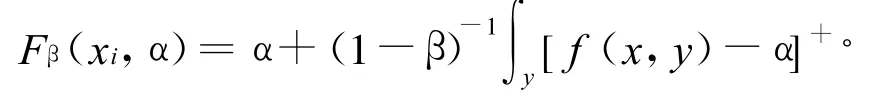
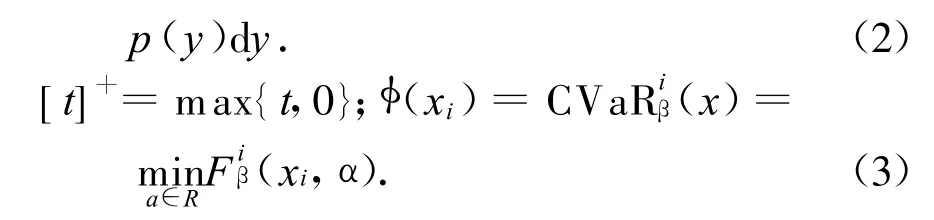
文獻[4]還證明了Fβ(x,α)是關于變量α的連續可微凸函數.因此CVaR為一凸規劃問題的最優值.由于式(2)是連續性的,需要對其進行離散化,用的近似值代替它,得到式(4):

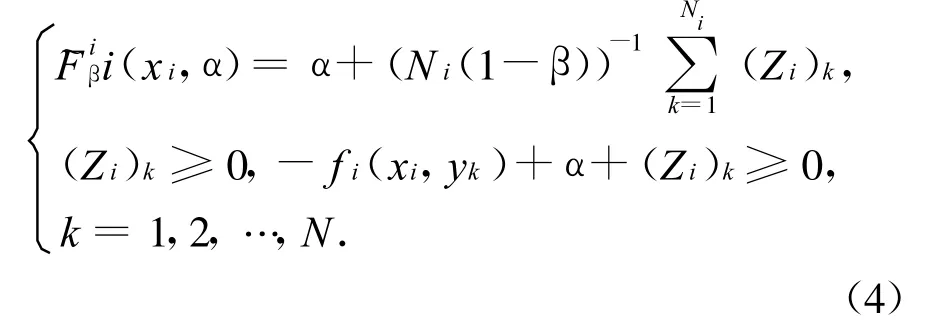
2 發電商最優投標模型

假設電力市場包括n家發電商,每一個發電商只有一臺發電機組,給定投標函數為:

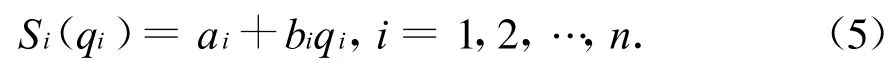
記(xi,x-i)=((ai,bi),(a-i,b-i)),其中ai,bi為所求發電商的投標參數,a-i,b-i為競爭對手的投標參數,qi為發電量.發電商的成本函數為:

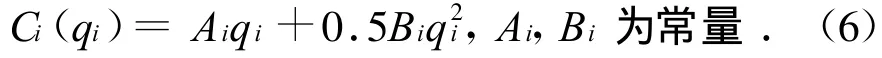
發電商的利潤函數為:

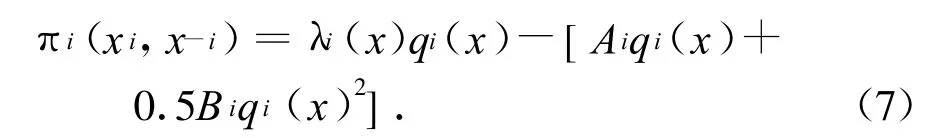
其中:λi,qi分別是結點i的價格和發電量,它們分別為發電商投標后綜合考慮社會效率最大化或費用最小化確定的價格和電量分配,可由ISO模型求出.假定以第i家發電商為研究對象,其競爭對手服從正態分布.

ISO模型是在考慮社會效益最大化和網絡約束的條件下進行最優調度.其模型表達式為:

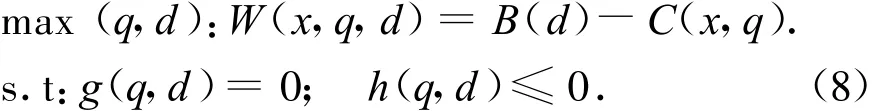
其中:

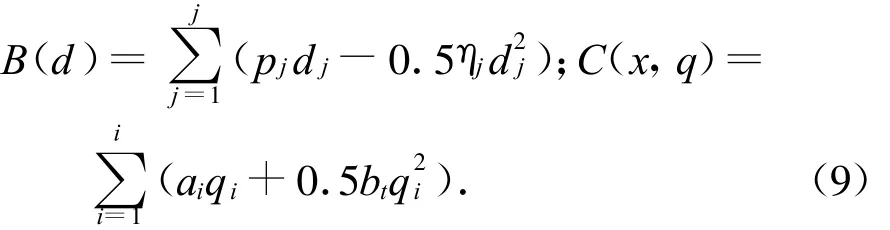
d=(d1,d2,…,dj)為用戶(網絡)的需求,q=(q1,q2,…,ql)為發電商的發電量,B(d)為效用函數,C(x,q)為發電商的總成本函數.h(q,d)為系統運行約束和發電機出力約束,因此定義KKT系統為:

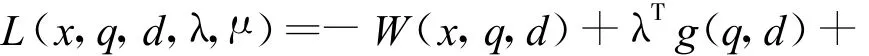
利用式(10)求解出利潤函數中的發電電量q,用戶需求d和市場清除價λ.

根據利潤函數的期望來求解最大利潤,由此可知第i個發電商最優投標模型可以表示為:

由于式(11)中的約束條件φ(xi)≥Vi中設置f(x,y)為利潤函數的相反數,可以由式(4)和式(10)得到,由此得出總投標模型為:

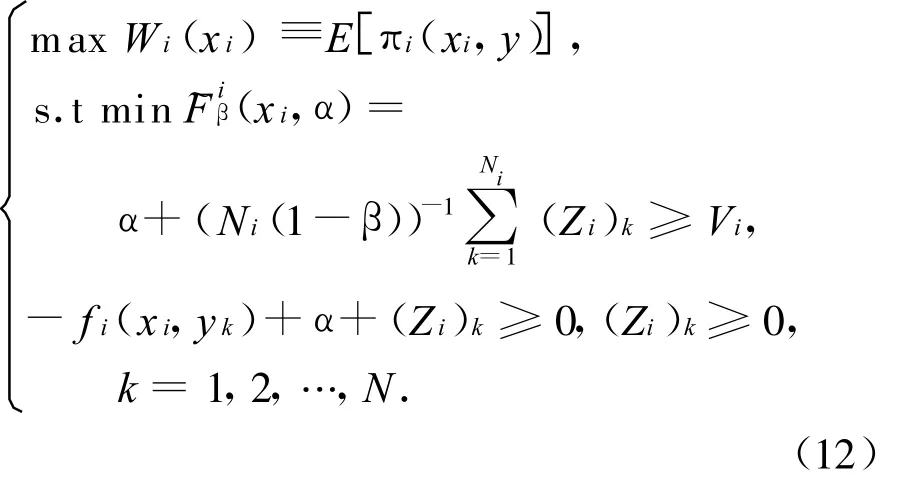
3 算法設計

PSO算法是Kennedy和Eberhart博士于1995年提出的一種基于群體智能的進化方法.基本的粒子群模型在一個n維的空間內,m個粒子組成的群體與進化代數t相關的粒子位置及速度構成,表示為=(,,…,…,)=(,…,,…,)式中:j=1,2,…,m,為粒子的編號;i=1,2,…,n,為粒子位置元素的編號;t為進化的代數.因此在t+1代,粒子j的速度更新表達式為:

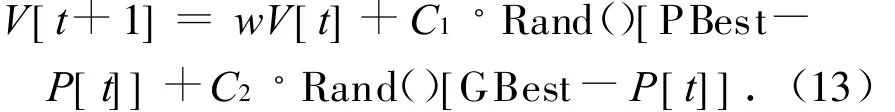
粒子j位置的更新表達式為:

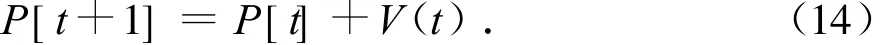
C1,C2為常數,Rand()為在[0,1]區間均勻分布的隨機數.

ISO優化模型是一個典型的二次凸規劃問題,可用一般優化算法進行最優值的求解.CVaR模型是一個線性規劃問題,可以用PSO算法進行計算,并且具有全局收斂性.

PSO算法隨機產生粒子,每個粒子代表發電商待優化參數,從樣本數據中選擇規定范圍內N個粒子Xi,再對每個產生的粒子進行ISO優化調度.根據文獻[14]提出的“3σ規則”,對競爭對手的投標進行估計,隨機抽取k個點進行模擬,得到k個相應的f和相應的(λi,qi),然后代入CVaR模型求解.在計算粒子適應度之前,需要驗證粒子位置變量是否違反約束,以決定是否對粒子適應值進行懲罰.其適應度為:式中:r為懲罰項,c1,c2和c3為正常數.具體的算法步驟為:

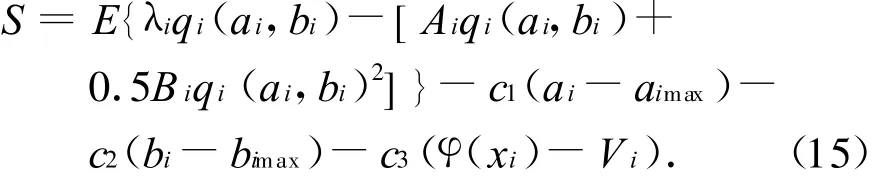
Step1 初始化粒子,粒子為2維數組(Swarm[ai,bi]),粒子數為N,最大迭代次數為Tmax,精確度閥值為eps,式(13)中的C1和C2取值為1.496 2.在規定范圍內隨機產生粒子位置和速度信息.

Step2 對競爭對手的投標參數系數[a-i,b-i]進行蒙特卡洛模擬仿真,取k個yk.

Step4 將每個粒子代入到適應度函數(15)中,求解適應度.若該適應度值好于歷史最好值(Pbest),則令當前值作為新的Pbest,在所有的Pbest中選取最優的作為全局最優點(Gbest).

Step5 利用式(13)和式(14)更新粒子的速度和位置.

Step6 判斷是否達到迭代終止條件——一個預設的最大迭代次數Tmax(t≥Tmax)和最小精度閥值eps為粒子數),則程序終止,否則t→t+1,返回Step3,進行新一輪的迭代.

4 數值實驗

4.1 IEEE4-bus不同V下的效益以及各項結果

首先采用IEEE4-bus系統對所提出的方法進行測試,模擬電力傳輸網絡數據進行計算.圖1為4節點2發電機系統的結構圖,1,2號節點各有一臺發電機;而3,4號節點是負荷節點.表1為發電商技術與經濟參數表和ISO負荷需求參數表.

為了簡潔,采用直流潮流約束進行計算,通過修改各線路的阻抗和容限來調整發電機的發電量、負荷節點的電量和電價。假定以2號發電商為研究對象,其中C=19,β=95%,引用文獻[13]的計算結論,A2的搜索范圍為[0.5＊3,10＊3],B2的搜索范圍[0.5＊0.025 00,10＊0.025 00],同時假設q,d相等.通過計算,當V=25時,其最優投標系數a2=5.159 8;b2=0.400 1;q1,q2,d1,d2=(0.462 4,4.598 8,2.326 2,2.735 0)MW;這時的市場清除價R=6.999 8美元/(MW?h),利潤為18.129 8美元.

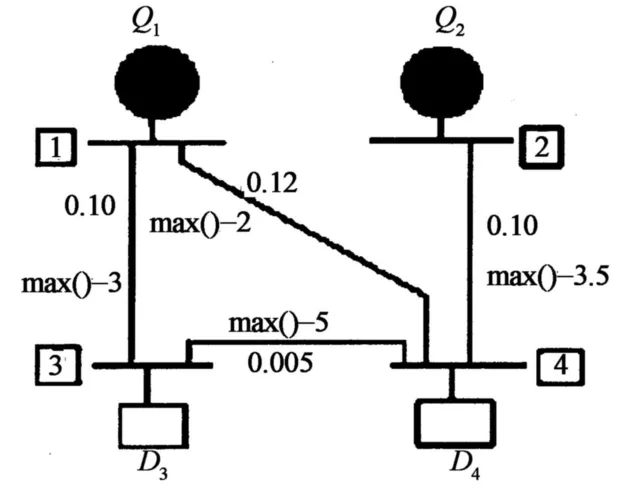
圖1 4節點2發電機結構圖Fig.1 4 node 2 generator structure chart

表1 發電商的技術和經濟參數表和負荷節點參數表Tab.1 Technical and economic parameters table

表2,表3分別為發電商1和2在給定不同的V時所求得的最優投標系數ai,bi、市場清除價λi以及利潤Maxπ.從表3的計算結果可以看出,隨著V的降低,最優投標系數a2,b2變大,即投標系數增加,被調度的發電量q相應增大,利潤的期望值f隨之增加,市場清除價也有小幅度增長.當V達到一個特定值以后,最大利潤也趨于平衡,最后達到一個穩定的值.

表2 發電商1在不同V下的最優投標系數以及結果Tab.2 The 1st generation company's resultfor a given different V

由于設置f(x,y)為利潤函數的相反數,所以VaR,CVaR是一個負數,為了方便,采用-VaR,-CVaR進行說明.如果盲目追求利潤而采用較高的報價系數,雖然所得的期望利潤會相應的變大,但是-VaR和-CVaR值小于期望值,高報價的相應風險也會增大.此外,還可以看出-CVaR的值一般都小于-VaR值,這是由于CVaR反映的是收益尾部α分位點之后的期望值,也就是考慮了最壞情況中的所有情況,因此-CVaR值小于-VaR值,它比-VaR值更準確地度量了發電商的風險.

表3 發電商2在不同V下的最優投標系數以及結果Tab.3 The 2st generation company's result for a given different V

圖2為4節點2發電機系統效益前沿圖,從圖2可以看出,兩家發電商在不同的V下的最大期望利潤都是單調遞增一段以后達到平衡.

從以上比較分析可得,不同的V值能直接導致不同的投標系數,調度的發電量,以及市場清除價格和發電商的利潤.如果忽略風險因素,會直接影響自己的投標決策,達不到預期利潤從而產生損失,所以在制定投標策略時必須考慮相應的風險.同樣,求解發電商1的結果,從中可以看到由于輸電量的約束導致-V足夠小的時候q1只能趨向3.82;其他變量的變化同第2家發電商,當-V變大時,最優投標系數a1,b1變大,被調度的發電量相應增加,利潤的期望值也隨之增加,市場清除價也有小幅度增大.

通過數值實驗統計粒子迭代收斂的動態信息,可以得出粒子位置和速度的演化進程從而可以了解最優解的求解過程.以求解發電商2為例,在V=15時跟蹤粒子2的位置和速度變化情況.對于粒子2(x2-(a2,b2)),a2其速度值在前49代中是在0上下振蕩的,對應的位置在5.1附近振蕩.在這之后,粒子的位置穩定在5.15,而速度穩定在0;b2其速度值在前47代中是在0上下振蕩的,對應的位置在0.40附近振蕩.在這之后,粒子的位置穩定在0.398 7,而速度穩定在0,這表明所求的結果是全局最優解.

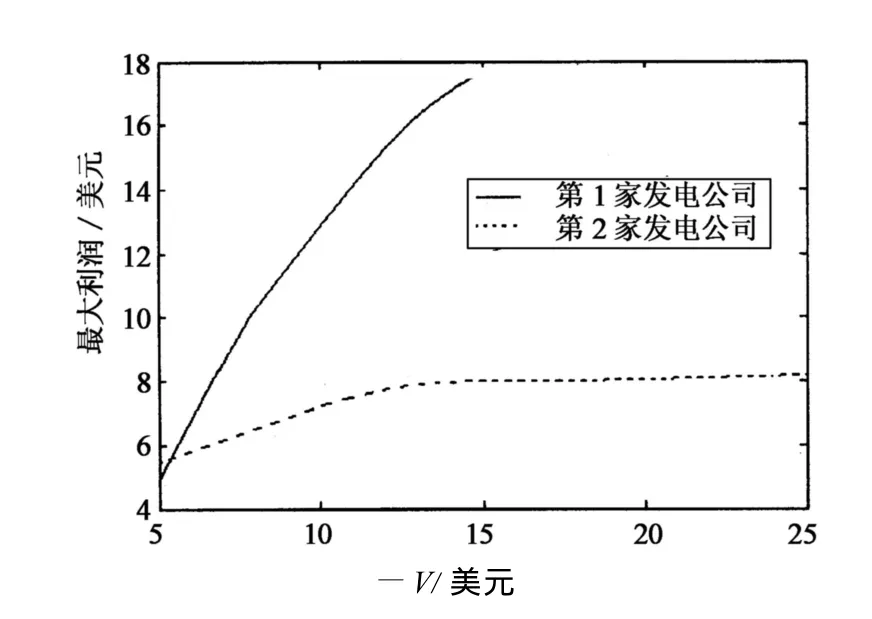
圖2 4節點2發電機系統效益前沿圖Fig.2 The maximum profit trend graph in different risk factor V

4.2 9節點3發電機系統中不同V下的效益

為了進一步測試該模型,采用IEEE 9-bus系統進行模擬求解.圖3為9節點3發電機系統的結構圖,其中1,2,3節點各有一個發電機,其余的為負荷節點.表4為線路參數表,表5是發電商技術與經濟參數表,表6是ISO負荷需求參數表.

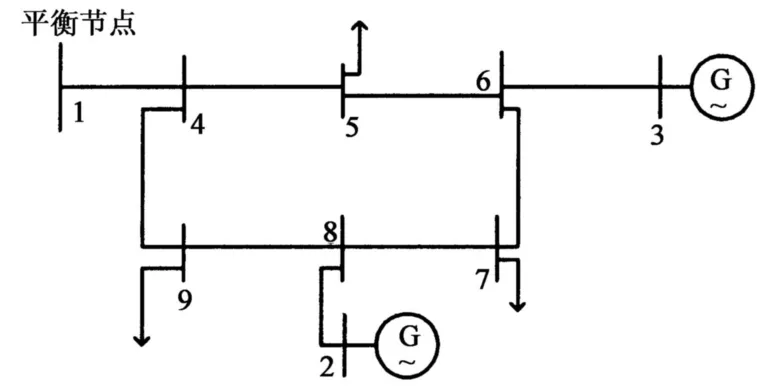
圖3 IEEE9節點系統圖Fig.3 9node 3 generator structure chart

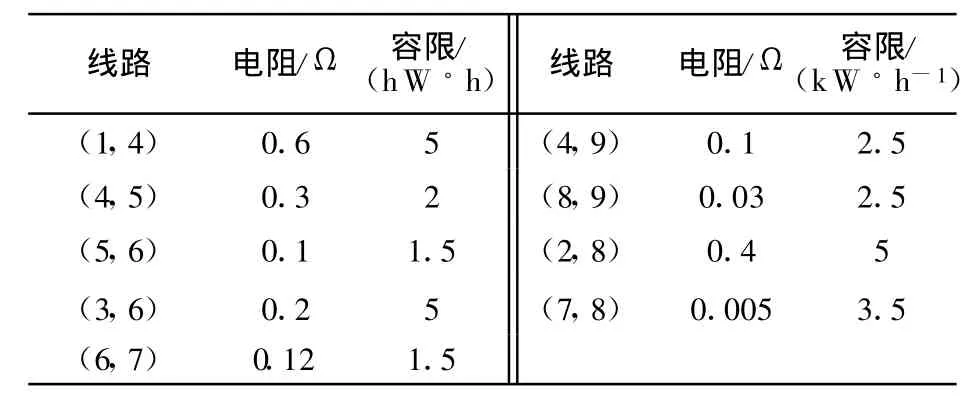
表4 線路參數Tab.4 Line parameters

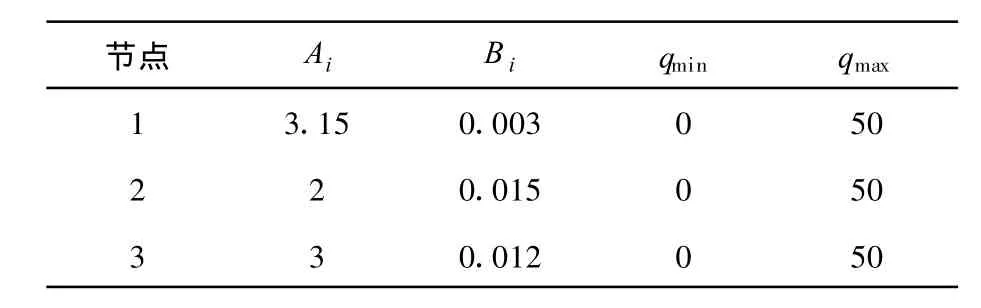
表5 發電機的技術和經濟參數表Tab.5 Generating technical and economic parameters

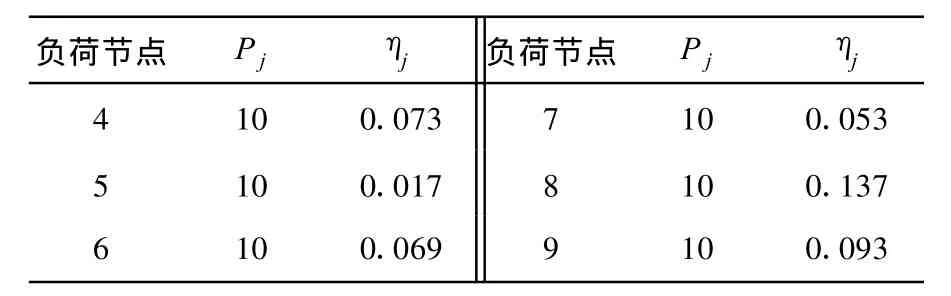
表6 負荷節點參數表Tab.6 Load node parameter

表7,表8和表9分別為IEEE9節點系統中發電商1,2,3在給定不同的V時所求得的最優投標系數、市場清除價R以及利潤.從計算結果可以看出:隨著V的降低,最優投標系數a2,b2,節點電價和利潤變化同4節點2機系統變化相同,電量隨投標系數變大而增加.從圖4可以看出利潤變化與4節點2發電機系統變化相同,增長到一定值以后不再隨V的變化而變化趨于平衡.

表7 發電商1在不同V下的最優投標系數以及結果Tab.7 The 1st generation company's result for a given different V

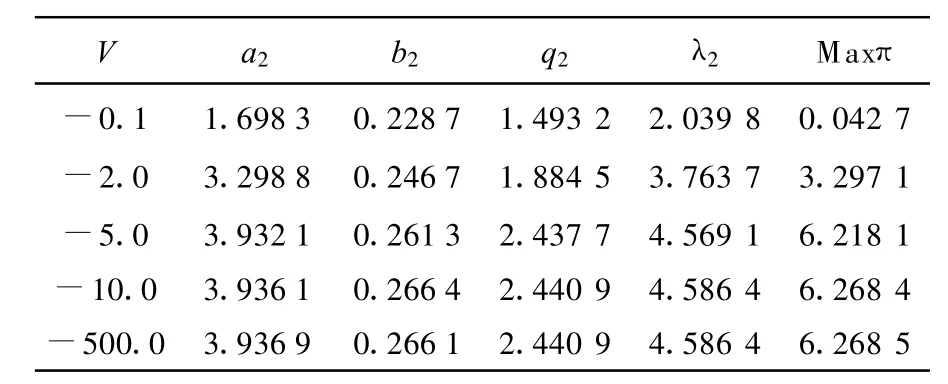
表8 發電商2在不同V下的最優投標系數以及結果Tab.8 The 2st generation company's result for a given different V

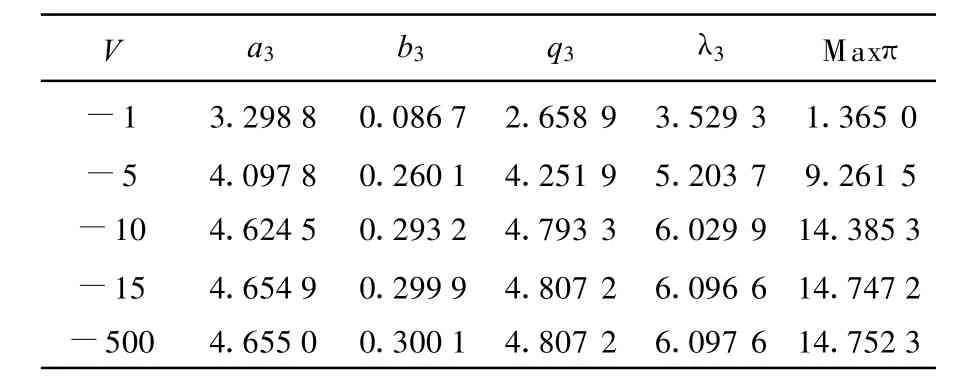
表9 發電商3在不同V下的最優投標系數及結果Tab.9 The 3st generation company's result for a given different V

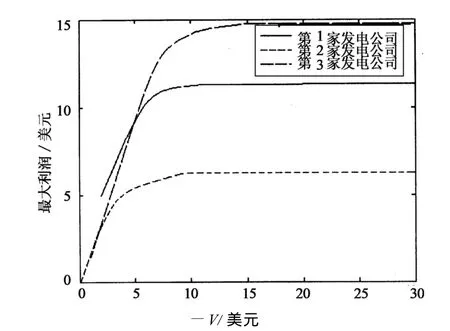
圖4 9節點3發電機系統效益前言圖Fig.4 The maximum profit trend graph in different risk factor V

5 結 論

本文在兼顧利潤最大和風險最小這兩個沖突目標情況下,構造了一種新的發電商最優投標策略優化模型,提出了基于Monte Carlo仿真和粒子群優化算法2種求解方法,通過數值實驗得出了以下結論:

1)風險因子V越小,投標系數隨之增大,投標相應增高.

2)風險越大,利潤越高.但是并不是無限制的提高,當V達到一定程度時,利潤就不再增長達到平衡,趨于一個相對穩定的數值.

3)由于本文模型設置f(x,y)為利潤函數的相反數,所以VaR,CVaR為一個負數,那么-CVaR值一般都小于-VaR值.雖然VaR,CVaR都是測量下偏風險,但VaR將注意力集中在一定置信度下的分位點上,而該分位點下面的情況則完全被忽略了,它使發電商忽略了某些極端的情況,而這些情況恰恰是發電商風險管理所必須關注的.而CVaR考慮了最壞情況中的所有情況,它比VaR值更準確地度量了發電商的風險.

4)PSO算法在求解類似該復雜約束非線性的投標模型問題中具有簡單易行、能求出全局最優解和快速收斂的優點,并且與初始點選擇無關.

[1] 余志森,程瑜,黃鶯.基于成本的電力供應商報價策略研究[J].華北電力技術,2008,38(4):1-4.YU Zhi-sen,CHENG Yu,HUANG Ying.Bidding strategies of demand-side based on cost analysis[J].North China Electric Power,2008,38(4):1-4.(In Chinese)

[2] MARKOWITZ H.Po rtfolio selection[J].Journal of Finance,1952,3(7):77-91.

[3] ALEXANDER G J,BAPTISTA A M.Economic implications of using a mean-VaR model for portfolio selection:a comparison with mean-variance analysis[J].Journal of Economic Dynamics and Control,2002,26:1159-1193.

[4] ROCKAFELLAR R T,URYASEV S.Optimization of conditional value-at-risk[J].The Journal of Risk,2000,2(3):21-41.

[5] 廖菁,江輝,彭建春,等.基于VaR和CVaR風險度量的發電商競價策略[J].繼電器,2007,35(11):31-36.LIAO Jing,JIANG Hui,PENG Jian-chun,et al.Risk assessment on bidding strategy of power generation companies based on VaR and CVaR method[J].Relay,2007,35(11):31-36.(In Chinese)

[6] HANSEN P,JAUM ARD,SAVARD G.Newbranch-andbound rules for linear bi-level programming[J].SIAM Journal on Science and Statistical Computing,1992,13(5):1194-1217.

[7] SAVARD G,GAUVINJ.The steepest descent direction for the nonlinear bi-level programming problem[J].Operations Research Letters,1994,15(5):265-273.

[8] BA RD J F.An efficient point algorithm for a linear two-stage optimization problem[J].Operations Research Letters,1983,31(4):670-684.

[9] M ATHIEU R,PIT TARD L,ANANDA LINGAM G.Genetic algorithm based approach to bilevel linear programming[J].Operations Research Letters,1994,28(1):1-21.

[10]ODVGUWA V,ROY R.Bi-level optimization using genetic algorithm[C]//Proceeding s of IEEE International Conference on Artificial Intelligence System,Divnomorskoe(Russia):2002:322-327.

[11]HOBBS B F,METZLER C B,PANG J S.Strategic gaming analysis fo r electric power systems[J].An MPEC Approach IEEE Trans on Power Systems,2000,15(2):638-645.

[12]馬超群,侯志儉,蔣傳文,等.基于粒子群算法求解電力市場發電商最優供給函數模型[J].電力系統自動化,2006,30(2):45-47.M A Chao-chun,HOU Zhi-jian,JIANG Chuan-wen,et al.PSO algorithm based optimal supply function model for power producer[J].Automation of Electric Power Systems,2006,30(2):45-47.(In Chinese)

[13]馬新順,文福拴,劉建新,等.計及輸電容量約束的發電公司最優報價策略[J].電力系統自動化,2005,29(10):6-10.M A Xin-shun,WEN Fu-shuan,LIU Jian-xin,et al.Development of optimal bidding strategies for generation companies considering transmission capacity constraints[J].Automation of Electric Power Sy stems,2005,29(10):6-10.(In Chinese)

[14]馬新順,文福拴,倪以信,等.計及風險并考慮差價合約的發電公司最優投標策略[J].電力系統自動化,2003,30(22):45-49.M A Xin-shun,WEN Fu-shuan,NI Yi-xin,et al.Development of risk-constrained optimal bidding straegies for generation companies in electricity markets with cantract for difference[J].Automation of Electric Power Systems,2003,30(22):45-49.(In Chinese)

[15]史忠植.高級人工智能[M].2版.北京:科學出版社,2006:47-50.SHI Zhong-zhi.Advanced artificial intelligence[M].The Second Edition.Beijing:Science Press,2006:47-50.(In Chinese)