單星多普勒變化率無源定位精度分析*

曹東波,張 敏,姜文利

(國防科技大學電子科學與工程學院,湖南長沙 410073)

0 引言

單星無源定位作為一種空間電子偵察技術手段,具有成本低、系統簡單、研發周期短等優點。但現有的單星測角定位系統,一般利用基線干涉儀獲取目標方位信息,對衛星的載荷、側向通道的相位一致性以及星載平臺的姿態控制和測量精度要求較高,定位精度不高。

利用多普勒頻率變化率作為測量量進行無源定位,是一種快速、高精度的單站無源定位新技術。它僅利用衛星在不同位置對同一個輻射源測量得到的多普勒變化率實現定位,對衛星姿態測控和通道特性無特殊要求,是一種低成本、低載荷、低功率需求的單星無源偵察定位系統,易于工程實現。研究表明,利用測量多普勒變化率實現無源定位的定位精度取決于多普勒變化率測量精度、載波頻率測量精度、高程假設誤差、衛星星歷誤差等因素。本文在簡要介紹基于多普勒變化率的單星無源定位原理的基礎之上,推導了參數測量精度與定位精度之間的關系,仿真分析了不同測量精度條件下定位誤差的分布情況。

1 定位原理

地面輻射源在工作過程中,必然有信號輻射到太空,高速運動的低軌電子偵察衛星從其所在區域上空通過時,該衛星上的天線接收機即可接收到地面輻射源的信號。考慮到衛星與輻射源之間存在相對運動,在衛星上接收到的信號將受到多普勒效應的影響,通過數字信號處理和數據處理即可獲得信號多普勒變化率信息。由于不同時刻多普勒變化率與目標位置具有對應關系,結合輻射源位于地球表面這一先驗信息的約束,即可多次測量解算出輻射源的位置。

假設如圖1所示,在地心直角坐標系中,設衛星位置ro=[xo,yo,zo]T,衛星速度為vo=[vox,voy,voz]T,衛星加速度為a o=[aox,aoy,aoz]T。地面固定輻射源的坐標為r T=[x,y,z]T,輻射源速度為v T=0,輻射源加速度為a T=0,載波頻率為f0,載波波長為λ。

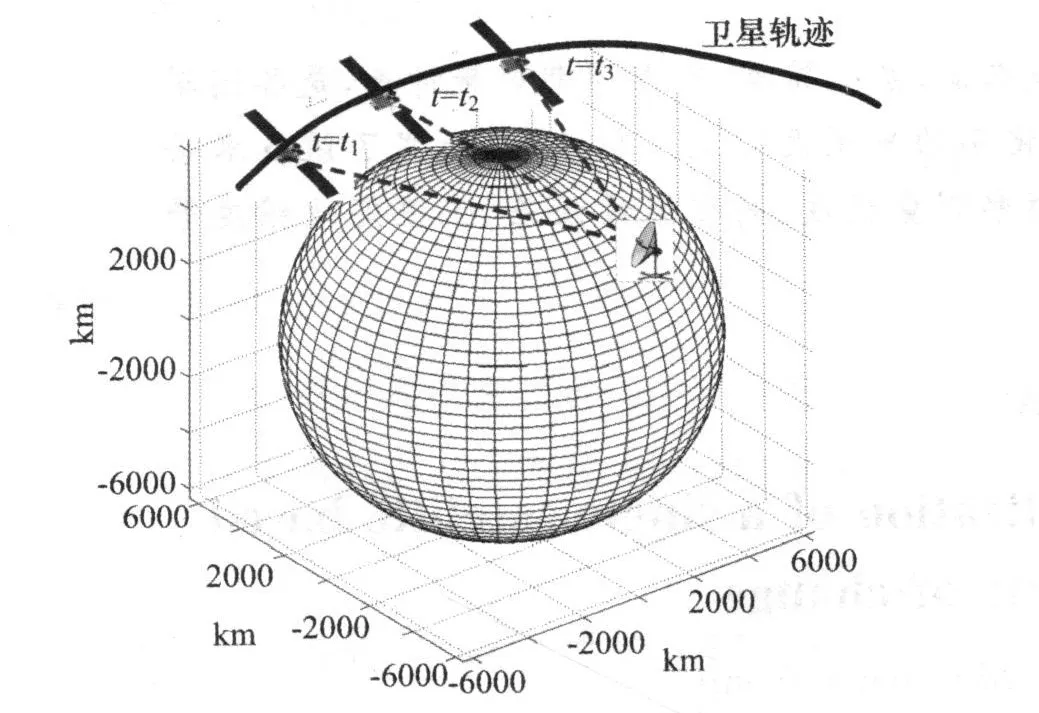
圖1 單星單通道定位模型示意圖

在不考慮相對論效應下,衛星接收機接收到的信號中包含了相對徑向速度調制的多普勒頻率分量,即:

式中,c為電磁波在介質中的傳播速度,﹒r為目標與衛星的徑向速度。

式中,r=r o-r T為目標與衛星的相對運動位置矢量,v=v o-v T為目標與衛星的相對運動速度矢量,r=((xo-x)2+(yo-y)2+(zo-z)2)1/2為目標與衛星的距離。

式(1)對時間求導得到多普勒變化率為:

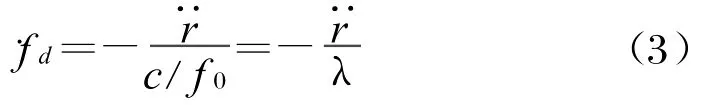
式(2)對時間求導得到目標與衛星的徑向加速度為:

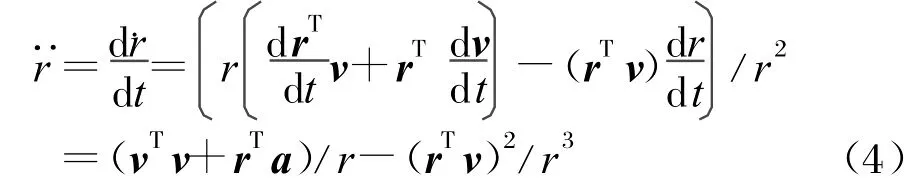
式中,a=d v/d t=a o-a T為目標與衛星的相對運動加速度矢量。

將式(4)代入式(3)得多普勒變化率為:

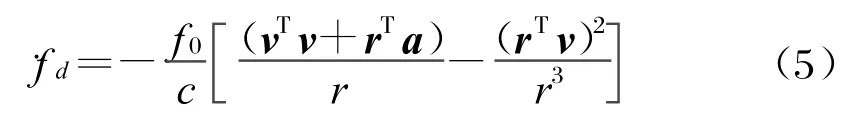
對地面靜止輻射源,衛星在飛過目標上空的在t1～tN時刻,接收機測量得到N個觀測值:

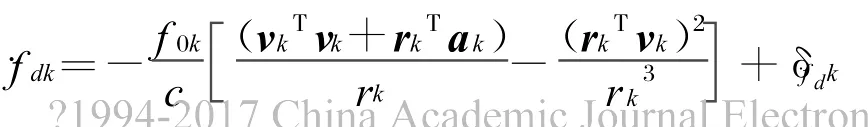
人們通常習慣于采用地球大地坐標系表示輻射源的位置。本文采用WGS-84地球模型,目標位置坐標用地球大地坐標系中經緯高(L,B,H)表示,它和地心直角坐標系有如下的轉換關系[1]:

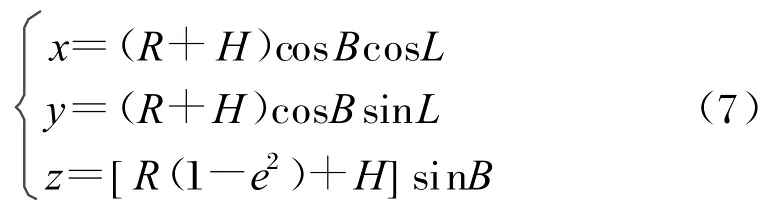
式中,R=a(1-e2sin2B)-1/2為地卯酉圈曲率半徑,a=6378.136km為地球的長半軸,e=0.081819190842552為第一偏心率。通過(7)式,目標位置坐標(x,y,z)被限制在地球的球面上,從而也構成了一個定位方程。

2 定位計算方法

通過(6)及(7)聯立,可求解出目標位置。在零高程假設情況下,采用在經緯度上進行網格搜索計算的方法來快速確定目標輻射源位置[2]。該算法無需初始值,也不需要對協方差陣求逆,算法過程如下:

1)根據多個時刻觀測器位置的中心點,計算觀測器軌跡在地面投影中心位置——中心星下點的位置。

2)以觀測器載體在地面的中心星下點為中心,在觀測器載體可能的地球球面探測范圍經緯度[±L m ax,±B max]內,均勻劃分M×M個網格點,其中L max和B max為目標最大可能的經度、緯度。

3)計算網格劃分線。將觀測器軌跡在地面投影的第一點X 1和最后一點XN連接成一條直線將步驟2)的M×M個網格點劃分為兩部分,分為直線左下部分的網格點和直線右上部分的網格點。

4)分別計算每一個網格點的代價函數。對于每一個網格點的經緯度,假定其海拔高度為h,計算其對應在地心固定坐標系下的三維位置(x,y,z),如果目標位于該點,則可根據星歷推算得到在任意tk時刻的理論頻率變化率值﹒fd(tk),再結合實際測量得到的頻率變化率(t),k=1,…,N,計算該點的代價函數:k

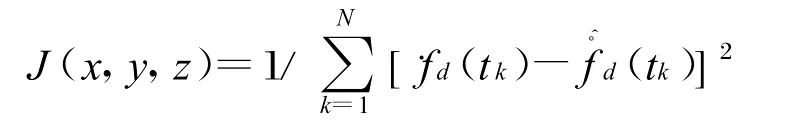
5)分別搜索右上部分網格點和左下部分網格點的代價函數J(x,y,z)峰值點,找到其對應的網格點坐標位置。

由于等多普勒頻率變化率定位曲面的對稱性,與地球相交于兩點,得到兩個關于星下點航跡對稱的定位點,因此存在著定位模糊問題,可利用其它信息剔除虛假信息得到唯一的目標位置。進行網格搜索時,網格點數M越大,估計越接近最小均方估計。當M較大時,為減小運算量,還可考慮采用多級搜索的辦法。

3 定位誤差的計算方法

從式(6)中可以看到,影響地面輻射源目標定位精度的因素主要包括:多普勒變化率測量誤差、載頻測量誤差、衛星星歷誤差。當采用在經緯度上進行網格搜索計算方法求解輻射源位置時,定位精度還受到高程假設誤差的影響。下面對定位誤差進行分析:

由式(7)可得[3]:

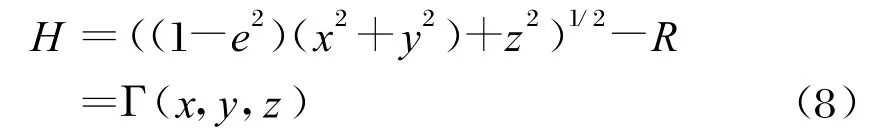
求全微分,得:

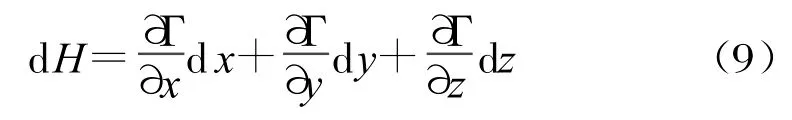
對式(6)求全微分,得:

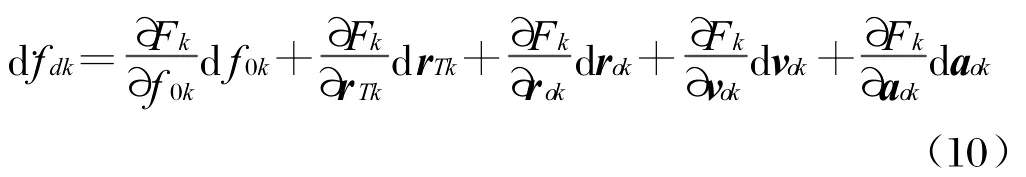
合并式(9)、(10),并寫成矩陣形式為:

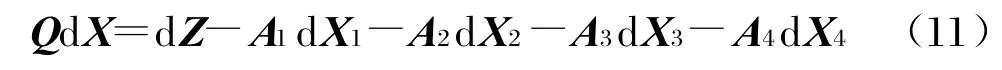
假設各測量誤差及定軌誤差不相關,RdZ為多普勒變化率與高程假設協方差陣,R d X1為載頻測量協方差陣,R d X2為衛星位置協方差陣,R d X3為衛星速度協方差陣,R d X4為衛星加速度協方差陣,則定位誤差的協方差矩陣為:

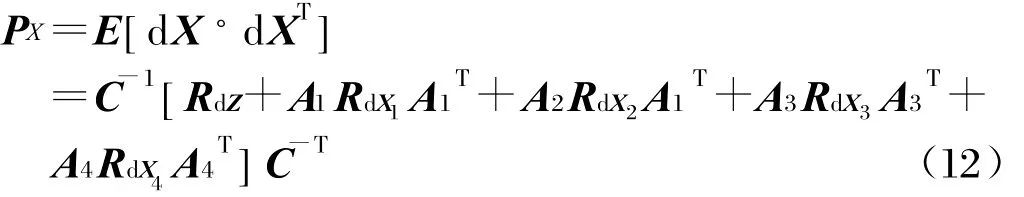
式中,C-1=(QTQ)-1QT。

衛星等航天器的運動滿足一定的軌道約束條件,衛星的加速度由其位置、速度矢量即可確定[4]。為便于分析,這里僅在二體問題下討論,此時衛星的加速度由其位置矢量即可確定。在二體問題下,根據萬有引力定律可知[5]:

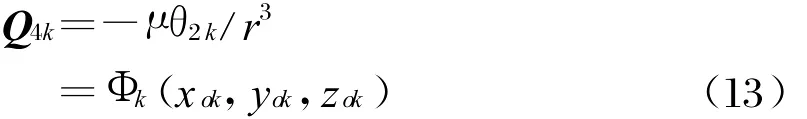
式中,μ=3.986004415e14m3/s2為地球引力常數,Φk=[φxk(xok,yok,zok),φyk(xok,yok,zok),φzk(xok,yok,zok)]T。

對上式求其全微分得:

若衛星位置定軌精度為10m數量級,利用式(12)得到的衛星加速度的精度為1e-5ms-2數量級。從后文的仿真也可以看到,此數量級的加速度引起的定位誤差很小。故式(10)可簡化為:

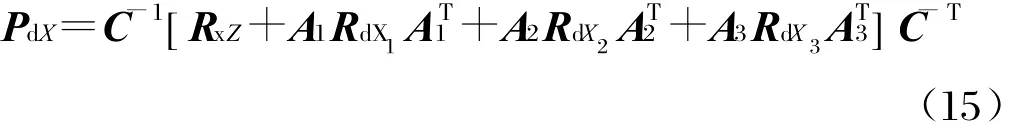
用水平分量來衡量定位精度時,將式(15)經如下變換:

根據式(16)計算定位面上每點(L,B)的定位水平誤差,可以得到理論誤差的GDOP(Geometric Dilution of Precision)[7]分布為:

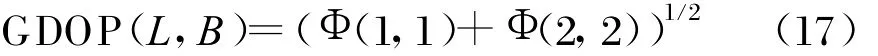
4 仿真結果及分析

在無特別說明情況下,仿真選取的基本參數如下:載頻變化率測量精度σ1為1H z/s,高程假設精度σ2為0.1km,載頻測量精度σ3為1MH z,衛星位置精度σ4為0.030km,衛星速度精度σ5為0.001km/s。在測量定位參數期間,假設輻射源的載頻沒有發生捷變,且每隔10s進行一次測量。

利用STK(Satellite Tool Kit)仿真軟件獲取衛星運行的星歷數據[8]。假設衛星高度400km;輻射源載頻為1.3GHz;雷達轉速6r/min,測量起始時刻衛星在地心直角坐標系中的衛星的位置為(-3173.3291,4921.6562,3412.9999)km,初始速度為(-0.7948,4.035,-6.5580)km/s,初始加速度為(0.0046,-0.0062,-0.0044)km/s2。圖中*代表衛星星下點軌跡。

圖2為不同測量精度條件下輻射源水平定位精度。由圖可知,單星僅測多普勒變化率無源定位的誤差是關于衛星星下點軌跡成對稱分布的。通過圖(a)與(c)可知多普勒變化率測量精度對系統定位精度影響最大,要實現快速高精度單星無源定位,多普勒變化率的測量精度最好達到1Hz量級。通過圖(a)與(b)可以看出,高程假設誤差會引入一定的定位誤差,特別是在星下點附近產生的誤差較大。通過圖(a)與圖(d)可以看出載頻測量對定位誤差分布影響不大。從圖(e)、(f)中可以看出,衛星星歷誤差對定位誤差分布影響很小,且隨著衛星定軌技術的發展,衛星位置定軌精度可達到10m量級,速度定軌精度可達到1m量級,甚至更小,因此星歷誤差對單星多普勒變化率定位精度的影響幾乎可以忽略。

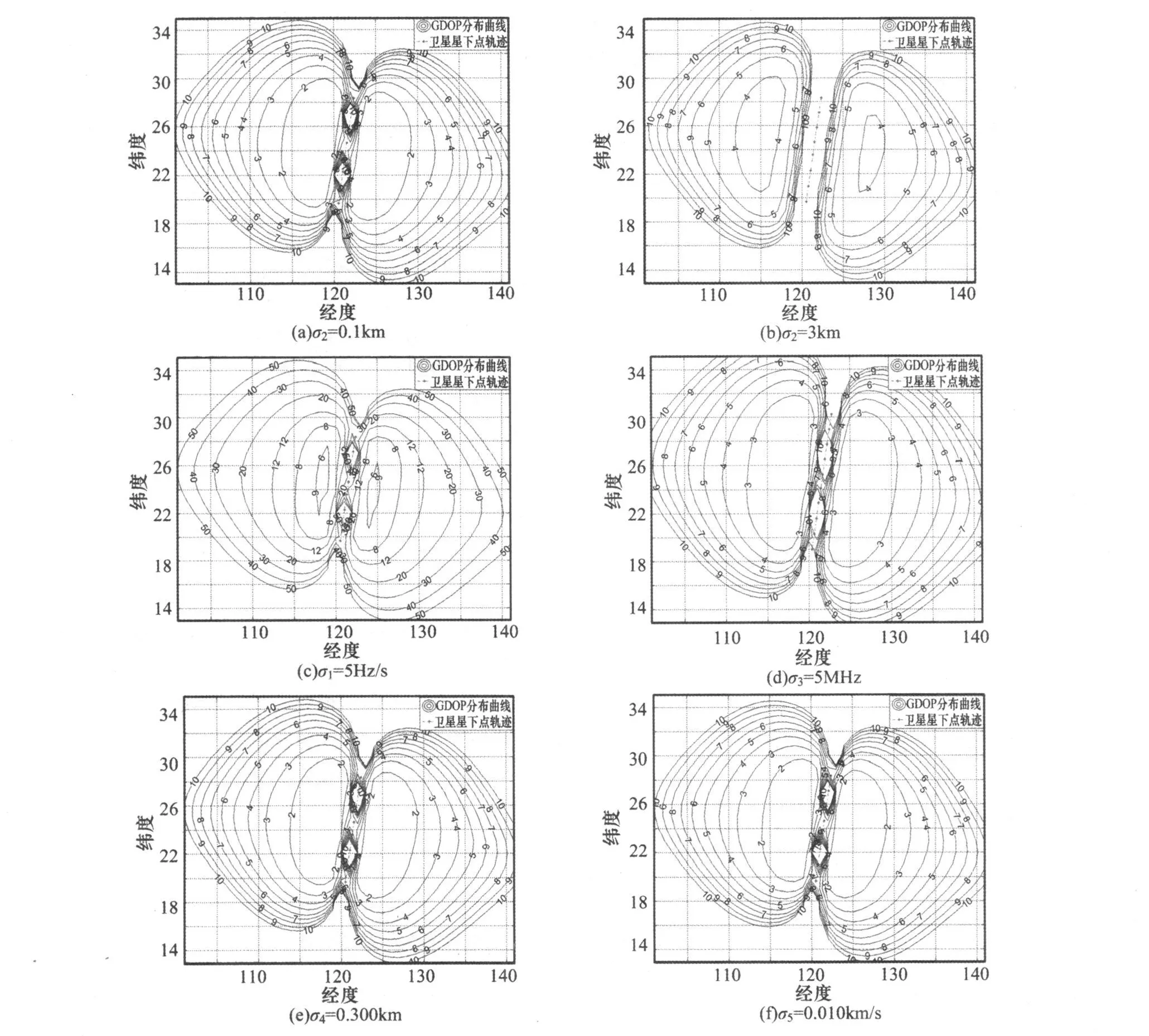
圖2 定位精度仿真結果

5 結束語

單星測多普勒變化率無源定位方法具有有效載荷小、研發周期短、對衛星姿態無特殊要求等特點。本文重點分析了采用各種測量精度對定位精度的影響,通過仿真發現,在現有的測量條件及測量精度下,衛星星歷誤差、高程假設誤差、頻率測量精度對定位誤差分布的影響較小;多普勒變化率的測量精度對定位誤差分布的影響最大,是實現快速高精度單星無源定位的關鍵因素。本文的工作對單星定位系統的設計和工程應用具有一定的參考價值。■

[1] 邊少鋒,柴洪洲,金際航.大地坐標系與大地基準[M].北京:國防工業出版社,2005.

[2] 張敏,馮道旺,郭福成.基于多普勒變化率的單星無源定位[J].航天電子對抗,2009,25(5):11-13.

[3] 林雪原,劉建業.北斗雙星定位系統改進及其算法研究[J].空間科學學報,2003,23(2):149-154.

[4] 劉利生,吳斌,楊萍.航天器精確定軌與自校準技術[M].北京:國防工業出版社,2005.

[5] 張守信.外彈道測量與衛星軌道測量基礎[M].北京:國防工業出版社,1992.

[6] 鐘單星,鄧新蒲,周一宇.基于WGS-84橢球模型的衛星測時差定位精度分析[J].電子對抗技術,2002,17(5):18-21.

[7] 孫仲康,郭福成,馮道旺,等.單站無源定位跟蹤技術[M].北京:國防工業出版社,2008.

[8] 楊穎,王琦.STK在計算機仿真中的應用[M].北京:國防工業出版社,2005.