基于時頻分布的電子偵察信道參數(shù)估計方法

江 莉,董 惠,李 林,劉 利

(1.西安建筑科技大學信息與控制工程學院,陜西西安 710055;2.西安電子科技大學電子工程學院,陜西西安 710071)

0 引言

在通信、雷達、聲納等電子偵察與對抗方面,截獲的信號總是伴隨著多徑干擾。通過ESM、ELINT等電子偵察設備截獲的信號,對信道參數(shù)進行有效的估計,可以提高信號檢測概率,提高信號參數(shù)估計精度,在電子偵察與對抗方面具有非常重要的應用價值。多徑信道參數(shù)估計實際上是一個盲反卷積過程,文獻[1～2]針對重疊的雷達多徑信號,通過天線陣列模型進行多徑參數(shù)估計,此時需要滿足天線陣列數(shù)大于多徑信道個數(shù)的條件。對于單通道偵察接收設備而言,僅有一個觀測脈沖序列,信道一般具有時變性,因此理論上單個多徑信號的盲反卷積的解是不存在的。文獻[3]針對多徑信道中的信號調制識別問題,采用子空間方法估計信道參數(shù),該方法對噪聲敏感,適用范圍有限。文獻[4]采用循環(huán)自相關方法通過構造降階函數(shù)對多徑信號進行檢測與參數(shù)估計,但該方法僅適用于LFM信號。本文針對單通道電子偵察系統(tǒng),提出了一種基于時頻分布的信道參數(shù)盲估計方法。該方法快速簡單,參數(shù)估計準確,分辨率高。

1 理論基礎

1.1 信道模型

假設發(fā)射信號為s(t),經(jīng)過多徑信道傳輸,最后接收到的信號可表示為:

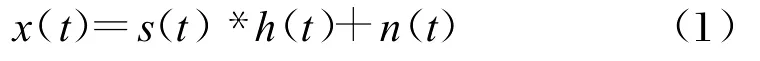
式中,h(t)為傳播信道的沖激響應,n(t)為窄帶高斯白噪聲。

因為各徑時延和幅度因子均未知,即使不考慮噪聲,數(shù)學上(1)式的解不唯一。假設源信號s(t)為:

式中,a(t)和φ(t)分別是瞬時幅度和相位。

由多徑信道模型可知,每一多徑信號分量與源信號s(t)具有相同的瞬時頻率結構,其差別僅在于時間延遲。因此,可通過時頻域的匹配濾波完成多徑參數(shù)估計。通過Moyal公式[5],可以將任意的時頻互分布形式與其時域信號相聯(lián)系,

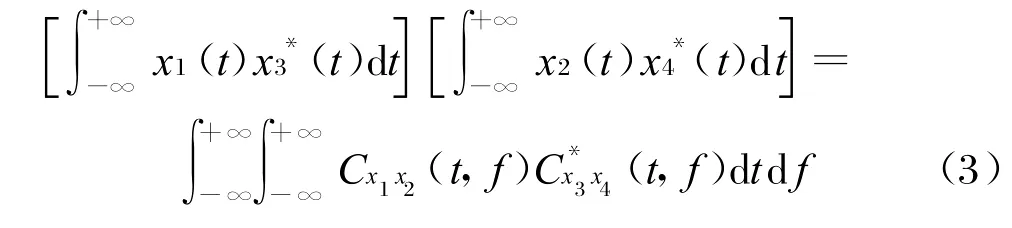
令x(t)=x1(t)=x2(t),s(t-τ)=x3(t)=x4(t),可得:

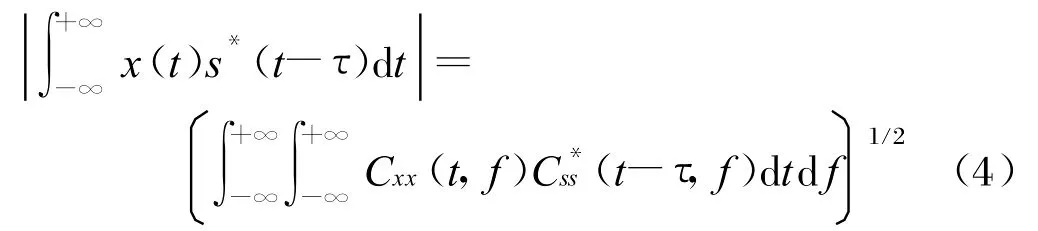
因此,時域匹配濾波同樣可以在時頻域進行。

1.2 時頻分布

短時傅里葉變換是最基本的線性時頻表示方法,可定義為:

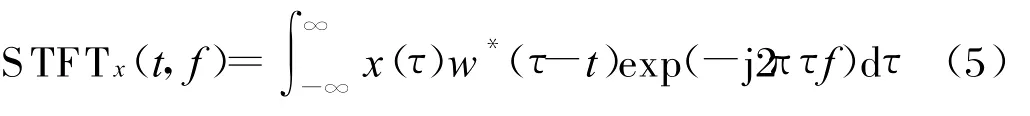
式中,w(t)是窗函數(shù)。根據(jù)不確定原理,時間窗寬度和頻率窗的寬度彼此成反比。若時間窗取得較長,則可得到較好的頻率位置,但是時間分辨率卻比較差。因此,好的時間分辨率必然意味著差的頻率分辨率。相反地,好的頻率分辨率意味著差的時間分辨率[6]。

具有雙線性特性的時頻分布(稱為Cohen類)可以用統(tǒng)一的形式表示為:

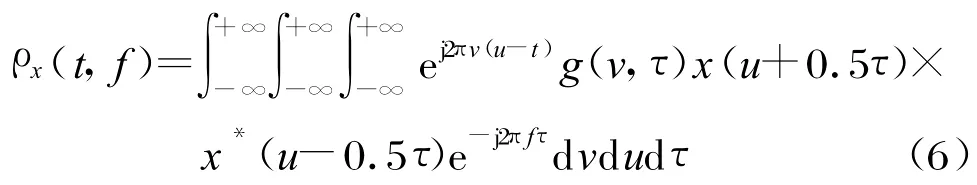
式中,g(v,τ)是加權函數(shù),稱為核函數(shù)。特別地,當g(v,τ)=1,即ψ(t,ω)=2πδ(t)δ(ω),可得常用的Wigner-Ville分布。WVD具有很多優(yōu)良的性質,在所有的時頻技術中具有幾乎最優(yōu)的時頻分辨率,但是其主要缺點是會產(chǎn)生交叉項干擾。

時頻分布與模糊函數(shù)密切相關,模糊函數(shù)A(v,τ)可定義為[7]:

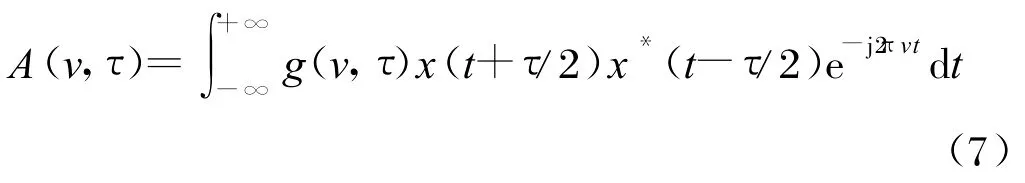
對傳統(tǒng)的模糊函數(shù)用核函數(shù)進行平滑,然后再進行二維傅里葉變換,即可得到Cohen類二次時頻分布的統(tǒng)一形式。一個信號的Cohen類時頻分布實際上是一個時頻域上的二維函數(shù)對該信號WVD平滑的結果,通過適當?shù)暮撕瘮?shù)選擇,可以減小或去除多分量信號的交叉項干擾,但交叉項的抑制會導致時頻分辨率下降。

2 基于時頻分布的多徑信道估計

2.1 多分量信號的時頻分布

多徑信號也可看作一類特殊的多分量信號。為了有效地在時頻域進行匹配濾波,首先對WVD的自身項和交叉項在時頻平面的分布特點進行研究。簡單起見,假設分析信號x(t)包含兩個信號分量s1(t)和s2(t)。

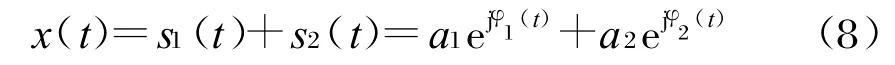
式中,φ1(t)和φ2(t)分別表示兩信號分量的瞬時相位。根據(jù)WVD的定義有:

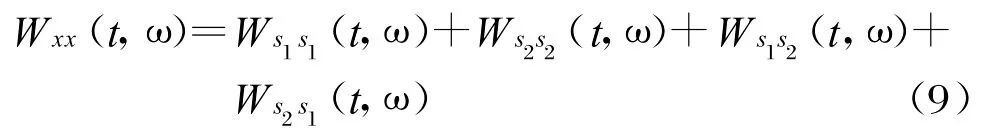
式中,前兩項為自身項,而后兩項是交叉項。交叉項由不同信號分量之間的相互作用造成,嚴重影響了信號時頻分布的分辨性能和解釋性。

對于式(9)的自身項Ws1s1(t,ω),將φ1(t)在t附近按照Tay lor級數(shù)展開可以得到:

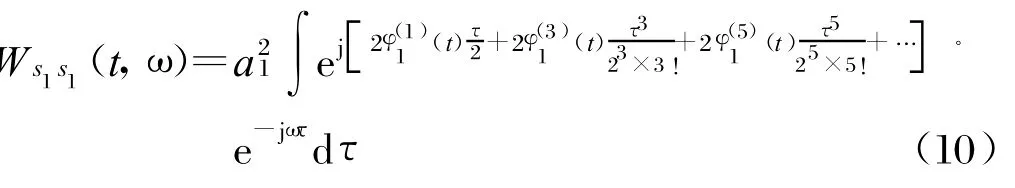
同理,交叉項Ws1s2(t,ω),將φ1(t)和φ2(t)分別按照Tay lor級數(shù)展開可以得到:

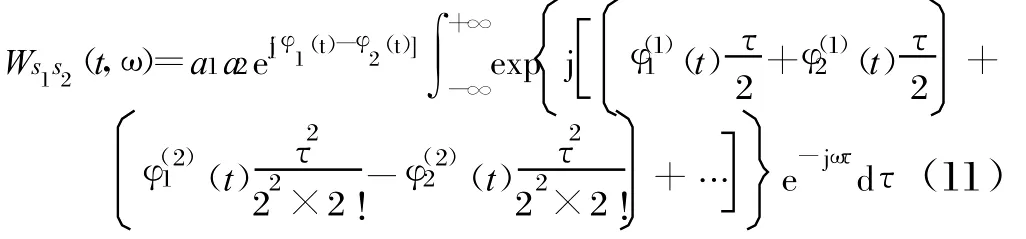
式(10)和式(11)中的Fourier變換求解較為復雜,這里僅做定性分析。以式(10)為例,其中的時域函數(shù)的導數(shù)可表示為:

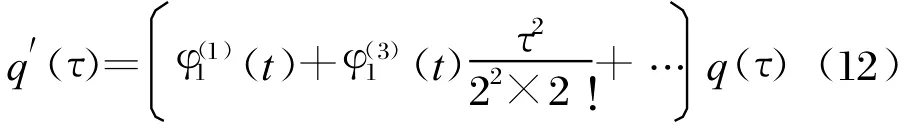
根據(jù)Fourier變換的時域和頻域微分的性質,可得:

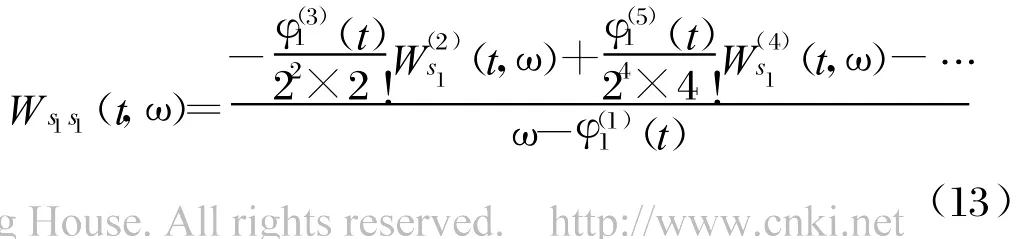
上式是一個高階齊次微分方程,其通解為一實函數(shù)。且Ws1 s1(t,ω)會在瞬時頻率ω=φ(11)(t)處出現(xiàn)峰值。同時由于相位中高次項的作用,會產(chǎn)生由信號自身帶來的交叉項。同理,式(11)中信號交叉項的WVD也可表示為一個高階齊次微分方程的解:

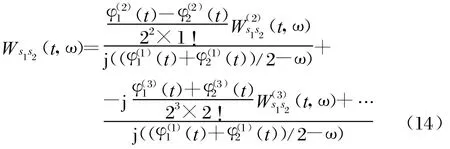
可以看出,信號交叉項的WVD一般為復函數(shù),其模值在ω=(φ′1(t)+φ′2(t))/2時具有峰值,同時由于相位中高次項的作用,會產(chǎn)生復雜的交叉項干擾。

特別地,如果信號相位的三階以上的導數(shù)為零,即LFM信號,則:

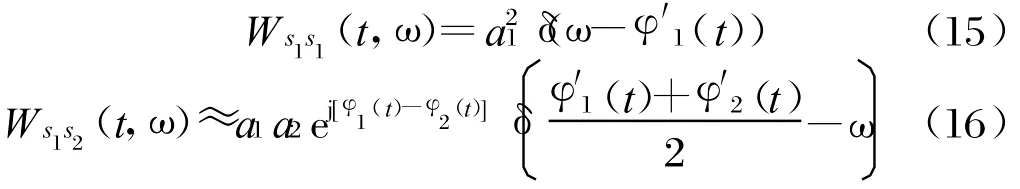
此時,自身項就是位于該信號瞬時頻率位置上的一個沖激函數(shù),表現(xiàn)出最佳的時頻聚集性。而兩個信號的交叉項在兩信號瞬時頻率的中心位置處出現(xiàn)沖激,在其他區(qū)域也有交叉項產(chǎn)生,并且離中心頻率越近,交叉項干擾越大。實際中,由于信號分量間能量的差異,交叉項的峰值有可能大于信號自身項。此時,交叉項的幅度隨時間振蕩,振蕩的瞬時頻率主要受兩信號瞬時相位差影響。

2.2 基于時頻分布多徑參數(shù)估計

通過以上分析可知,相比其他二次時頻分布,WVD形式最為簡單,具有最優(yōu)的時頻聚集性,但交叉項的干擾不可避免。對于線性調頻信號,假設信道沖激響應h(t)=a1δ(t)+a2δ(t-D 2),即僅包含一路多徑信號,經(jīng)推導可得:

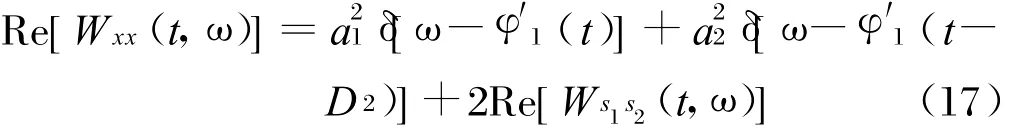
對于離散信號,并根據(jù)交叉項時頻分布振蕩的特點,信道參數(shù)可近似表示為:

式中,τ=1,2,…,N,N為信號長度。一般源信號s(t)的能量要大于其他多徑分量,因此可通過時頻圖中的峰值軌跡來估計源信號的瞬時頻率f(t)。

由交叉項引起的信道估計誤差可表示為:

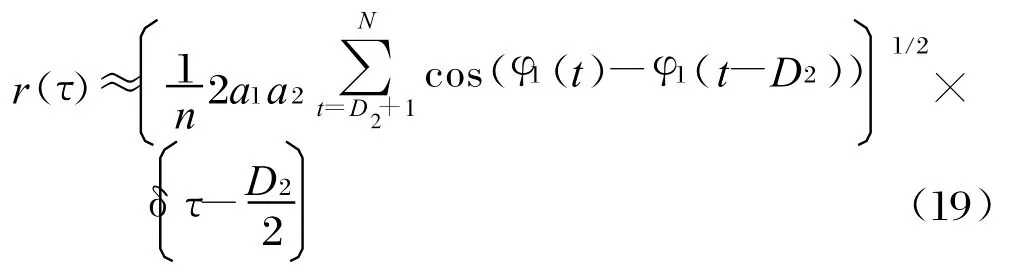
由此可證明,數(shù)據(jù)長度越長,r(τ)越小,信道參數(shù)估計精確越高。另外,信號的調頻斜率越大,即相位差(φ1(t)-φ1(t-D2))越大,r(τ)越小。

然而,實際中處理的信號總是長度有限,調制方式復雜,信號的WVD會產(chǎn)生由自身項帶來的交叉項干擾,且形式較為復雜。交叉項干擾將會產(chǎn)生錯誤的信道參數(shù)估計。可以采用平滑偽WVD,或其它Cohen類WVD抑制交叉項,但卻會大大降低信道參數(shù)估計的分辨率和精度。基于此,本文將短時傅里葉變換與WVD相結合,利用短時傅里葉變換良好的抑制交叉項性能,對WVD時頻圖進行濾波。在抑制交叉項干擾的同時,有效保留時頻圖的高分辨性能。算法流程如圖1所示。

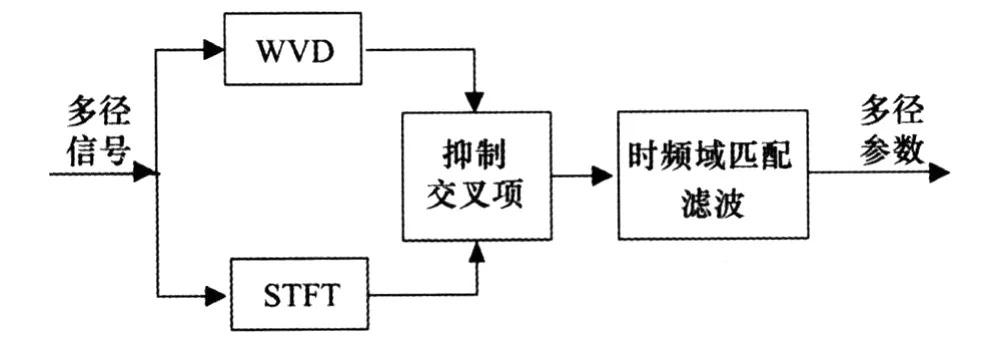
圖1 基于時頻分布的多徑信號參數(shù)估計

3 仿真實驗與結果分析

計算機仿真的多徑信號包含1個源信號和2個多徑分量。信道參數(shù)為:多徑時延D2=300、D3=500,幅度因子a2=0.4、a3=0.3。對于LFM信號,信噪比為5dB,結果如圖2所示。

圖2(a)是通過對Choi-William s分布[8]進行時頻域匹配濾波得到的多徑估計結果。可以看出,CWD有效地抑制了交叉項干擾,并在多徑時延處出現(xiàn)峰值。然而多徑濾波結果的分辨率較低。圖2(b)是直接采用WVD進行時頻域匹配濾波的結果,可以看出,該方法具有較高的分辨率。然而,由于噪聲和各種交叉項干擾影響,以及計算WVD時FFT長度的限制,匹配濾波的結果出現(xiàn)很多虛假的信道參數(shù)估計。

與上面兩種方法相比,圖2(c)是采用本文方法進行時頻域匹配,由多徑參數(shù)估計結果可以看出,該方法有效地抑制了各種干擾因素的影響,保留了對多徑幅度因子和時延估計的精度和分辨率。需要注意的是,利用短時傅里葉變換對WVD時頻圖進行濾波前,先要對短時傅里葉變換結果進行0/1二值化處理。二值化處理時采用的門限不能選擇過高,否則會導致多徑分量的時頻脊線丟失,而門限過低對估計結果的影響并不是很大。實驗中選取的歸一化后的二值化門限為0.25。

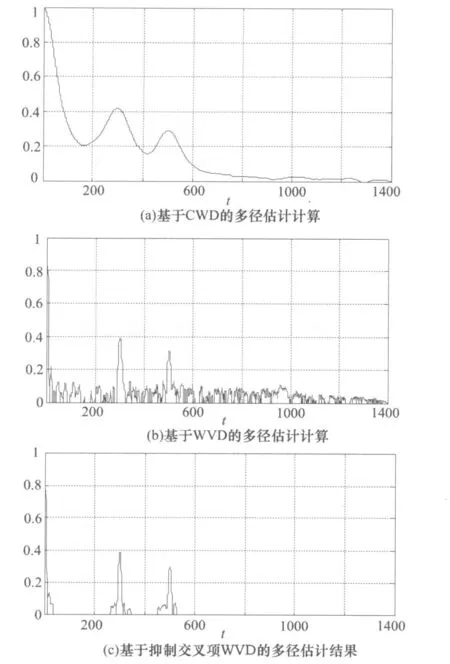
圖2 多徑LFM信號盲估計

圖3是在不同信噪比下,采用本文方法分別對第1多徑D2和第2多徑時延D3估計的絕對誤差。其中,LFM信號參數(shù)與上面實驗相同。除此之外還增加了4階頻率調制信號,多徑參數(shù)與LFM信號相同。圖中曲線是100次M onte-Carlo實驗的平均結果。可以看出,即使在較低信噪比下,采用本文方法對多徑LFM和四次頻率調制信號的時延估計誤差都比較小。當信噪比大于17dB時,時延估計誤差基本上可看作零,而此時對幅度因子a2和a3的估計的絕對誤差都在0.01以下。且對于多徑LFM信號的估計誤差要小于四次頻率調制信號,這與前面第2節(jié)中的分析結果一致。

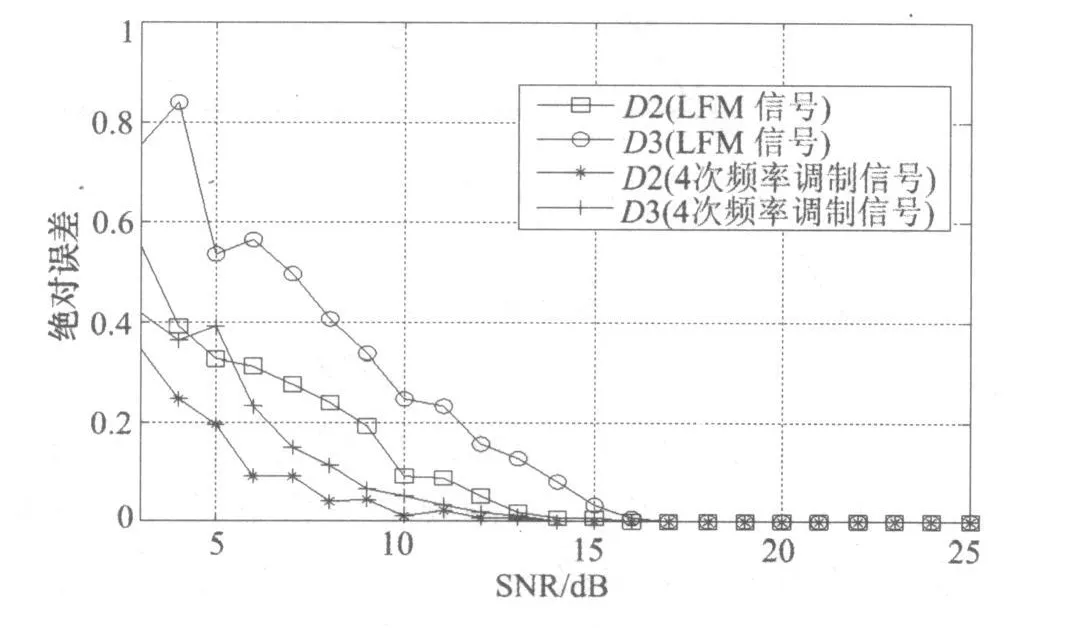
圖3 時延的估計性能

4 結束語

理論分析和計算機仿真實驗證明,本文提出的方法簡單、有效,且估計結果具有較高的分辨性能和估計精度。然而,源信號的瞬時頻率估計對算法性能影響較大,在輸入信噪比較低的情況下,信道估計性能將會受到較大的影響。另外實際中接收到的信號可能僅是發(fā)射信號的一部分,源信號和多徑分量信號會產(chǎn)生一定的失配,匹配濾波的性能也會受到較大的影響。此時應該引入其他的瞬時頻率估計方法,進一步抑制交叉項干擾。■

[1] Ayadi J,Zhan H,Faserotu J.Maximum likelihood time of arrival estimation for u ltrawideband signals[J].International symposium on Signal Processing and its app lication,2007(2):1-4.

[2] Swind lehurst A L,Gunther JH.Methods for blind equalization and resolution o f overlapping echoes of unknow n shape[J].IEEE Trans.on Signal Processing,1999,47(5):1245-1254.

[3] 王彬,葛臨東,徐立清.一種多徑信道中的調制識別算法[J].數(shù)據(jù)采集與處理,2007,22(4):440-446.

[4] 史建峰,王可人.基于循環(huán)相關變換的多徑LFM信號檢測與參數(shù)估計[J].電子與信息學報,2007,29(6):1377-1379.

[5] H law asch F.Regularity and unitarity of bilinear time-frequency signal rep resentations[J].IEEE Trans.on Information Theory,1992,38(1):82-94.

[6] Chen VC,H ao L.Time-frequency transforms for radar imaging and signal analysis[M].Boston,London:A rtech H ouse,2002.

[7] Barkat B,Boashash B.A high-resolution quadratic timefrequency distribution formu lticomponent signals analysis[J].IEEE Trans.on Signal Processing,2001,49(10):2232-2239.

[8] Sejdic E,Djurovic I,Jiang J.Time-frequency feature representation using energy concentration:An overview o f recent advances[J].Digital Signal Processing,2009,19(1):153-183.