基于遺傳退火算法的數字陣列稀疏布陣
代培龍,張仕元,肖文書
(南京電子技術研究所,江蘇南京 210039)
0 引言
為了提高雷達在復雜電磁環境中的使用性能,數字陣列雷達的研究已成為新的熱點。但是數字陣陣元數與系統的成本以及設備的復雜度成正比關系,同時天線的陣元數也影響處理速度[1],所以怎么設計天線陣的元數、單元間距、單元上電流的幅度與相位分布以獲得好的天線性能具有重要的意義。針對這一問題提出了很多方法:Skolnik采用密度錐削的方法[2],這種方法簡單,很容易應用于大型陣列的設計中,但它不能保證副瓣峰值電平被抑制到低于給定的電平。動態編程法是一種控制副瓣峰值電平的好方法,可以應用于大型陣列,但是極易陷入局部最小值。許多傳統的優化方法(例如Powell方法、共軛梯度法等)則不適合優化大量參數或離散參數。
近年來,遺傳算法和模擬退火算法等概率性全局優化算法得到了廣泛關注與應用[3-4],文獻[5~6]采用遺傳算法對線陣進行了優化,改善了陣列的副瓣電平,但是實際應用時遺傳算法極易陷入局部最優。本文在64個天線位置上隨機稀疏布陣32個天線單元、將天線單元位置,單元激勵作為自由度采用遺傳退火算法進行了全局優化,降低了副瓣電平,避免了遺傳算法陷入局部最優,提高了算法的優化時間性能,比遺傳算法有更快的收斂速度。
1 隨機稀疏布陣的數字陣列
數字陣列雷達接收和發射波束均以數字方式形成。其發射和接收由T/R組件來完成,以一個均勻排列的線陣為例來說明數字陣列的方向圖函數,如圖1所示。M陣元的均勻陣列天線,陣元間距為d,第m個天線單元的激勵電流為Im(m=0,1,2,…,M-1),各天線單元的方向圖函數為fm(θ),遠場目標方位角為θ,可將各發射信號看作平行發射,那么相鄰兩個天線單元發射信號的波程差為d sinθ,則所對應的相鄰兩個天線單元的的相位差為:
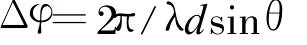
數字陣列由實時信號處理機產生每個天線單元的幅相控制字,對各T/R組件的信號產生器進行控制,產生一定頻率、相位和幅度的射頻加權信號。則經幅相加權后陣列的輸出方向圖函數為:
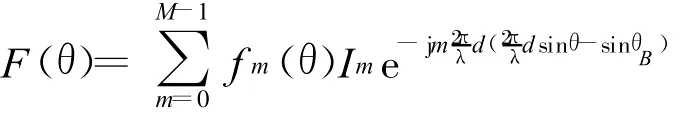
此時天線最大值指向為θB。
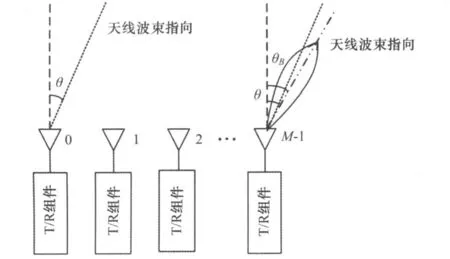
圖1 陣元數目為M的線陣示意圖
2 遺傳退火算法優化天線陣列原理
近年來,遺傳算法(GA)和模擬退火(SA)等概率性全局優化算法得到了廣泛關注與應用,但實際應用時常出現GA早熟收斂和SA搜索冗長的現象。而將兩者結合,SA的可控制收斂性避免出現早熟現象,GA并行化的抽樣過程可提高算法的優化時間性能。
遺傳退火的算法流程[7]如下:
1)隨機產生初始群體,計算初始溫度T
2)評價種群中每個個體的適應度
根據具體問題的優化目標構造適應度函數,使陣列方向圖符合某種給定的曲線形狀或者某個點或者區域落在規定的數值范圍內(如形成零陷、達到給定的副瓣電平)。本文以降低天線陣的旁瓣電平為優化目標,所以選擇最大峰值旁瓣比(RSLL)作為適應度函數,可定義為:
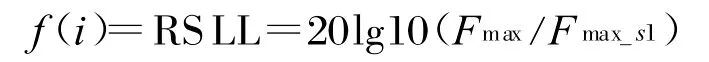
式中,F max是主瓣電平,F max_s1是最大旁瓣電平。
3)重復以下步驟,直至滿足收斂準則
a)從種群中隨機選取兩個個體Xi、Xj,以交叉概率P進行交叉操作,產生新的個體X′i、X′j,并計算適應度f(X′i)、f(X′j),如果m in{1,exp(-(f(X′i)-f(Xi))/T)}>random[0,1],則接受X′i為新個體;如果min{1,exp(-(f(X′j)-f(X j))/T)}>random[0,1],則接受X′j為新個體(此即METEOPOIS規則),random為[0,1]區間上的隨機數。
b)對種群中的每個個體Xi按變異概率Pm進行變異操作,產生新的個體X′i,同樣以METEOPOIS規則決定是否接受X′i。
c)更新溫度參數T=αT,這里0<α<1。
4)輸出結果
3 稀疏陣列優化的仿真結果
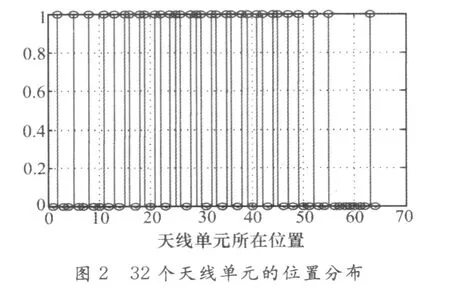
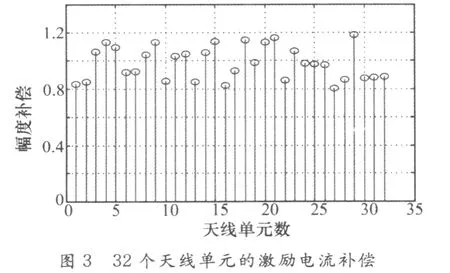
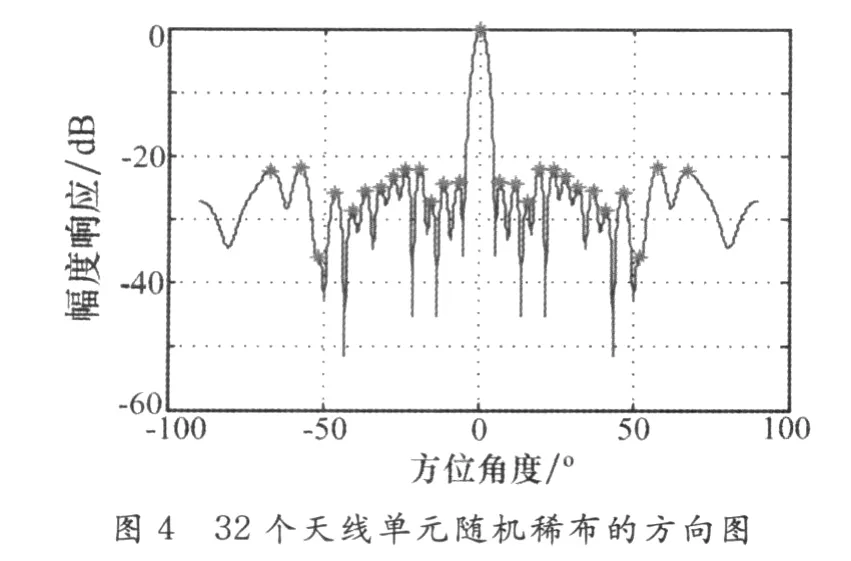
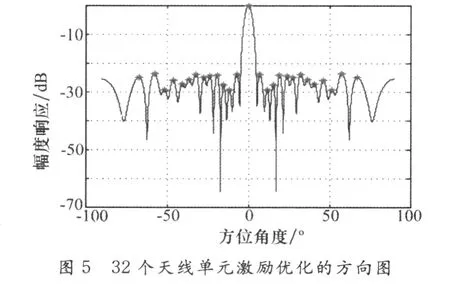
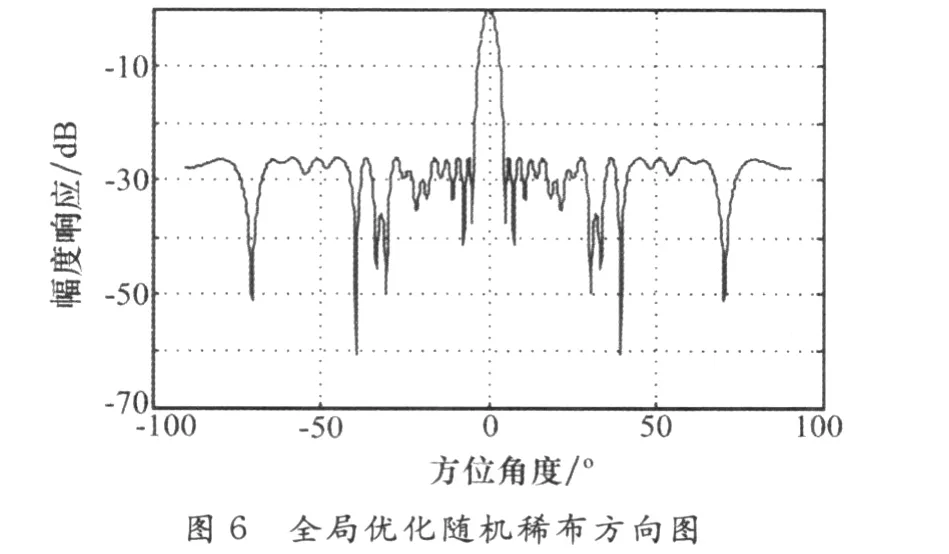
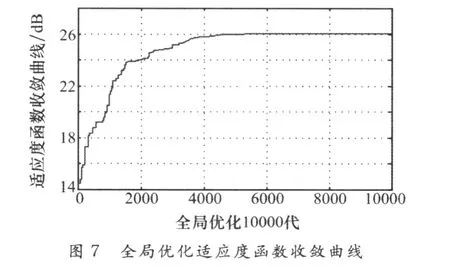
仿真中以降低最大相對旁瓣電平為最優化目標,采用全局遺傳退火算法和局部遺傳算法對陣元間距d為λ/4的32個天線單元、在64個位置進行了稀疏布陣,陣元位置和單元激勵采用二進制編碼,它們的基因都是由二進值符號集{0,1}所組成的。隨機產生單元位置和單元激勵的初始種群,種群規模為100,交叉概率為0.6,變異概率為0.01,先對天線單元位置編碼經過5000次迭代終止,再對單元激勵種群經過5000次迭代終止。局部優化得到的天線單元位置和幅度補償結果如圖2和圖3,在仿真中采用了文獻[8]中所采用的GA結合FFT的方法,改善了評估方向圖的性能,節省了時間。圖4和圖5為局部優化最大適應度函數的收斂曲線,可以清楚地看到適應度函數的變化情況,當天線單元位置個體不斷地進化后,天線性能幾乎不再有所改善,副瓣電平降低為-21.71dB。進一步優化天線單元的激勵電流,可以看到峰值旁瓣比得到進一步改善,副瓣電平降低到-23.89dB,得到了比較好的結果,但是從仿真中可以看到在采用遺傳算法進行局部優化時很容易陷入局部收斂。圖6和圖7是采用了遺傳退火算法優化的結果,遺傳退火的初始溫度為T=50°。從仿真中可以看到副瓣電平降低到-26dB,比采用遺傳算法稀布改善了2.11 dB,具有更快的收斂速度。采用遺傳退火算法時能夠提高收斂速度,避免了局部收斂。
4 結束語
本文利用遺傳退火算法對32個數字陣列天線單元在64個位置進行了稀疏布陣,將天線單元位置,天線單元激勵電流作為優化變量,提供了更多的自由度,來改善數字陣列的副瓣電平,使副瓣電平達到期望的值,仿真中可以看到遺傳退火算法性能要優于遺傳算法,遺傳退火算法雖然加入了比較差的個體,但是它不但提高了優化的速度,節省了時間,而且避免了計算搜索過程陷入局部最優,甚至在所定義的適應度函數非連續、不規則和伴有噪聲的情況下也能以極大的概率找到最優解,非常適用于大規模陣列天線的處理。■
[1] Mailloux TJ.Phased ARRAY Antenna H andbook[M].Boston:A rtech H ouse,1994.
[2] Sam ii YR,M ichielssen E.Electromagnetic op tim ization by Genetic A lgorithm[M].New Yook:John W iley&Sone,1999.
[3] H olland JH.Genetic algorithms[J].Scientific American,1992(6):44-50.
[4] Johnson JM,Rahmat-Sam iiy Y.Genetic algorithms in engineering electomagnetics[J].IEEE Antennnas and propagation M agazine,1997,39(4):7-21.
[5] 王玲玲,方大綱.運用遺傳算法綜合稀疏陣列[J].電子學報,2003,31(12):2135-2138.
[6] 張子敬,趙永波,焦李成.陣列天線的遺傳優化[J].電子科學學刊,2000,22(1):174-176.
[7] 牛軼峰,伯曉晨,沈林成.基于可變模板的前視目標跟蹤算法[J].國防科技大學學報,2003,5(25):80-84.
[8] Wang LL,Fang DG,Sheng WX.Combination of genetic algorithm(GA)and fast Fourier transform(FFT)for synthesis o f arrays[J].M icrowave and Op tical Technology Letters,2003,37(1):56-59.

