基于遭遇點預測的比例導引與多平臺接力制導交接律設計

余名哲，張友安，錢 進

（1.海軍航空工程學院 控制工程系，山東 煙臺 264001；2.95737 部隊，重慶 402361）

為提高艦艇編隊的中遠程反導能力，實現區域防空的要求，需要艦空導彈具備超視距多平臺協同制導能力。

在有較大誤差的情況下，綜合各方面因素考慮，選取了對遭遇點的攻擊方式。這種攻擊方式目前文獻中并不多見，以往的遭遇點預測一般是根據導彈常用的視線法和比例導引法[1-2]解算導彈的運動學彈道來預測瞬時遭遇點的坐標。本文利用導彈、目標和遭遇點三方距離關系，按傳統比例導引解算的待飛時間[3-4]直接解算導彈對遭遇點的導引律。

為了實現不同平臺對超視距艦空導彈的協同制導，在導彈飛行過程中，相鄰平臺需要對導彈完成接力制導。在制導接力過程中，由于各平臺所提供的目標、導彈信息有所不同，因此各平臺的制導指令在交接點處發生突變。為實現彈道及制導指令的平滑過渡，需要設計交接律[5-6]。

1 基于遭遇點預測的比例導引律設計

根據導彈與目標的當前狀態，實時預測遭遇點。假設目標由當前時刻恒速運動到達遭遇點，導彈采用傳統比例導引[7]的方式到達遭遇點。當前時刻預測的相對運動關系如圖1所示。圖中，M表示導彈，T表示目標，T'表示預測遭遇點，R表示彈目距離，R '表示導彈到遭遇點的距離，L表示目標到遭遇點的距離，q表示目標視線角，q'表示遭遇點的視線角，設ox軸正向逆時針轉向為正。

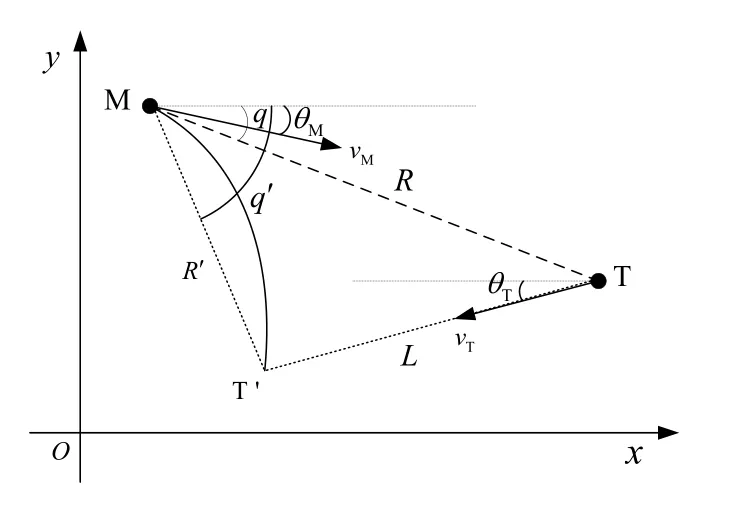
圖1 導彈、目標和預測遭遇點的相對運動關系

導彈對遭遇點進行比例導引，制導指令為

制導指令的解算，需要用到遭遇點的信息。下面根據遭遇點的預測方法，推導所需的遭遇點信息。

由導彈與遭遇點的相對運動關系，有

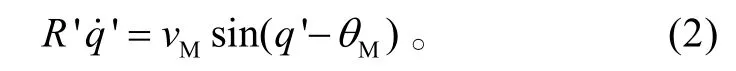
遭遇點 T'的坐標可以表示為

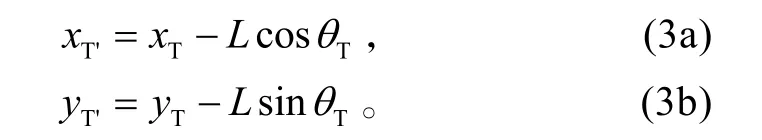
遭遇點的視線角 q' 具有關系

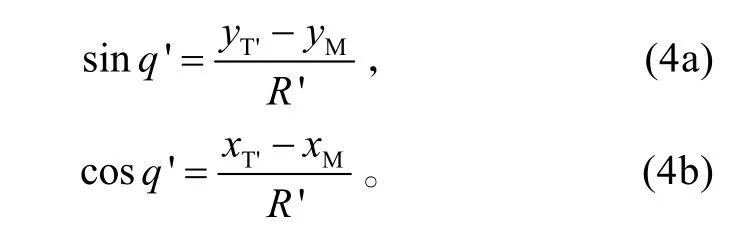
類似的目標視線角也有如下關系：

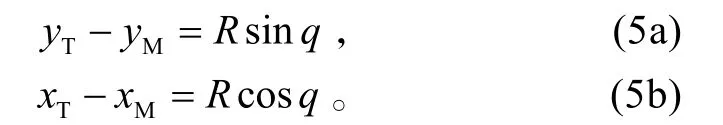
將式(3)代入到式(4)，可得

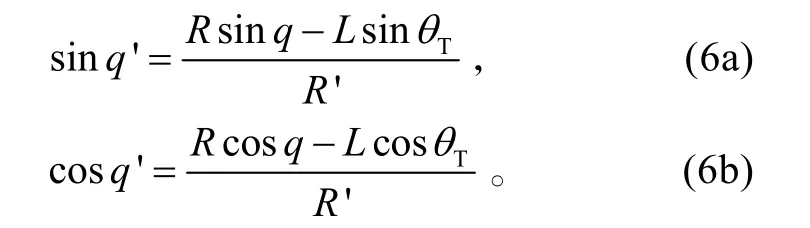
將式(6)代入到下式

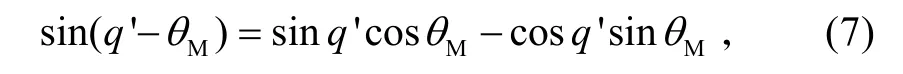
整理后可得

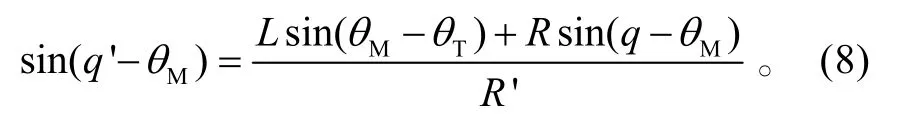
式中：

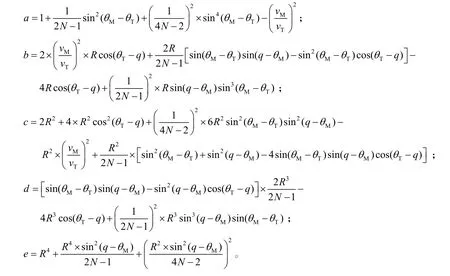
導彈到達遭遇點按照傳統比例導引解算的待飛時間為

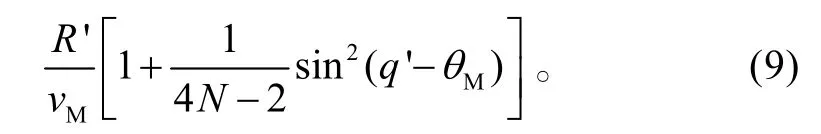
則導彈與目標同時到達遭遇點，須滿足

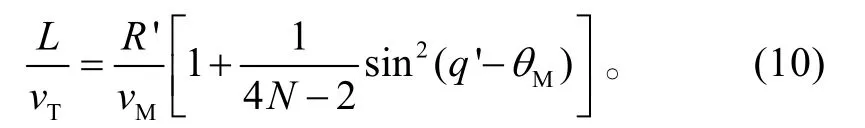
式(10)的左側表示目標到達遭遇點的時間，右側為導彈按照傳統比例導引到達遭遇點的時間，相當于導彈在當前時刻對固定點 T'的比例導引剩余時間估計。

對于導彈、目標與遭遇點所構成的三角形，由余弦定理有

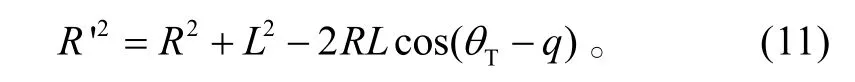
聯立式(8)、(10)、(11)可得

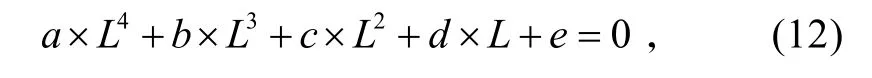
式(12)為僅含未知量L的一元四次方程，可實時求得數值解（摒棄不合理的解）。將所得的L代入式(10)可得 R'。這樣，將所得的R'代入式(8)，并將所得結果代入式(2)，最終可得制導所需的信息 q˙'。

一元四次方程的算法[7-8]可以利用待定系數法將一元四次方程化為兩個二次方程的乘積，通過解兩個二次方程達到四次方程的求解目標。

綜上，對遭遇點的制導指令所需信息為vM、Tv、Mθ、Tθ、R 與q。目標位于視距外，R 與q 不能直接獲得，但可由制導平臺所提供的目標與導彈坐標經式(13)計算得出，其余量均由制導平臺直接提供。

2 多平臺接力制導的交接律設計

導彈發射后，首先由發射平臺制導，導彈逐漸飛離發射平臺后，“制導權”交由距導彈較近的協同制導平臺實施，如需要，這種“制導權”的傳遞將繼續向下一協同制導平臺進行。網絡中的協同制導平臺可以是空中平臺也可以是水面平臺，如圖2所示。

設第i個協同制導平臺提供的導彈坐標為(xM,yM)，導彈速度為vM，彈道傾角為θM；目標坐標為(xT,yT)，目標速度為vT，目標彈道傾角為θT。

由于信息來源不同、數據傳輸過程中存在延遲及丟包等因素，各制導平臺對導彈制導過程中所提供的制導信息有所不同。

設第i+1個制導平臺所提供的信息相比第i個平臺有一增量，導彈坐標為(xM+?xM,yM+?yM)，導彈速度為vM+?vM，彈道傾角為θM+?θM，目標坐標為(xT+?xT,yT+?xT)，目標速度為vT+?vT，目標彈道傾角為θT+?θT。

根據第i個平臺與第i+1個平臺提供的目標與導彈的信息，在各突變信息[9]中引進平滑因子α。

在交接過程中，制導指令解算時所需要的導彈坐標取為(xM+ α? xM,yM+ α?yM)，導彈速度為vM+ α?vM，彈道傾角為θM+ α ?θM，目標坐標為(xT+ α? xT,yT+ α? yT)，目標速度為vT+ α? vT，彈道傾角為θT+ α ?θT。

當導彈由第i個平臺的制導區飛向第i+1個平臺的制導區時，導彈完成制導權的交接。交接條件：

式中：Pi1+表示導彈與第i+1個平臺的距離；ip表示表示導彈與第i個平臺的距離；0p為閾值。

平滑因子α可取為時間的函數，也可取為距離的函數，這里考慮是時間函數的情況。設交接起始時刻為t0，交接時間為T，則可設計平滑因子為：

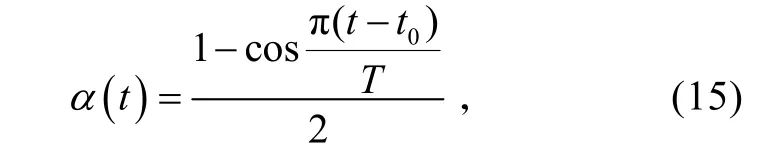
式中：t ∈ [t0,t0+ T]。

顯然，當t=t0時，制導指令的解算按照第i個平臺所提供的目標與導彈信息進行。

從t=t0開始，經時間T，在t=t0+T時實現制導指令的順利過渡，其解算最終按照第i+1個平臺所提供的信息進行。這種交接方式可以實現在規定的時間內完成彈道的平滑過渡，并在交接的初始時刻和結束時刻也能保證制導指令的平滑性。

3 仿真結果與分析

導彈初始位置 (xM,yM)為（1 000 m，20 000 m），初始彈道傾角 θM=30°，速度 VM為800 m/s；目標初始位置 (xT,yT)為（120 000 m，1 000 m），彈道傾角 θT=10°，以400 m/s的速度飛行。平臺交接時給定T=10s，p0=100，比例導引系數N=5。

仿真結果如圖3～6所示，圖6中不采用交接律的情況為測量的彈目軌跡。

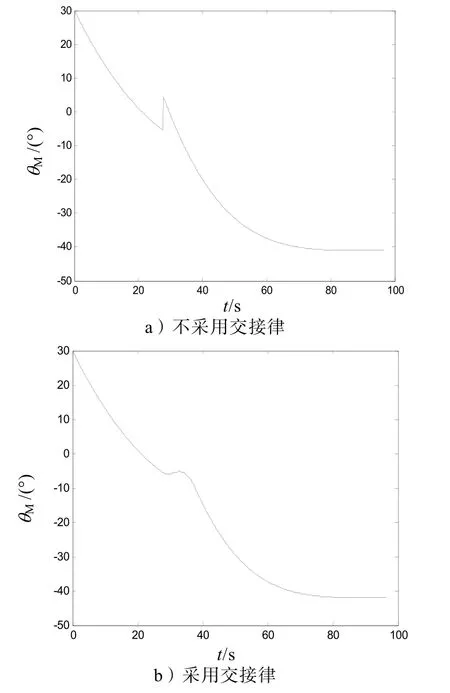
圖3 彈道傾角Mθ仿真曲線

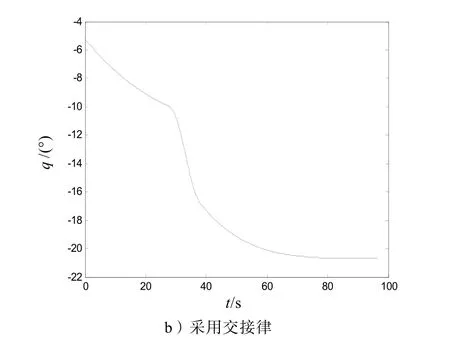
圖4 彈目視線角q仿真曲線

圖5 導引指令 aMn仿真曲線

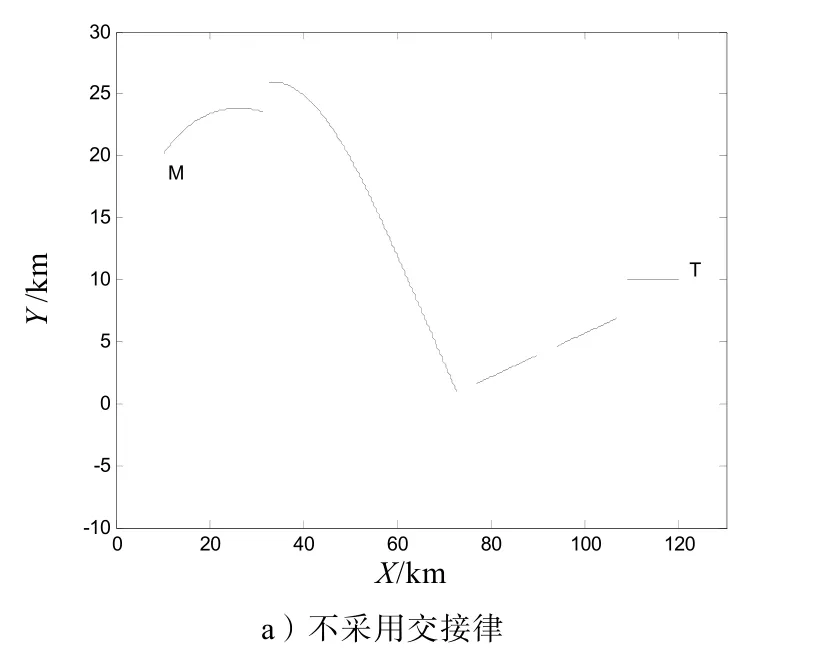
圖6 彈道軌跡仿真曲線

4 結束語

艦空導彈在空間中的制導過程在本文中把它分解到水平面內進行了分析。采用多平臺協同制導將擴大艦艇編隊防空區域，增加對空中來襲目標的攔截次數和攔截概率。本文設計的基于遭遇點攻擊的平臺交接率是有效的。今后對于平臺接力制導還有必要進行更深入的研究。

[1]王君,周林,雷虎民.地空導彈與空中目標遭遇點預測模型和算法[J].系統仿真學報,2009,21(1):80-83.

[2]一輝.當今俄羅斯主力艦艇防空導彈系統與集成方式解析[J].現代兵器,2008(1):6-11.

[3]馬國欣.多導彈時間協同制導方法研究[D].煙臺:海軍航空工程學院,2008.

[4]MIN-JEA TAHK,CHANG-KYUNG RYOO,HANG-JU CHO.Recursive time-to-go estimation for homing guidance missiles[J].IEEE Transaction on Aerospace and Electronic Systems,2002,38(1):13-24.

[5]張友根,張友安,施建洪,等.基于雙圓弧原理的協同制導律研究[J].海軍航空工程學院學報,2009,24(5):537-542.

[6]劉興堂.導彈制導控制系統分析、設計與仿真[M].西安:西北工業大學出版社,2005.

[7]樊正恩.一元四次方程的一種新解法[J].數學學習與研究:教研版,2009(4):93-96

[8]智海章.一元四次方程的一種解法探討[J].數學教學,1988(5):2-3.

[9]張建偉,黃樹彩,韓朝超.基于Matlab的比例導引彈道仿真分析[J].戰術導彈技術,2009,21(3):60-64.