港口集裝箱空箱調度的遺傳算法優化

楊 揚，王 迪

（1.廈門海洋職業技術學院，福建 廈門 361012；2.大連海事大學 交通運輸管理學院，遼寧 大連 116026）

隨著經濟全球化、貿易國際化的深入發展，國際海運業得到迅猛發展，集裝箱運輸具有運量大、裝卸及疏運快、節約包裝材料、安全便捷等優點，越來越多的散雜貨選擇集裝箱運輸，所以，集裝箱運輸已成為全球國際貿易中最重要的運輸方式之一。然而集裝箱海運業的繁榮對其自身的經營管理模式及網絡結構提出了更高要求，高效、有序的港口集裝箱運輸網絡有待完善與優化。由于地區間經濟貿易的不平衡性以及船運公司集裝箱管理水平存在差異，空箱調運在整個集裝箱運輸系統中占據了大量比重。研究如何減少集裝箱空箱調運，對于促進集裝箱運輸快速發展、協調多式聯運、提高企業經濟效益具有重要意義。

由于空箱調運產生的成本對船公司的運營收益產生了很大影響，船公司對該問題非常重視，并引發了學術界的研究興趣。集裝箱調運問題主要研究的是何時從何地將多少數量的空箱通過何種運輸方式調運到有需求的指定地點。空箱調運問題具有隨時間推移供需地發生變化的動態性，箱種、節點、運輸工具眾多的復雜性，以及空箱需求與供給的隨機性和運輸能力及供應時間的限制性等多方面特性。由于空箱調運問題中過程參數、不確定因素眾多使問題相當復雜。當前國內相關專家、學者對此問題進行了較多的研究，取得了相當的成果，并對實際運營過程做出有益的參考。其中，施欣對海上空箱調運的過程進行分析，并建立了系統優化模型[1]；劉恒江等以航線經營人為主體，建立了空箱調運的Petri網模型[2]；周紅梅等借鑒了鐵路空車調度優化模型，建立了海運空箱調運優化模型[3]；Florez等建立利潤優化模型來研究遠洋航運企業空箱租賃和重新配置問題[4]；Shen等構建了海運空箱調運決策支持系統[5]。

然而這些研究在建立模型時都進行了大量假設，考慮因素較少，與實際系統相差較遠，大大降低了模型的實用性。本文擬在考慮多箱種的情況下，建立合理的空箱調運動態優化模型，并運用遺傳算法進行優化求解，并用某港口實例數據對模型進行了驗證，證明了模型的正確性和遺傳算法的有效性。

1 空箱調運模型

本文將建立多箱種情況下的空箱調運模型，目標函數為在滿足重箱運輸的前提下，使空箱調運的總費用最少。總費用由以下幾種費用組成：空箱的運輸費用、在各節點的儲存費用以及租箱費用。

1.1 模型假設

（1）每一期每個節點的空箱數量已知、每個節點的空箱需求量已知；（2）不考慮集裝箱的維修、報廢情況，即所有集裝箱均是可用的；（3）不存在轉運現象，空箱是直接由供應地向需求地的直達運輸；（4）各航線的集裝箱運輸不允許不同箱型相互替換；（5）考慮兩種箱型：20英尺和40英尺；（6）空箱調運決策期為1周（5天計算），決策間隔以天計算；（7）需求客戶的需求必須得到滿足，不存在棄貨問題；（8）只有到時段末還未運送的集裝箱發生堆存費用。

1.2 模型建立

根據以上假設及其空箱調運實際情況，可以建立如下空箱調運模型，相關參數和變量規定如下：

1.2.1 參數

T：為計劃周期；Dt：t時段時所有需求點的集合；St：t時段是所有供給點的集合；：t時段節點i缺k種箱型的數量；：t時段節點j能供應k種箱型的數量；M：所有供給點和需求點的集合；K：各種箱型的集合，包括20英尺和40英尺兩種；：在時段t從i到j運輸第k種箱型的單位運輸費用；：在時段t從i到j運輸第k種箱型的箱量；：在時段t節點i的第k種箱型的存儲量；：節點i的存儲能力限制；：在時段t節點i的k種箱的單位存儲費用；：在時段t節點i和j之間由k種箱運輸的調運量；τij：從節點i到j得運輸時間；：運輸能力限制；：系統外調箱的單位費用；：系統外調箱量；：t時段m點本地產生的空箱。

1.2.2 目標函數

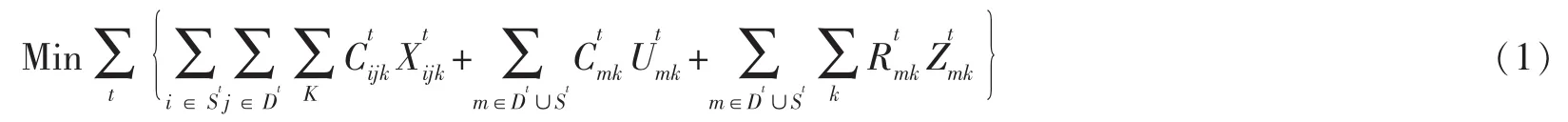
目標函數考慮各期在需求客戶和供給客戶之間的空箱調運費用最少。

1.2.3 約束條件

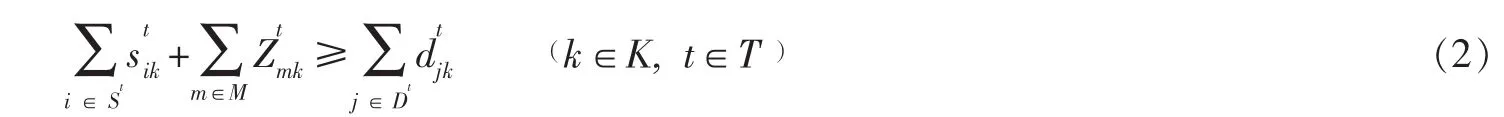
約束條件（2）表示客戶的集裝箱需求量必須滿足。

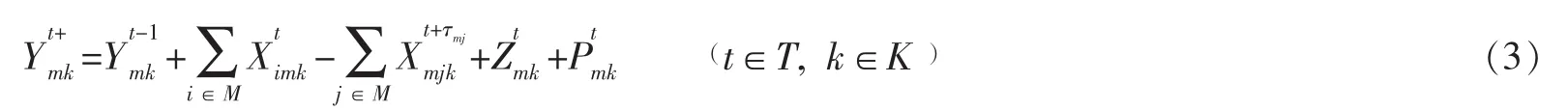
約束條件（3）表示各時段末各節點處的空箱庫存。

約束條件（4）表示各時段供應節點的供應量。

約束條件（5）表示在各個時段，節點之間的運輸量不能超過該種運輸方式的運輸能力。

約束條件（6）表示各節點的存箱量不能超過該點的容量。

2 遺傳算法原理

遺傳算法（Genetic Algorithms，GA）是由美國Michigan大學的John H.Holland教授創建的，它模擬了自然選擇和進化過程中的繁殖、雜交和突變現象。其基本思想為：按照“適者生存”和“優勝劣汰”的原理，從優化問題一個種群（即一組可行解）開始，逐代進化產生出越來越好的一個新的種群（一組的可行解）。在每一代，根據個體（可行解）適應度（目標函數值）的優劣挑選一分優良個體復制（繁殖）到下一代，被選擇的個體經過交叉和變異算子的作用生成新的一代，新的個體由于繼承了上一代的一些優良性狀，因而在性能上優于上一代，這個過程將導致種群類似自然進化一樣，子代種群比父代種群更加適于環境，也就是生成新的可行解優于舊的可行解，最后，將整個進化過程中最優個體作為問題的最終解。

由于遺傳算法對適應度函數沒有連續可微的要求，具有高效的全局優化能力，并且其操作對象是編碼個體，可以處理諸如矩陣、樹和圖等結構形式的對象，因此在解決高維復雜優化問題上顯示出很強的生命力，在實際中得到了廣泛的應用。基于遺傳算法的特點和空箱調運問題的特征，本文采用了遺傳算法對該問題進行優化。

3 算法描述及其實例

3.1 算法設計

（1）編碼方案：根據本文模型決策變量的特征，本文采用多維的實數編碼形式。例如，用實數集合M=｛1, 2 ,…,n｝表示港口集合，K=｛1,2｝表示箱型（20英尺和40英尺），則t時段的一個可行解表示為：

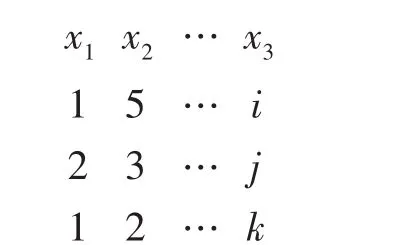
這個解直觀的表達就是：港口1向港口2調運x1個集裝箱（箱型是20英尺），港口5向港口3調運x2個集裝箱（箱型是40英尺），……。

（2）選擇：采用輪盤賭選擇算子，這雖然增大了遺傳算法的隨機性，但保證群體的多樣性，使算法不至于過早收斂。

（3）交叉：交叉運算是遺傳算法區別于其他進化算法的重要特征，它在遺傳算法中起關鍵作用。由于基本交叉算子單點交叉、多點交叉不能滿足本文空箱調運問題的特殊性要求（它們都會產生大量不可行解），所以本文采用的交叉算子為循環交叉算子，該算子能修正交叉過程中生成的不可行解。

（4）變異：變異是指將個體編碼串中的某些基因值用其它基因值來替換，從而形成一個新的個體。遺傳算法中的變異運算是產生新個體的輔助方法，它是必不可少的一個運算步驟。變異本身是一種全局隨機搜索，與選擇算子結合在一起，保證了遺傳算法的有效性，使遺傳算法具有全局的隨機搜索能力，同時使得遺傳算法保持種群的多樣性，以防止出現非成熟收斂。本文在考慮編碼設計及問題實際的情況下采用均勻變異算子對種群進行變異操作。

算法流程圖如圖1所示。

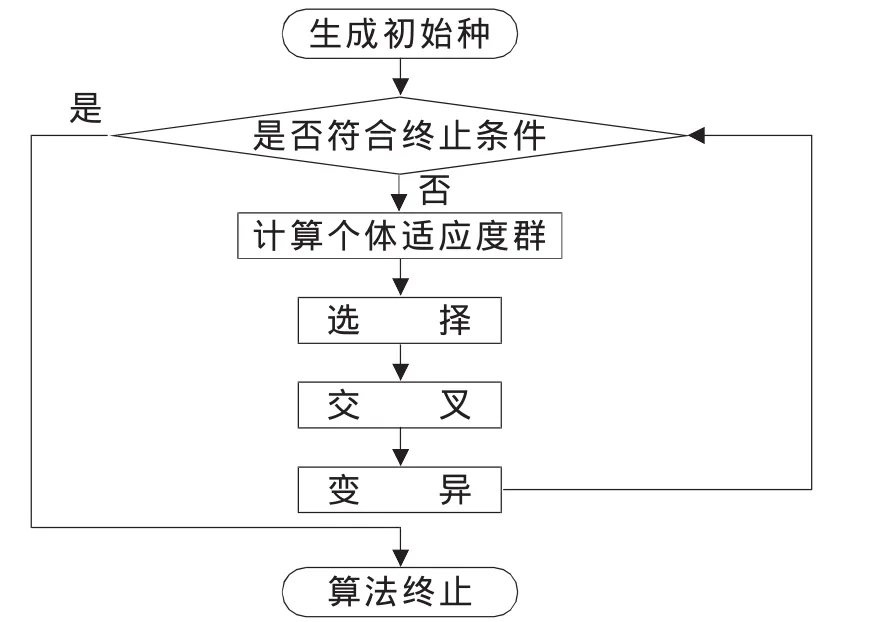
圖1 算法流程圖

3.2 實例

本文考慮六個港口的空箱調運問題，算例中假設運輸能力和堆存能力無限制，只考慮一種箱型（40英尺），在一個計劃期內，航線掛靠順序不變。這六個港口的運輸網絡模型如圖2所示。港口運輸時間、費用如表1所示。港口初始庫存和各時段需求狀況分別如表2、表3所示。

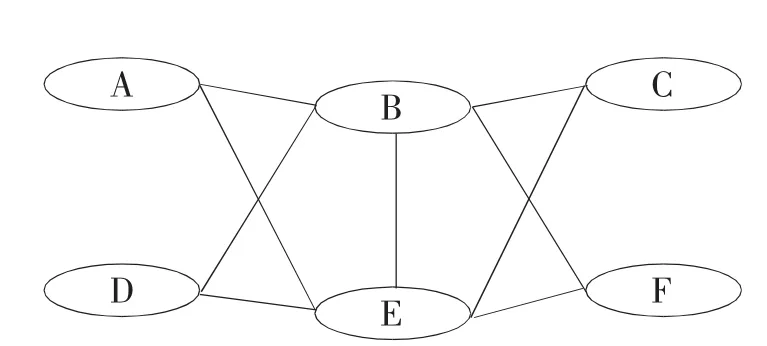
圖2 運輸網絡圖

表1 港口間的運輸時間、費用表 單位：天、$/TEU

表2 港口空箱基本數據

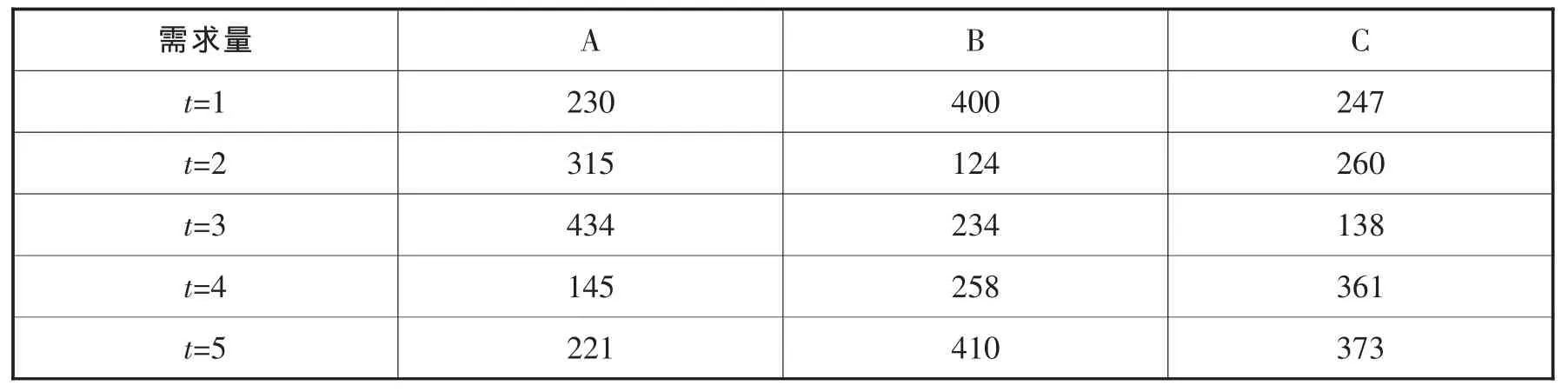
表3 港口需求表 單位：TEU

該算法利用matlabR2009程序實現，取最大迭代數G=500，本文針對不同種群規模進行了大量測試，結果表明當種群規模N=100左右時效率最高；對交叉概pc為0.7、0.8、0.9分別進行了10次試驗發現交叉概率的變化對算法的效率影響并不是很大，所以取交叉概率pc=0.8。最后，我們進行了三組實驗，分別取變異概率pm為0.001、0.01、0.1，由實驗結果分析得出當變異概率時pm=0.01，效果最好。最終得出最優解，第一期調運結果：由港口B至A調運空箱80個，由E至C調運空箱163個，由F至E調運空箱10個，總費用為6 119美元，其中庫存費用為2 158美元；第二期調運結果：由B至A調運空箱75個，由E至A調運空箱9個，由C至E調運空箱13個，總費用為5 051美元，其中庫存費用為3 014美元；第三期調運結果：由B至A調運空箱119個，由E至C調運空箱110個，總費用為6 734美元，其中庫存費用為3 065美元；第四期調運結果：由B至C調運空箱24個，由A至E調運空箱23個，由D至E調運空箱200個，總費用為8 738美元，其中庫存費用為2 065美元；第五期調運結果：由B至A調運空箱76個，由E至C調運空箱125個，由D至E調運空箱46個，總費用為6 938美元，其中庫存費用為3 075美元，租箱費用為315美元。這一周期的總費用為33 580美元。

4 結 論

本文力求與實際情況接近，充分考慮了空箱調運問題中多箱型的現實情況，應用動態規劃的思想，建立了多箱型的集裝箱空箱調運優化模型。最后，本文運用遺傳算法對所建立的模型在matlab平臺下進行了編程仿真，為港口間空箱調運提供了具體的方案。本文模型的目的在于提高航運企業的空箱調運管理水平和調運效率，節省不必要的運輸費用。

[1]施欣.集裝箱海運空箱調運優化分析[J].系統工程理論與實踐，2003(23):70-75.

[2]劉恒江，施欣.基于Petri網的集裝箱空箱調運方針分析[J].交通運輸工程報，2002,2(3):97-102.

[3]周紅梅，方芳.航運集裝箱空箱調運優化模型的研究[J].武漢理工大學學報，2003,2(7):384-387.

[4]Florez.H.Empty container Repositioning and Leas2ing:An Optimization Model[R].Ph.D Dissertation,Polytechnic Institute of New York,New York,1986.

[5]W.S.Shen,C.M.Khoong.A DSS for empty container distribution planning[J].Decision Support Systems,1995(15):75-82.

[6]王斌.海運空箱調運模糊優化研究[J].港工技術，2007,8(4):11-13.

[7]王小平，曹立明.遺傳算法—理論、應用與軟件實現[M].西安：西安交通大學出版社，2002.

[8]趙道致，黃健.基于海陸運整體成本的集裝箱空箱調運優化研究[J].北京交通大學學報，2008,7(4):48-52.