網絡搜索鏈接技術的研究*

官 斌

(武漢市74223信箱 武漢 430074)

1 引言

隨著互聯網絡的日益迅猛增長,互聯網絡已成為世界上規模最大的信息源之一。在如此巨大的數據海洋中尋找用戶所需要的信息已不是人力所能勝任的工作了,因而搜索引擎已經作為互聯網上最有效的信息獲取工具而為人們廣泛接受。

不同于傳統的信息檢索(圖書館資源檢索),互聯網不僅包含了大量的內容信息(包括文字、圖像、聲音、視頻),而且還包含了復雜的結構信息(如超鏈接關系,網站的組織結構等等)。對互聯網結構信息的利用能夠很大程度上決定一個搜索引擎性能的好壞。因此,鏈接分析(link analysis)已成為互聯網檢索領域一個很熱的話題,吸引了眾多研究者的關注。本文介紹了從1998年以來鏈接分析技術的進展,并在此基礎上指出了進一步的研究方向。

2 鏈接分析的興起:兩大經典算法的提出

1998年是互聯網搜索歷史上最有紀念意義的一年。鏈接分析的兩大經典算法都于該年提出:HITS和PageRank。正是由于鏈接分析的運用,是互聯網搜索的準確程度有了一個質的飛躍。下面我們簡單介紹一下這兩個算法。

2.1 PageRank算法

PageRank[2]是由斯坦福大學的兩個博士研究生Sergey Brin和Lawrence Page于1998年提出,Google即為該論文的原型系統,如今已發展成為世界上最好的搜索引擎。

PageRank算法的基本思想相當簡單。PageR-ank認為,每個網頁的重要程度是不一樣的。如果一個網頁被很多網頁指向,那么該網頁很可能非常重要;另外,一個重要的網頁所指向的網頁也很可能非常重要。PageRank的基本原理可以用馬爾可夫隨機游走模型來解釋。PageRank模仿一個用戶在互聯網上瀏覽行為,在當前時刻,該用戶以一定的概率q跳轉到任意一個網頁,或者以概率1-q跳轉到當前網頁所指向的某一網頁。該過程可以用一個馬爾可夫鏈來建模,互聯網中的每一個網頁就是馬爾可夫鏈中的一個狀態。該馬爾可夫鏈平穩時每個狀態停留的概率即反映了相應網頁的重要程度。

下面我們介紹一下PageRank算法的具體實現。如果整個網絡有n個網頁,將這個網絡看成有n個節點的有向圖,圖上的每條有向邊代表了互聯網上一個超鏈接。該圖的鄰接矩陣A記為:將鄰接矩陣的每一行行和歸一化,我們可以得到該隨機跳轉(馬爾可夫鏈)的概率轉移矩陣 ˉA。為了保證該馬爾可夫鏈能夠收斂到一個平穩狀態,該馬氏鏈必須滿足非周期不可約兩條性質。然而對于一個實際的網絡,并不一定能夠滿足這兩個條件。這里PageRank算法對概率轉移矩陣ˉA進行了平滑處理其中U是一個n*n的矩陣,并且每一個元素都為1/n。其中α是一個經驗常數[2],建議使用0.85。進行了平滑之后,就能夠確保隨機跳轉的平穩狀態存在且唯一。將該馬氏鏈平穩狀態每個節點停留概率記為πi,那么πi就體現了網頁的重要程度。πi越大,該網頁越重要。πi可以由如下公式計算得到

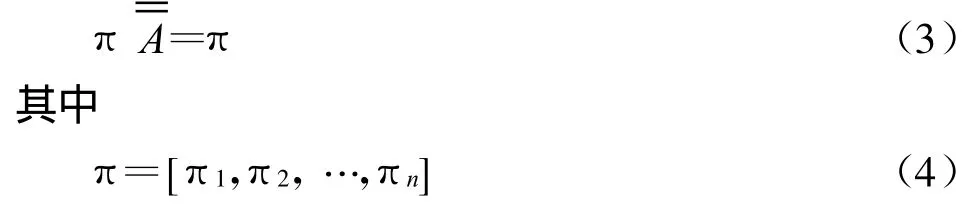
也就是說,整個網絡的PageRank向量就是平滑后的概率轉移矩陣最大的左特征向量。由于鄰接矩陣的規模相當龐大(對于現在的互聯網,網頁的數量都在十億的規模),因此人們一般不是直接求的特征向量,而是采用如下的冪法迭代

直到收斂為止。

2.2 HITS算法

不同于PageRank算法用一個量來衡量一個網頁的重要性,HITS用兩個量來衡量一個網頁的好壞:Hub值和 Authority值。直觀的理解,Authority值反映了網頁本身質量的好壞,如果該網頁自己的內容很好,則她的Authority值就可能很高;Hub放映了網頁本身作為路由的好壞,如果該網頁所指向的很多網頁的質量都很高,那么該網頁本身的Hub值就可能很高。如果我們記網絡的Hub向量為h,Authority向量為a(和 PageRank向量類似,hi和ai分別表示了網頁i的Hub值和Authority值),那么這兩者之間的關系可以表示為

通過以上兩式迭代達到最終收斂時,就可以得到整個網絡的Hub向量h和Authority向量a。

3 鏈接分析的高潮:兩大算法的各種變種

隨著兩大算法的提出,人們發現他們的確對搜索性能有很大的提高,因而大大激發了人們對鏈接分析研究的熱情,對PageRank和HITS進行了廣泛的研究,提出了各種各樣的推廣和變種。由于該方面的文獻很多,這里只是選取其中幾個最有代表性的工作進行介紹。

3.1 主題敏感的PageRank

在前面我們提到PageRank算法不依賴于查詢詞,對每一個網頁只計算一個PageRank值來表示它的重要性,這樣整個網絡只有一個PageRank向量[5]。提出了主題敏感的PageRank算法。該算法的基本思想是選定一定數量的主題,(對每一個主題計算一個PageRank向量,這樣每一個網頁相應于每一個主題都有一個 PageRank值。當來了一個查詢詞后,根據該查詢詞和每個主題的相關程度將任意一個網頁對應于不同主題的PageRank值組合起來,就得到該網頁相應于這個特定詞的PageRank值。需要指出的是,不同查詢詞的組合方式不同,需要在搜索時實時計算。

可以看到,主題敏感的PageRank對不同的查詢詞區別對待,因此計算出來的PageRank值會比標準的PageRank值更加準確。

3.2 塊級別的鏈接分析

鏈接分析的大部分工作都是網頁級別的,也就是把每一個網頁當作圖中的一個節點,然后考察每個節點的屬性。實際互聯網中的網頁往往含有多種意義,網頁的不同部分所反映的內容不同。例如每個網頁的中間部分的內容往往是該網頁所想表達的真正意思,網頁的最下面往往都是一些網站的版權信息,網頁的左右的側邊欄則往往是一些導航鏈接或者廣告。因此文獻[3]認為網頁的每一部分的重要性程度不同,他們提出了塊級別的鏈接分析算法。塊級別的鏈接分析算法的基本思想實現對每個網頁分塊,然后網頁中的每一個塊作為一個節點構造塊級別的圖,然后在該圖上應用PageRank或HITS算法。

塊級別的鏈接分析算法由于對網頁的每一部分區分對待,因此能夠很大程度上抑制噪聲的影響。特別是一些網頁經常在邊沿部分添加大量的惡意鏈接,而塊級別的鏈接分析算法恰好能夠把網頁的這些部分和重要內容部分區別對待。

3.3 考慮網絡層次結構的鏈接分析

無論是網頁級別的鏈接分析還是塊級別的鏈接分析,他們都把網絡看成一個平片結構,網絡中的節點本身是無法區分的,除了他們連接的邊不同之外。然而實際的互聯網是層次化結構的,近年來有很多文獻[4,11～12]利用該特點來更好地進行鏈接分析。

將萬維網看成平面化的網絡進行連接分析有兩個問題:第一是每個節點(網頁)的連接很稀疏;第二是無法很好的處理新出現的網頁,因為很少會有鏈接指向一個剛剛出現的網頁,盡管這個網頁的內容可能會很好。因此文獻[11]提出了一種鏈接分析的算法,綜合利用了萬維網的層次化結構和超鏈接結構。他們構建出的萬維網拓撲結構如圖1所示。該網絡拓撲結構主要有兩層,上層反映的是站點之間的鏈接關系,下層反映的是每個站點內部的層次結構關系。根據該拓撲結構,他們定義了一個新的隨機游走模型。

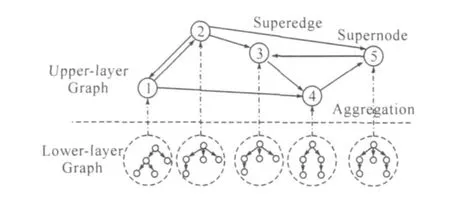
圖1 層狀互聯網拓撲結構

4 鏈接分析的深入:計算與理論

隨著鏈接分析算法的日益增多,人們不再局限于僅僅是對PageRank算法和HITS算法進行簡單的推廣或改動,進而開始研究算法本身的一些性質,主要是兩方面的內容:計算和理論。在第一節中我們已經指出,相對而言PageRank算法更具理論基礎,因此鏈接分析的深入研究主要是針對PageRank算法。

4.1 PageRank的快速計算

PageRank算法由于是在整個萬維網上進行迭代計算,因此計算的規模相當龐大,如何進行快速的計算是一個非常重要的問題。

文獻[6]中提出了一種二次外推法來加速PageRank的計算。正如在第一節中所述,原始的PageRank的計算采取的是乘冪迭代法,最后迭代收斂到概率轉移矩陣的最大特征值所對應的特征向量。文獻[6]中的二次外推法從迭代向量中周期性減去非最大特征向量的成分,因而能夠大大加快PageRank的收斂速度。Sepandar D.Kamvar等人在文獻[6]中巧妙的利用概率轉移矩陣的最大特征值為1這一特點來計算其他的非最大特征向量。他們的實驗表明,在一個8千萬網頁的互聯網上,該算法對 PageRank的計算可以加速到 25%～300%。

文獻[9]中提出了另外一種方法來加速PageRank的計算。他們的核心思想是在PageRank的每一次迭代中相鄰節點間傳遞的不再是各個節點的概率值,而是節點概率的改變值。這樣一種方法使得節點在更新它們的概率值是有很大的自由度,并將該問題轉化為矩陣優化問題,這樣就帶來了一系列的好處,如快速收斂性,高效的增量式更新,以及穩定的分布式實現。ˉA中實驗表明,在一個3千4百萬網頁的互聯網上,該算法能夠有效提升PageRank計算的性能。

4.2 PageRank的理論分析

由于PageRank算法的計算是要通過不停的迭代直到收斂為止,這樣就產生了很多數學分析上的理論問題:該迭代的收斂性能如何?收斂速度如何?對擾動的敏感程度如何?目前已經開始有研究人員注意到這些問題,并做出了一些很好的工作。

從式(2)可以看出,PageRank中的馬氏鏈的概率轉移陣是由兩部分共同決定的,一部分是網絡本身的結構即ˉA,另一部分則是均勻矩陣U,而經驗常數α則決定了這兩部分之間的比重。文獻[2]中雖然建議α取0.85,但是并沒有解釋為什么要選擇這樣一個值,并且人們也發現,不同的α不僅對最終每個網頁的PageRank值會帶來很大的影響,甚至會扭轉網頁之間相對重要的順序文獻[8,10]。那么α究竟該如何選擇?有沒有什么理論依據?文獻[1]中將最終的PageRank向量作為α的一個函數,首次對PageRank向量隨著α的改變進行了嚴密的數學分析。

注意α的取值為半開區間[0,1)。給定一個α值,我們就可以得到一個 PageRank向量r(α)。文獻[1]中首先證明了如下極限的存在

進而文獻[1]文發現雖然當α趨近1時,該馬氏鏈越來越接近準確的網絡連接圖,但是得到PageRank向量卻并不能帶來很好的網頁排序。另外,文獻[1]文還給出了PageRank向量r(α)對 α的任意階倒數的解析形式,為PageRank算法的理論分析提供了堅實的基礎。

5 鏈接分析的展望:搜索引擎的優化與作弊

由于鏈接分析算法在搜索引擎中占到了很重要的作用,導致了很多人專門針對網站的超鏈接進行優化或者作弊,并給搜索引擎的性能帶來惡劣的效果。Google作為全球最大最成功的搜索引擎,已經把如何應對搜索引擎作弊列為當前最重要的挑戰。

我們可以看出,鏈接分析這幾年來取得了很大的進展,但是也遇到了一些問題。例如很多搜索引擎優化或作弊專門針對不同的鏈接分析出發:為了提高一個網頁的PageRank值在很多網頁上發布自己的網址,這樣就可以增加指向自己的鏈接;同樣為了提高網頁的Hub值而在網頁上增加很多和內容完全不相關的超鏈接,這樣來增加網頁指出去的鏈接。

因此我們預言,鏈接分析算法下面一個很重要的研究問題就是如何有效地抵制搜索引擎優化或作弊。具體說來,我們認為可以從以下兩個角度來進行研究:

1)改進現有鏈接分析算法,使之能夠發現作弊的網頁;

2)提出新的鏈接分析算法,而這些因為考慮到了搜索引擎作弊的可能而很難被一般的作弊方法干擾。

[1]P.Boldi,M.Santini,S.Vigna.PageRank as a function of the damping factor[C].WWW2005

[2]S.Brin,L.Page.The anatomy of a large-scale hypertextual Web search engine[C].WWW1998

[3]D.Cai,X.F.He,JR Wen,et al.block level link analysis.SIGIR2004

[4]G.Feng,T.Liu,X.Zhang,et al.Level-Based Link Analysis[C].APWeb2005

[5]T.H.Haveliwala.Topic-Sensitive PageRank[C].WWW2002

[6]S.D.Kamvar,T.H.Haveliwala,C.D.Manning,et al.Extrapolation Methods for Accelerating PageRank Computations[C].WWW2003

[7]Kleinberg,J.Authoritative Sources in a Hyperlinked Environment[J].Journal of the ACM,1999,46(5)

[8]A.N.Langville,C.D.Meyer.Deeper inside PageRank[J].Internet Mathematics,2004,1(3)

[9]Frank McSherry.A uniform approach to accelerated PageRank computation[C].WWW2005

[10]L.Pretto.A theoretical approach to link analysis algorithms[D].2002

[11]G.Xue,Q.Yang,H.Zeng,et al.Exploiting the Hierarchical Structure for Link Analysis.SIGIR2005

[12]H.Yan,T.Qin,T.Liu,et al.Calculating Webpage Importancewith SiteStructureConstraints[C].AIRS2005