磁懸浮系統的變速趨近律滑模控制

陳衛兵，茅靖峰

（1. 南通職業大學，南通 226007 ；2. 南通大學，南通 226019）

磁懸浮系統的變速趨近律滑模控制

陳衛兵1，茅靖峰2

（1. 南通職業大學，南通 226007 ；2. 南通大學，南通 226019）

0 引言

磁懸浮系統是一個高度非線性，參數時變及開環不穩定的系統，傳統的磁懸浮控制器設計方法是在系統平衡點附近局部線性化的基礎之上，應用線性系統的方法來設計控制器[1,2]。但當磁懸浮系統在大范圍承載力及工作氣隙變動條件下工作時，傳統的基于平衡點參數優化的PID控制器不易得到理想的控制效果。多種非線性控制方法如模糊PID控制[3]、反饋線性化技術[4]、魯棒控制[5]、滑模控制[6]、神經網絡方法[7]、后推控制[8]等被用來克服上述問題。

滑模控制（SMC）無需精確的對象模型，可根據系統當前的狀態，以躍變的控制方式迫使系統沿設定的“滑動模態”運動。具有響應速度快、對參數及外加干擾不靈敏、控制器實現簡單等優點[9,10]。但常規滑模控制信號的抖振特性，會導致懸浮體穩態懸浮時的位置振顫現象。本文應用指數趨近律結合一種與狀態范數成比例的變速趨近律方法設計磁懸浮系統滑模控制器，目的是消弱控制輸出信號的抖振，增強系統的動、靜態性能。

1 數學建模

本文研究的單自由度磁懸浮系統的結構原理如圖1所示。

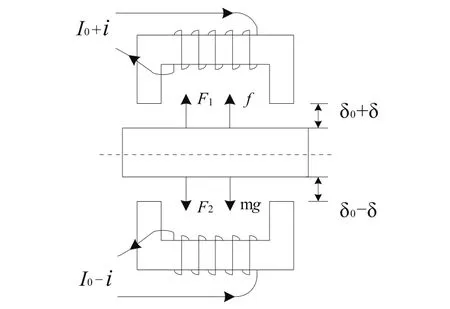
圖1 單自由度磁懸浮系統結構原理圖

圖1中，懸浮體是質量為m(kg)的整體鋼盤，置于兩個電磁鐵之間，當懸浮體處于平衡位置時，與上下電磁鐵之間的氣隙相等，均等于δ0(m)。設上下電磁鐵的結構和參數完全一致，線圈匝數均為N，單磁極面積為A0(m2)，采用電流疊加型差動驅動方式，初始偏置電流為I0(A)。則在只考慮氣隙磁通均勻，忽略鐵心磁阻、漏磁及渦流損耗等情況下，懸浮體受到的電磁合力可表述為

式中，F1、F2分別為上下電磁鐵的電磁吸力；μ0=4π×10-7為真空中的磁導率；δ為懸浮體偏離平衡位置的位移量；i為電磁鐵控制電流，i=Im+ic，Im為為克服懸浮體自重而加的初始平衡控制電流分量，ic為由δ引起的控制電流分量。

由圖1可得懸浮體的運動力學方程為

式中，g=9.8m/s2；f為擾動力。

將式(1)在平衡位置δ=0和ic=0附近作泰勒展開，略去高階無窮小量后，帶入式(2)式可得懸浮體的近平衡點運動方程為

2 滑模控制器設計

滑模變結構控制器設計包括兩個相對獨立的步驟：設計切換函數s(x)，使它所確定的滑動模態漸進穩定且具有良好的動態品質；設計控制律u±(x)，使到達條件得到滿足，從而在滑模面s(x)=0上形成滑動模態。

對于線性系統(4)，選取線性切換函數

式中，c1＞0為滑模面系數，決定最終滑模狀態的品質。選取指數趨近律

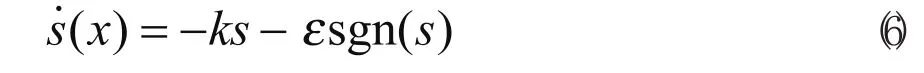
式中，ε，k＞0，k的作用是改善系統的動態品質，適當調節該參數能夠改變系統向滑模面的趨近速度；符號函數的增益參數是系統克服攝動及外干擾的主要參數。

由式(5)和式(6)可解出變結構控制律

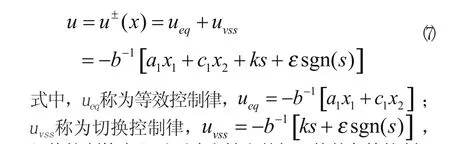
切換控制律實現對不確定性和外加干擾的魯棒控制。選取Lyapunov函數

因此，對(5)式求導，并由(4)式和(7)式得

故，當取ε＞max|df|時，變結構控制律(7)滿足滑動模態的到達條件，能夠驅使系統沿著滑模線s趨近于平衡原點。考慮到廣義對象模型參數a、b和f隨時間t的攝動，實際控制律ε參數應取足夠大，以實現對外干擾和參數攝動的不變性。

顯然，符號函數增益ε是系統克服攝動及外干擾的主要參數，ε越大，系統克服攝動和外干擾的能力就越強。但在增大ε的同時也導致了系統抖振幅度的加大。

為了消弱抖振，考慮變速趨近律[10,11]

變速趨近律(11)能夠將系統引導到滑動模態上，并在系統狀態軌跡向滑模面趨近過程中，||x||1的幅值逐漸衰減并很快趨向于零，最后使穩定于平衡原點。

為了避免滑動模態初期，過大的||x||1產生大幅度的控制量抖振，變結構切換控制律uvss可選用指數形式趨近律和變速趨近律的組合形式[11]。即在滑模運動前期采用指數趨近律，在滑模運動后期和穩定階段，采用變速趨近律，兩種趨近律通過判別相跡點與滑模面的距離|s|進行切換。最終得出系統切換控制uvss的形式為

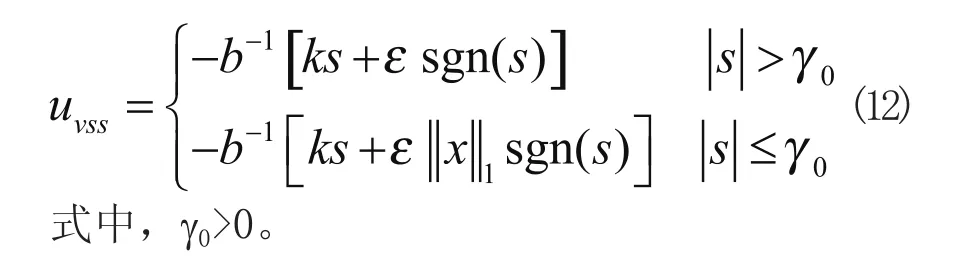
3 仿真實驗

實驗用磁懸浮系統的機械及電氣參數如表1所示。

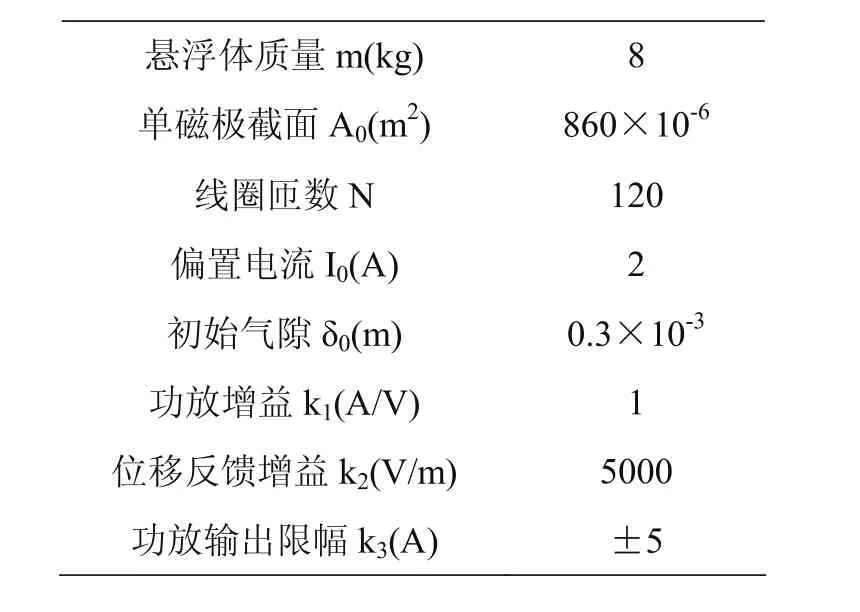
表1 磁懸浮系統參數

滑模控制器參數設計為：c1=400，k=800，ε=Fmax/m=86.4566，γ0=0.01。為了進行對比，設計了磁懸浮系統PID控制器，PID參數按照文獻[2]給出的方法進行整定，其中選取閉環等效位移剛度kx=4kδ，阻尼比ζ=0.8，可計算得到Kp=6.6667，Td=0.0012s，Ti=0.016s。

圖2、圖3和圖4分別為磁懸浮系統在PID、常規滑模和變速趨近律滑模控制下，磁懸浮系統空載起浮過程的位移響應曲線、控制量輸出曲線和相軌跡曲線。

由圖2可以看出，變速趨近律滑模控制和常規滑模控制均能使系統快速無超調起浮，動態性能優于PID控制。但在穩態區間，常規滑模控制較大的符號增益使系統控制量高頻率大幅值抖動（見圖3(b)），導致懸浮體在平衡位置上形成了幅值±1.3μm的位移振顫（見圖2(b)）。由圖4可以看出，變速趨近律滑模控制的相軌跡快速收斂于原點，而常規滑模控制趨近于原點附近的抖振。

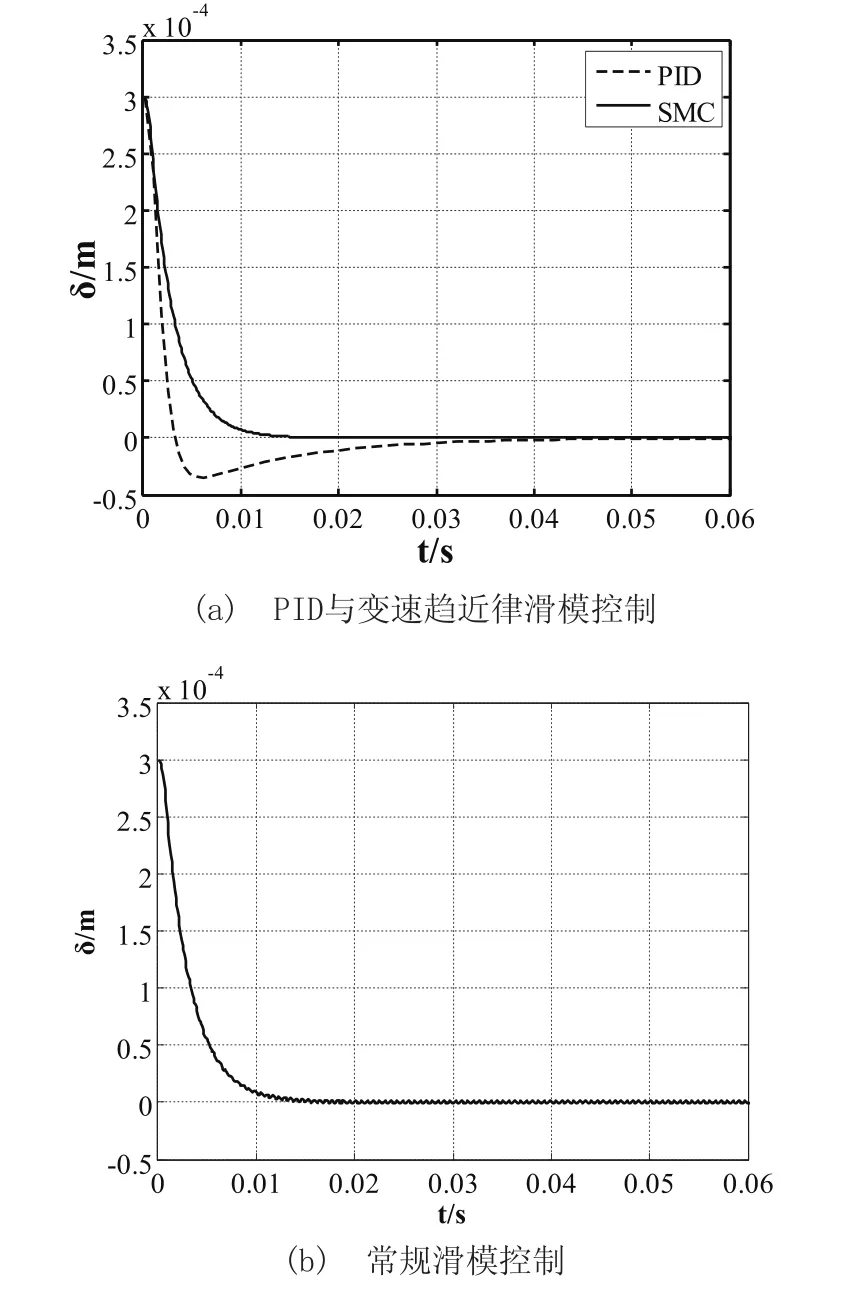
圖2 空載起浮過程位移響應

圖3 空載起浮過程控制量輸出

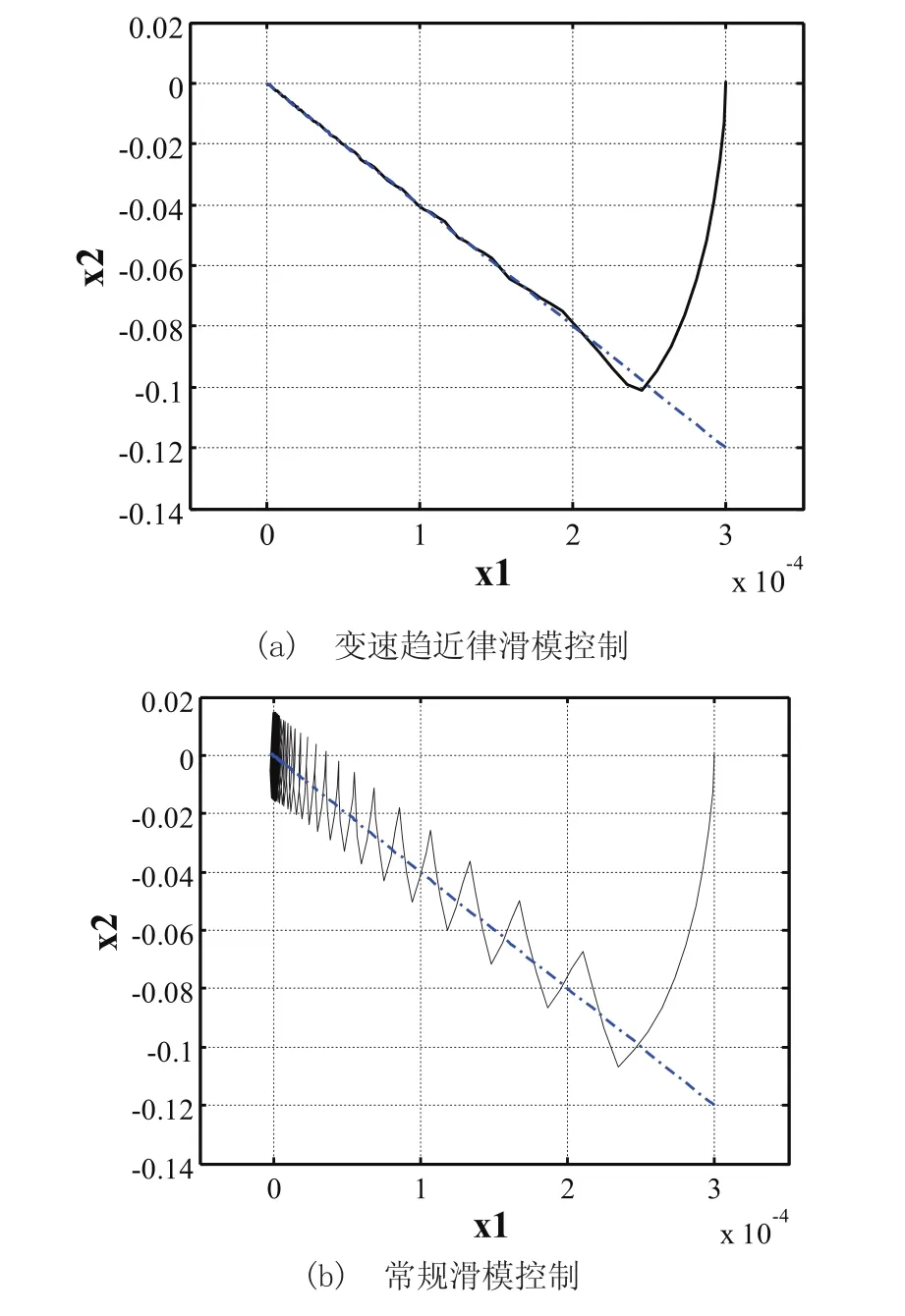
圖4 空載起浮過程相軌跡

圖5為磁懸浮系統在PID和變速趨近律滑模控制下，承載30kg負載條件下起浮過程的位移響應曲線。

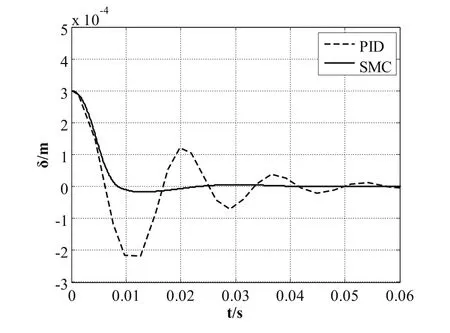
圖5 負載起浮過程位移響應

由圖5可以看出，變速趨近律滑模控制通過很好地把握位置跟蹤偏差及其動態變化趨勢，在系統參數發生很大變化的狀況下，通過強非線性的控制量輸出，使系統保證良好的動態調節特性，其魯棒性能優于PID控制。

4 結論

本文設計了一種基于指數趨近律和變速趨近律相結合的磁懸浮系統滑模控制器。在滑模運動前期采用指數趨近律，在滑模運動后期和穩定階段，采用變速趨近律，變速趨近律的符號函數增益與系統的狀態范數成比例，使該滑模控制器在提高系統的魯棒性能與降低抖振、保證穩態精度上具有良好的協調，穩態時，系統可穩定于原點。與傳統PID控制相比，該滑模控制器具有更好的動靜態性能和抗干擾能力。

[1]朱熀秋.無軸承電動機軸向磁軸承參數設計與控制系統研究[J].電工技術學報,2002,17(3):12-16.

[2]胡業發,周祖德,江征風.磁力軸承的基礎理論與應用[M].北京:機械工業出版社,2006,

[3]Ma J,Fan W J,He F H. Parameters self-adjusting fuzzy PID control in magnetic levitation system[C].2nd International Symposium on Systems and Control in Aerospace and Astronautics,2008,1:1-5.

[4]Lindlau J D,Knospe C R.Feedback linearization of an active magnetic bearing with voltage control[J].IEEE Transactions on Control Systems Technology,2002,10(1):21-31.

[5]徐龍祥,張金淼,余同正.H∞控制理論在磁懸浮軸承系統中的應用研究[J].中國機械工程,2006,17(10):1060-1064.

[6]Lee J H,Allaire P E, Tao G, Decker J A, et al. Experimental study of sliding mode control for a benchmark magnetic bearing system and artificial heart pump suspension[J].IEEE Transactions on Control Systems Technology,2003,11(1):128-138.

[7]Lin F J,Teng L T,Shieh P H. Intelligent Sliding-Mode Control Using RBFN for Magnetic Levitation System[J].IEEE Transactions on Industrial Elect ronics,2007,54(3):1752-1762.

[8]Wai R J,Lee J D.Backstepping-based levitation control design for linear magnetic levitation rail system[J].IET Control Theory & Applications, 2008,2(1):72-86.

[9]劉金琨.滑模變結構控制MATLAB仿真[M].北京:清華大學出版社,2005.

[10]姚瓊薈,黃繼起,吳漢松.變結構控制系統[M].重慶:重慶大學出版社,1997.

[11]宋立忠,姚瓊薈,蔡漢強.離散變結構系統的組合控制策略研究[J].海軍工程大學學報,2000,90(1):24-27.

Sliding mode control of magnetic levitation system based on variable rate reaching law

CHEN Wei-bing1, MAO Jing-feng2

為了抑制常規滑模控制在磁懸浮系統控制中的抖振問題，應用一種變速趨近律方法設計磁懸浮系統滑模控制器。控制器將系統的狀態范數引入滑模控制律，以自動調整變結構切換控制項的增益，控制信號抖振幅值能夠逐步衰減，并引導系統漸近穩定到原點；利用Lyapunov穩定性理論驗證了系統的穩定性，并給出了控制器參數設計的依據；仿真實驗結果表明，基于變速趨近律的磁懸浮系統滑模控制策略具有良好的動、靜態性能和較強的魯棒性。

磁懸浮系統；滑模控制；變速趨近律

陳衛兵（1966－），男，副教授，碩士，主要從事計算機工程和智能控制的教學和研究工作。

TH133；TP273

A

1009-0134(2010)06-0080-04

10.3969/j.issn.1009-0134.2010.06.28

2009-07-16

國家自然科學基金項目（60974049）；江蘇省高校自然科學研究項目（07KJD460176）；南通市應用研究項目（K2008020）；南通大學博士科研啟動基金項目（09B06）