基于粒子群優化的約束廣義預測控制實現方法

金建平

(常州機電職業技術學院，江蘇 常州213164)

廣義預測控制已經在工業過程中得到廣泛應用。在廣義預測控制中，如果被控過程是線性無約束的，并且目標函數是二次型的形式，則可求得一個解析的線性控制器，但是實際工業過程中存在著各種約束，這會使求解控制量的滾動優化問題變得復雜，通常需求解一個有約束的二次規劃或非凸規劃，而傳統的通過迭代求解二次規劃和非凸規劃方法計算量非常大，另外非凸規劃的求解對初始條件也非常敏感，這些會影響到廣義預測控制的性能。為了解決此問題，本文將粒子群優化算法應用到廣義預測控制中，解決廣義預測控制的局限性。

1 廣義預測控制算法

廣義預測控制算法是一種先進的控制算法，它廣泛應用在電力、煉油、化工和造紙等工業領域，是一種源于實際工業過程的高級控制算法，是預測控制中最具代表性的算法之一[1-4]，隨著對廣義預測控制研究的不斷深入，其理論和算法也逐步得到了完善。在廣義預測控制算法中，用受控自回歸積分滑動平均(CARMA)模型描述一個具有非平穩噪聲的實際過程可表示為：

其中，u(t)和 y(t)為過程輸入和輸出，ζ(t)為一個不相關的白噪聲序列，Δ=1-z-1為差分算子，A(z-1)、B(z-1)、C(z-1)為后移算子z-1的多項式。即：

對于單輸入單輸出(SISO)系統，假設 C(z-1)=1，則從 t時刻起，第j步后的預測輸出值可表示為：

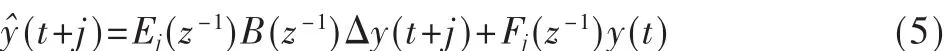
式(5)中，Ej和Fj可以通過求解丟番圖方程得到，即

式(6)中，Ej(z-1)和 Fj(z-1)是由 A(z-1)和預測長度 j唯一確定的多項式，即

令多項式Gj(z-1)=Ej(z-1)B(z-1)，整理后可得：

Gj(z-1)中前j項的系數正是對象階躍響應前j項的采樣值，記為 g1，g2，…，gj，將 Gj(z-1)展開為：

則有 gj，i=gi+1(i＜j)。因此，廣義預測控制預測模型可以寫成：

即

式(12)中：

通過長時間段預測，廣義預測控制用多步預測優化代替一步預測優化，并且優化時域隨著時間的推移而推移，具有多步預測并實施滾動優化的機制，使得系統存在時滯估計誤差或時滯變化時具有較好的魯棒性。在t時刻的優化性能指標表示為：

式(17)中：N為預測時域，Nu為控制時域，將上式極小化后得到其最優解：

最優控制量為：

式(19)中，W=[w(t+1)，…，w(t+N)]T；gT為矩陣(GTG+λI)-1GT的第1行。

式(19)中，如果控制量存在約束情況，則需求解帶有約束的二次規劃，約束非線性的存在會導致優化成為一個非凸規劃，非凸規劃的求解對初始條件非常敏感，會在局部最優解處收斂，無法保證求得的是全局最優解，本文嘗試用微粒群優化(PSO)算法來解決這一局限性。

2 PSO算法及其改進

2.1 基本PSO算法原理

由Kennedy和Eberhart提出的PSO算法[5-7]來源于對簡單社會的模擬，最初設想是模擬對鳥群覓食的過程，后來發現PSO算法是一種很好的優化工具。PSO算法與其他進化算法相類似，也是將尋優的參數組合成群體，通過對環境的適應度來將群體中的個體向更好的區域移動。與其他進化算法不同，在描述個體時，將其看成是D維尋優搜索空間的一個沒有體積的微粒(點)[8-10]，結合微粒的歷史最佳位置和群體歷史中最優微粒的最佳位置信息，按追隨最優微粒的原理，以一定的速度向目標值逼近。

設第 i個微粒的位置為 Xi=(xi1，xi2，…，xiD)，其速度為Vi=(vi1，vi2， …，viD)。 該微粒所經歷的歷史最好位置記為Pi=(pi1，pi2， … ，piD)， 也稱為Pbest， 記全體所有微粒經過的最好位置為 Pg=(gi1，gi2，…，giD)，也稱為 Pgest。 按追隨當前最優微粒的原理，對第t代的第i個微粒，PSO算法根據方程(20)和方程(21)計算第 t+1代的第 j維的速度和位置[10-11]。

式中，w為慣性權重，它使微粒保持運動慣性，使其具有擴展搜索空間的趨勢，有助于新區域的搜索、為[0，1]的隨機數；c1和 c2為加速度常數，表示將每個微粒推向Pbest和Pgest的統計加速度權重，兩者均為正值。

此外，微粒的速度vi被一個最大速度所限制。如果當前對微粒的加速導致它在某維的速度vij超過該維的最大速度 vmax，j，則該維的速度被限制為最大速度 vmax，j，使得粒子不至于因為飛行速度過高而跳過可能的優化解。

2.2 PSO算法的改進

通過對式(20)和式(21)分析發現，如果粒子群的歷史最優粒子位置Pgest在較長時間內沒有發生變化，在粒子群體快接近Pgest時，其速度更新將主要由歷史速度決定，于是速度將越來越低，粒子群呈現出強烈的“趨同性”，表現在式中的第二項和第三項接近于0。這種“趨同性”加快了算法的搜索速度，但是卻減弱了群體開拓新的搜索空間的能力。如果該最優位置為一局部最優點，則算法很容易陷入局部最優，發生早熟現象。通過粒子群優化算法的搜索機理分析發現，無論是早熟收斂還是全局收斂，微粒群中的粒子都會出現“聚集”現象。針對這個問題，本文對PSO算法作了以下改進：在微粒群從第t代向第t+1代“飛翔”時，粒子除追隨個體極值Pbest和全局極值Pgest外，還追隨從微粒群中隨機選取的某個粒子的個體極值Pn，據此改進思想，式(20)也可表示為：

式(22)中，c1為非負常數，一般取 0.5；為[0，1]的隨機數，根據仿真實驗，的取值范圍在 0～0.5之間時能獲得較好的效果；qij是隨機選取粒子的位置。在粒子的飛翔迭代公式中增加 Pn后，由 Pbest、Pgest和 Pn三者共同向下一代提供信息，使粒子獲得的信息量增大，從而可能更快地找到最優解。同時Pn的權重系數很小，相當于擾動信息，增加了粒子的多樣性，避免算法過早收斂。式(21)和式(22)組成后稱之為改進的PSO算法(MPSO)。

2.3 算法設計

引入了約束的廣義預測控制問題，實際上就是一個非線性優化問題，利用PSO算法對其進行處理的基本思想是：首先通過選擇合適的適應度函數，將有約束廣義預測控制性能指標優化的極小值問題轉化為PSO算法優化的極大值問題；然后通過空間限定法引入約束，經迭代計算后最終得到滿足約束的最優控制量求解。

基于MPSO算法的廣義預測控制結構如圖1所示，預測模型采用式(12)的形式，MPSO算法通過優化性能指標J(t)輸出控制量進行控制。

圖1 基于MPSO算法的控制結構

對優化性能指標進行變換得到適應度函數為：

式中，J(t)可以是式(18)的形式，也可以是滿足控制性能要求的其他形式，通過這種變換將GPC優化的極小值問題轉化為MPSO算法優化的極大值問題，并使MPSO算法的適應度函數值都在區間[0，1]中變化。

3 仿真實例

熱交換器是工業生產所需要的一種換熱裝置，結構如圖 2 所示，圖中，T1、T2、T3、T4、T5均為溫度控制器，F1、F2、F3均為測量流量的控制器，P1為測量壓力的控制器。系統中包括2個輸入管，即1個熱水管和1個冷水管，對應控制其流量的閥門為 V1、V2。另外還有 1個15 kW的隔熱式加熱水箱。水箱中的溫度通過冷水管中的流量來控制，而水箱中的水又經過1個離心泵，通過閥門V3來控制，輸送回熱交換器中。這其中包括很多閉環控制系統，被測量有溫度、流量、壓力等，本文選擇的閉環系統為熱交換器中循環水的溫度控制，對溫度控制回路的擾動主要有蒸汽壓力、水流速度和進水溫度。本文選取的閉環控制為圖2中的T4-V3環節。

選取系統控制量u(t)為閥門V3的位置，系統的輸出y(t)為從熱交換器到水箱的溫度T1，通過模型辨識，可以得到該系統的一階時滯的傳遞函數模型，表達式為：

設采樣時間T=4 s，將上式離散化后得：

本文嘗試用微利群優化算法來解決該非線性優化問題，從仿真結果來看，該算法具有良好的魯棒性和跟蹤性能，取得了滿意的控制效果，表明將粒子群優化算法應用到廣義預測控制中是可行和有效的。

[1]MENDES J,KENNEDY J,NEVES J.Watch the neighbor or how the swarm can learn from its environment[C].Proc.Of the IEEE Swarm Intelligence Symposium.Indiana:IEEE Press,2003：88-94.

[2]CLARKE D W.Generalized predictive control-part I[J].Automatica,1987,23(2):137-148.

[3]CLARKE D W.Generalized predictive control-part II extensions and interpretations[J].Automatica,1987,23(2):149-160.

[4]王偉.廣義預測控制理論及其應用[M].北京:科學出版社,1998.

[5]KENNEDY J,EBERHART R.Particle swarm optimization[C].Proc.IEEE Int.Conf.on Neural Networks.Perth:IEEE Press,1995：1942-948.

[6]SHI Yu Hui,EBERHART R.A modified particle swarm optimizer[C].Proc.IEEE Int.Conf.on Evolutionary Computation.Anchorage:IEEE Press,1997：303-308.

[7]ZHANG L P,YU H J,HU S X.A new approach to improve particle swarm optimization[C].Proc.Of the Genetic and Evolutionary Computation Conf.Chicago:IEEE Press,2003：134-142.

[8]MILLONAS M M.Swarms phase transition and collective intelligence[M].MA:Addison Wesley,1994.

[9]SHI Y，EBERHART R C.Fuzzy adaptive particle swarm optimization[C].Proc.Of the IEEE Congress on Evolutionary computation.Seoul,Korea:IEEE Press,2001：101-106.

[10]RATNAWEERA A,HALGAMUGE SK,WATSON C.Selforganizing hierarchical particle swarm optimizer with timevarying acceleration coefficient[C].IEEE Trans.Evolutionary computation.IEEE Press,2004：240-255.