基于加權有向圖的權頻繁模式挖掘算法
封 軍,鄭 誠,鄭小波,肖 云
(安徽大學 計算智能與信號處理教育部重點實驗室,安徽 合肥230039)
在現實世界中,許多復雜問題可以被描述成有向圖及在其上的遍歷問題,其中具有代表性的實例是WWW的站點訪問[1],可以把每個網站站點模擬成一個有向圖,圖中的頂點代表Web頁面,并代表一個頁面到另一個頁面的鏈接,用戶在網站上訪問的頁面記錄可以看成在一張圖上的遍歷,一旦所有的遍歷都給出,即可從中挖掘出有用的信息知識。這些信息知識的表現之一就是頻繁模式的挖掘發現。而通過這些頻繁模式的發現,不僅可以改進網站系統的性能,而且還可以相應地制定出市場決策(例如在用戶經常訪問的Web頁面做產品推銷和廣告發布等)。此外,如超文本訪問、人際關系網絡構成等,都可以通過圖來模擬其基本特征。所以,圖遍歷模式挖掘一直是一個研究熱點。
針對帶權值的有向圖的挖掘已不再有效,例如Apriori、FP-增長算法等[4]傳統挖掘算法。本文為了解決加權有向圖遍歷挖掘的問題,提出一種基于有向加權圖權頻繁模式挖掘算法,簡稱GTWF算法。對于加權圖遍歷模式的挖掘,傳統的圖挖掘沒有考慮到帶有權值的圖遍歷模式挖掘[5],對于此項研究,先前的工作大多是與挖掘加權關聯規則和其子問題——加權頻繁項集有關的,而沒有考慮到帶有權值的圖遍歷問題。
1 基本概念
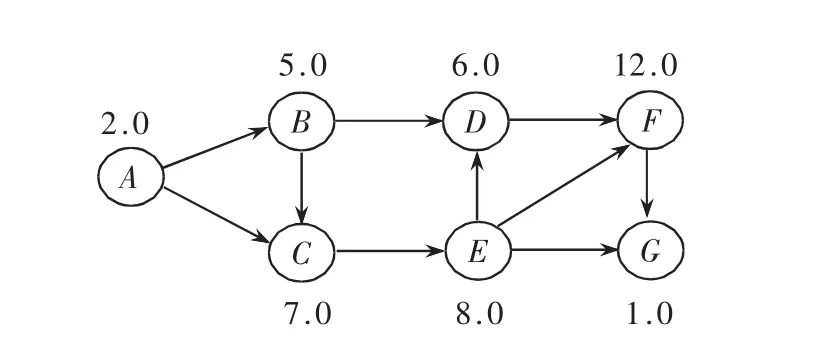
圖1 加權有向圖
定義1加權有向圖:給某個有向圖的每個頂點加上相應權值,這些權值各自代表相應頂點的重要程度,這樣的圖稱作加權有向圖。
例如圖1,如果把這個有向圖看作一個Web站點的結構圖,則它有 7個結點{A,B,C,D,E,F,G},每個頂點分別代表一個網頁,還有9個邊,他們代表兩網頁之間的鏈接,并且在每個結點有一個相應的權值,這個權值可以代表用戶對這些Web頁面的興趣度[6],這樣的權值可根據用戶在Web頁面上的停留時間、用戶對Web頁面訪問行為[2](網頁滾動條的次數、被收藏的次數等)或訪問Web頁面的用戶數進行分析和評估得出。
定義2路徑遍歷數據庫(Path Traversal Database),如表1,把所有關于有向圖上的遍歷路徑綜合到一個數據庫D中,這個的數據庫稱為路徑遍歷數據庫。例如,用戶對某一Web站點訪問時,把他們各自訪問所有Web頁面按訪問的先后順序進行排列后,得到一系列訪問路徑,這樣的路徑稱為在站點結構圖上的遍歷路徑。如路徑遍歷模式P:<B,C,E,F>,即為圖1中的一個遍歷路徑。
定義3支持度,把某一遍歷路徑模式P在上述數據庫D中出現的次數記為count(P),稱為P的支持數。關于上述數據庫D,設|D|為所有遍歷路徑的總數。所以P的支持度可以如下定義:

表1 路徑遍歷數據庫D

定義4可擴展模式[3],若一個模式P擴展為長度更長的模式后,有可能成為頻繁模式,則稱模式P為可擴展模式。如果判斷一個模式P是否具有可擴展性,則P要滿足下述情況,給定一個最小支持數 minsup,若 k-模式 P要擴展到 k+1模式,必須滿足 count(P)>=minsup,則稱模式P具有可擴展的可行性(Feasible)。例如,設定最小支持數 minsup=2,有 2-模式 P:<A,B>,從上述訪問路徑數據庫 D中得出 count(P)=2,然后可得 count(P)>=minsup,則 P具有擴展 3-模式<A,B,C>或<A,B,D>的可行性。
定義5權支持度[3](weighted support),如模式P的權支持度(wsupport)可定義如下:
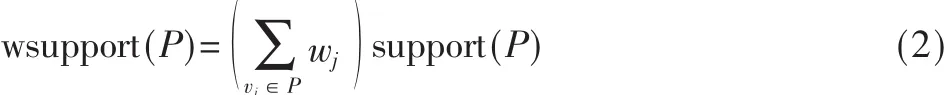
這里 V={v1,v2,...,vn}為圖的頂點集合,每一個頂點 vj有一個權 wj≥0,wj∈W,W={w1,w2,...,wn}。
定義6權頻繁模式[3],如果 P為權頻繁模式,則 P的權支持度(wsupport)一定要大于或等于給定的一個最小權支持度(minwsup)。數學表達式如下:

所以根據式(1)、式(2)和式(3),如P是權頻繁項,可以得到以下的不等式:

把式(4)右邊進行向上取整,得到的值定義為P支持數的較低限度(lower bound),簡稱為sbound(P)。如式(5):
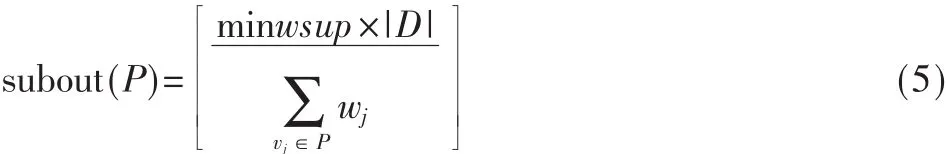
最終,綜合式(4)式和式(5),可以得到以下定義,當count(P)≥sbound(P)時,模式 P為權頻繁模式。
2 基于加權有向圖的權頻繁模式挖掘算法
本文提出的基于加權有向圖的權頻繁模式挖掘算法(簡稱GTWF算法)過程與傳統 Apriori算法基本相似,最主要的過程是剪枝步和候選項的產生,不同的是GTWF算法提出模式的可擴展性的概念,并把它應用到剪枝和候選項產生操作中,這樣可以找出可能具有權頻模式的所有模式。下面,對GTWF算法的過程進行詳細描述。
2.1 剪枝步
在本文算法中,剪枝操作主要是把沒有可能成為權頻繁模式的候選項剪掉,保留那些有可能成為權頻繁模式的候選項。由定義4可知,如果模式P滿足條件count(P)≥minsup,則它具有可擴展性,否則 P從候選模式集中剪掉。
結合定義4可得出下列算法:

2.2 候選項的產生
本文算法的候選項主要是從可擴展模式集中產生的,如果一個可擴展 k-模式<p1,p2,…,pk>的兩個(k-1)-子模式<p1,p2,…,pk-1>和<p2,p3,…,pk>都是可擴展的,則它們之間有完全向下閉合性。當存在完全向下閉合性時,則可以從可擴展的k-模式集Ck產生一個候選(k+1)-模式集Ck+1,算法描述如下:

2.3 基于有向加權圖權的頻繁模式挖掘算法(GTWF算法)步驟
GTWF算法的主要過程與Apriori算法基本相似,就是把剪枝操作算法與候選模式產生算法結合在一起。下面是GTWF算法的詳細步驟:

2.4 實例分析
通過圖1和表1數據做GTWF算法相應的實例分析。假設最小權支持度minwsup=5,最小支持數minsup=2。下面根據GTWF算法步驟做具體實例分析。
(1)根據算法步驟 1,掃描路徑遍歷數據庫 D,得出權頻繁模式的最大可能長度u=4,總的數據庫記錄數|D|=8。
(2)根據算法步驟2,初始化長度為1的候選模式如下:
C1={<A>,<B>,<C>,<D>,<E>,<F>,<G>}
(3)表 2、表 3、表 4和表 5是根據算法步驟 3、步驟4、步驟5循環執行所得出的結果。
得出最終的權頻繁模式集為:{<C,E>,<B,C,E>}。
3 實驗分析
本實驗是在 Pentium4 3.0 GHz,內存為1GB的PC上進行,算法的實現環境為VC++6.0和SQL Server 2005。實驗數據是合成數據,實驗數據中加權圖的頂點數(v)最多有500個,頂點權值(w)范圍為 0<w≤12。合成路徑遍歷數據庫|D|=10 000,最小權支持度(minwsup)可分別為1,2,3,4,5。最小支持數(m)可分別為 2,3,4,5。
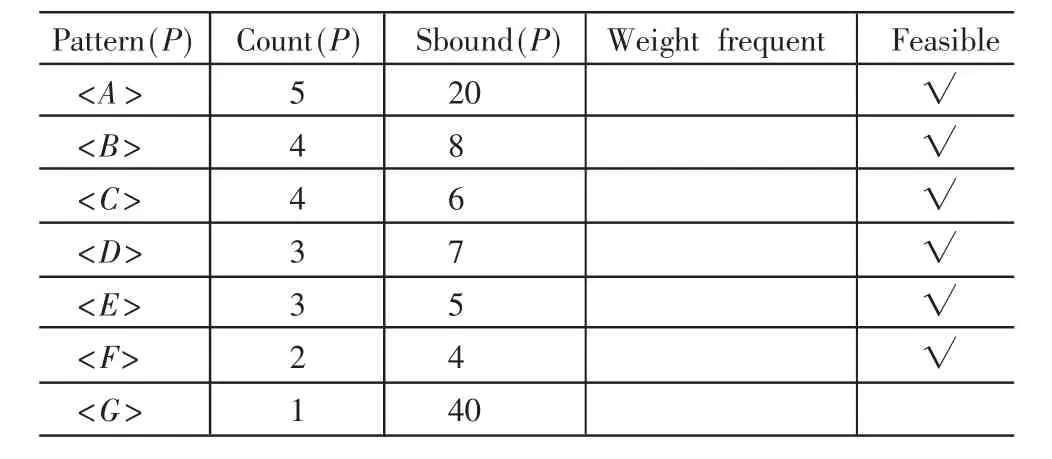
表2 一項模式集
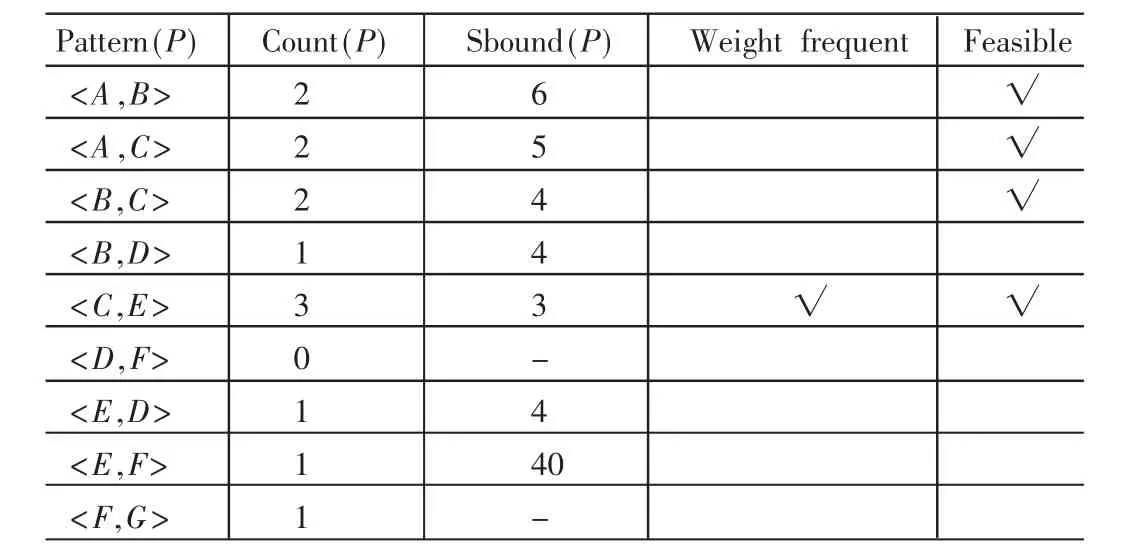
表3 二項模式集
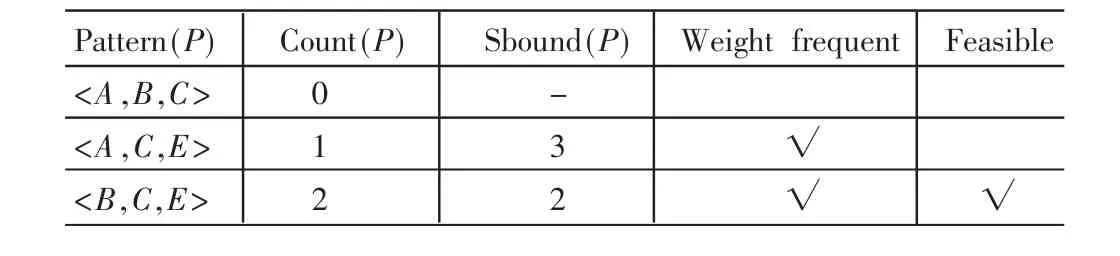
表4 三項模式集

表5 四項模式集
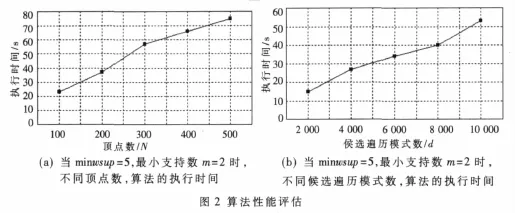
實驗研究了不同的最小支持數閾值、最小權支持度閾值、候選遍歷模式數、圖的頂點數與運行時間的關系。圖2、圖3分別進行算法性能評估。圖2(a)主要說明不同頂點數與執行時間的關系——隨著圖頂點數的增加,算法執行時間也是遞增的。圖2(b)主要說明候選遍歷模式數與執行時間的關系——隨著候選遍歷模式數目的增加,執行時間也是呈遞增狀態。圖3隨著最小支持數(m)的增加,執行時間將減少,因為當最小支持數增加時,可擴展模式數就越來越少,相應的剪枝等操作也少了,所以執行時間就變少。另外圖中還說明隨著最小權支持度(minwsup)的增加,執行時間也減少,因為隨著最小權支持度的增加,從算法循環一開始,可確定的權頻繁模式就減少,直接導致可供下次循環的候選模式也減少了,從而減少了搜索和剪枝等操作,所以執行時間就減少。
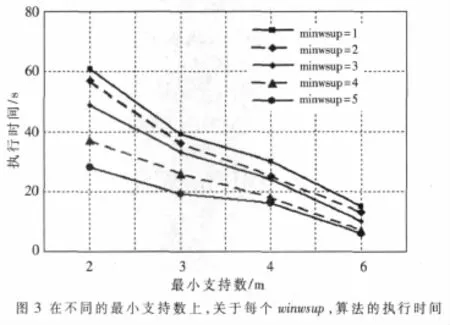
本文主要分析討論了通過加權有向圖的遍歷來挖掘權頻繁模式的問題,提出了解決此問題的GTWF算法。在算法中,利用權支持度、可擴展模式和權頻繁模式等概念,并通過剪枝操作和候選模式產生操作來實現算法對圖遍歷模式的挖掘,最后通過實驗對算法的性能進行了驗證。實驗結果表明算法在可伸縮性與執行性能等方面具有較好的效果。
[1]HEYDARI M,HELAL R A,GHAUTH K I.A graphbased Web usage mining method considering client side data[C].2009 IEEE.
[2]TAO Yu Hui,HONG Tzung Pei,SU Yu Ming.Web usage mining with intentional browsing Data[C].2007 Elsevier Ltd.
[3]LEE S D,PARK H C.Mining weighted frequent patterns from path traversals on weighted graph[C].Department of Computer Engineering,Korea Maritime University,Korea
[4]張云濤,龔玲.數據挖掘——原理與技術[M].北京:機械工業出版社,2004.
[5]韓家煒,KAMBER M.數據挖掘:概念與技術[M].北京:機械工業出版社,2001:351-364.
[6]郭巖,白碩,楊志峰,等.網絡日志規模分析和用戶興趣挖掘[J].計算機學報,2005,28(9):1483-1496.

