多傳感器狀態融合估計在雷達跟蹤中的應用
李雄杰
(浙江工商職業技術學院 機電工程系,浙江 寧波 315012)
隨著科學技術的發展,特別是微電子技術、集成電路技術、計算機技術、信號處理技術及傳感器技術的發展,多傳感器信息融合已經發展成為一個新的研究領域,并在軍用領域和民用領域均得到了廣泛應用。
多傳感器信息融合的基本原理如同人腦綜合處理信息的過程,即充分利用多個傳感器資源,通過對各種傳感器及其觀測信息的合理支配與使用,將各種傳感器在空間和時間上的互補與冗余信息依據某種優化準則組合起來,從而得出更為準確、可靠的結論。
現代戰爭的多樣性和復雜性提出了對信息處理更高的要求,信息融合可對多傳感器提供的多種觀測信息進行優化綜合處理,從而獲取目標狀態、識別目標屬性、分析目標意圖與行為,為電子對抗、精確制導等提供作戰信息。本文將基于Kalman濾波的多傳感器狀態融合估計方法應用到雷達跟蹤系統。仿真實驗表明,三個傳感器融合所獲得的估計值都更加貼近于目標信號,因而提高了對雷達系統的跟蹤精度。
1 卡爾曼濾波器
多傳感信息融合的主要任務之一就是利用多傳感器信息進行目標的狀態估計。目前,進行狀態估計的方法很多,Kalman濾波器是一種常用方法。Kalman濾波器在機動目標跟蹤中具有良好的性能,它是最佳估計并能夠進行遞推計算,即它只需要當前的一個測量值和前一個采樣周期的預測值就能進行狀態估計。
考慮一個離散時間的動態系統,它有如下形式:

其中,x(k)∈Rn×1表示系統在離散時間 k的狀態向量,A(k)∈Rn×n是狀態轉移矩陣 ,z(k)∈Rq×1(q≤n)表示傳感器的觀測向量 ,C(k)∈Rq×n是觀測矩陣 。 w(k)∈Rn×1和v(k)∈Rq×1分別是系統噪聲和觀測噪聲序列,一般假設是高斯白噪聲,其協方差分別為Q(k)和R(k)。
針對動態系統(1)和(2),Kalman遞推濾波算法[1]如下:
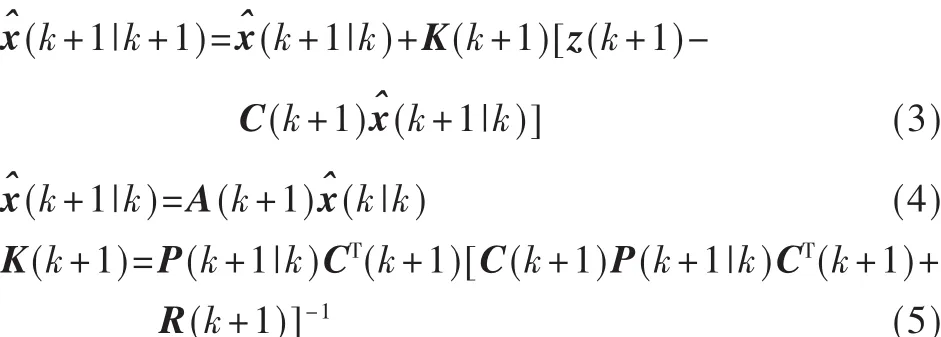
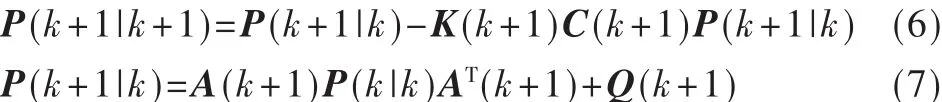
2 多傳感狀態融合估計算法
單采樣率多傳感器狀態融合估計的研究方法主要有基于概率論的方法、基于Kalman濾波的方法、基于推理網絡的方法、基于模糊理論的方法、基于神經網絡的方法,以及基于小波、熵、類論、隨機集、生物學靈感、Choquet積分的方法等等[2]。基于Kalman濾波的方法由于具有操作簡單、計算量小、實時性強等優點,得到最為廣泛的研究。
下面重點介紹基于Kalman濾波的分布式數據融合狀態估計算法。設多傳感器系統有如下形式[3]:

其中 ,x(k)∈Rn×1表示系統狀態向量 ,A(k)∈Rn×n是轉移矩陣,z(i,k)∈Rqi×1(qi≤n)表示第 i個傳感器的觀測向量 ,C(i,k)∈Rqi×n是觀測矩陣 。 w(k)∈Rn×1和 v(i,k)∈Rqi×1分別是系統噪聲和觀測噪聲序列。
狀態向量初始值x(0)為一隨機向量,并且有:

假設 x(0)、w(k)和 v(i,k)之間是統計獨立的 ,i=1,2,…,N表示傳感器。數據融合的目的是通過合理利用這些傳感器的觀測信息,獲得狀態的最優估計值。
Carlson在1990年提出了一種最優數據融合準則[4]。設x^i(k|k)和Pi(k|k)分別表示狀態基于傳感器i觀測信息的Kalman濾波估計值和相應的估計誤差協方差陣,對于 i=1,2,…,N,假設x^i(k|k)互不相關,則最優聯邦濾波器最優數據融合準則由下式給出:

其中,
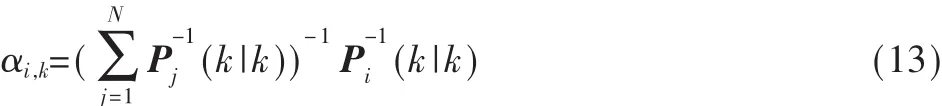
相應的估計誤差協方差矩陣為

可以證明:

基于第i個傳感器信息的Kalman濾波估計器如圖1所示。Carlson聯邦融合估計算法流程圖如圖2所示。
3 雷達跟蹤系統仿真
考慮具有3個傳感器的雷達跟蹤常加速度模型[5],其離散狀態方程為:
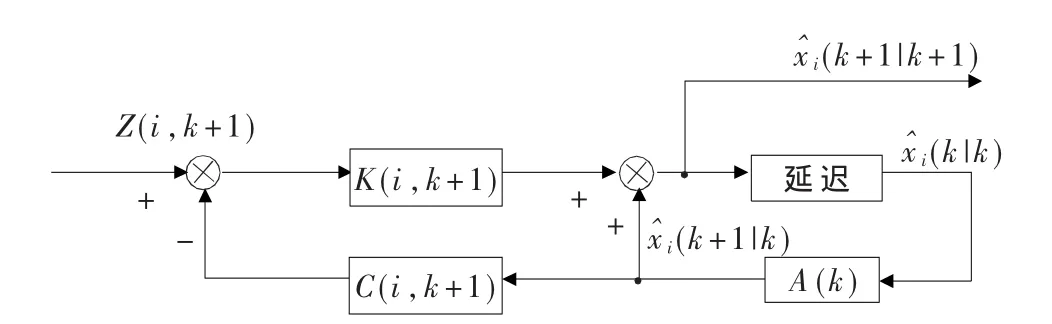
圖1 Kalman濾波方框圖
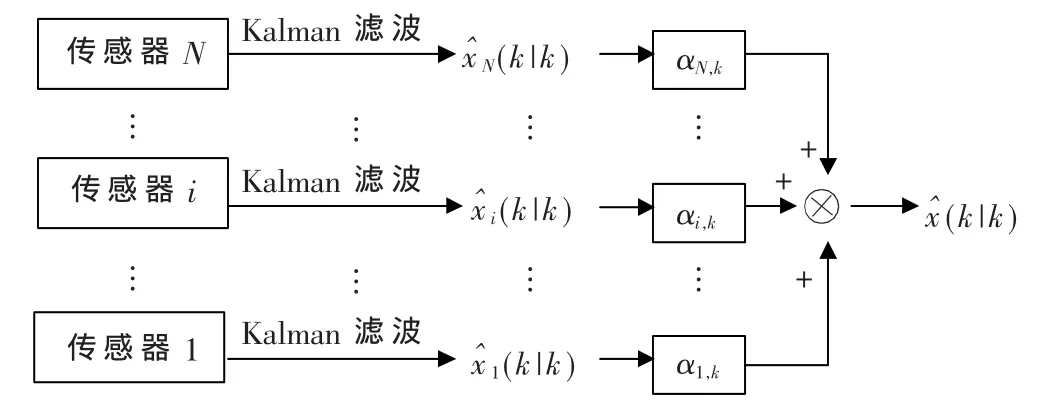
圖2 聯邦融合估計算法流程圖
設傳感器的采樣點數為600,則10次Monte Carlo仿真的統計結果如表1所示。表1給出了估計誤差絕對值均值比較,3個傳感器融合的綜合估計誤差是最小的。
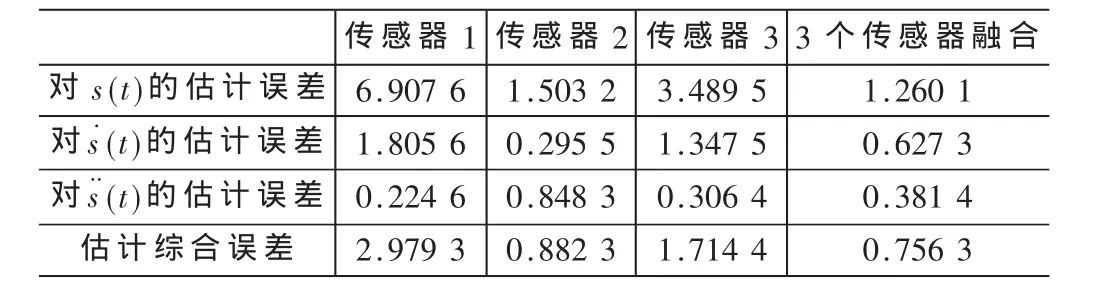
表1 估計誤差絕對值均值比較
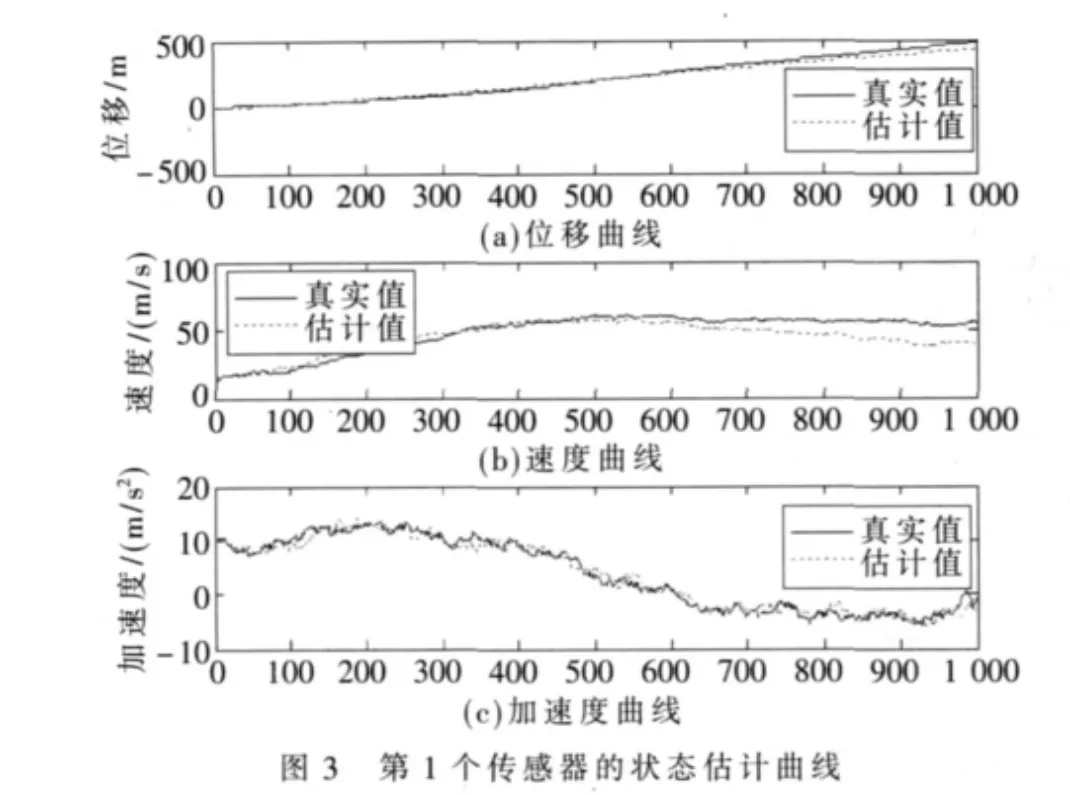
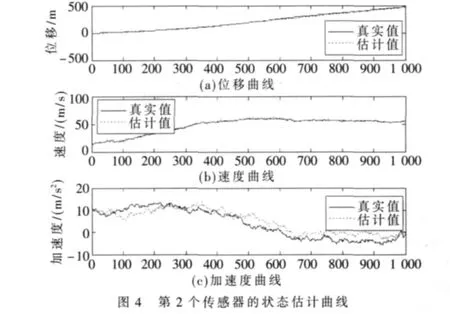
第1個傳感器、第2個傳感器、第3個傳感器及3個傳感器融合的狀態估計曲線分別如圖 3、圖4、圖5、圖6所示。圖中橫軸為仿真步數,每步時間為0.01 s。若仔細觀察這些狀態估計曲線,則單傳感器狀態估計曲線均有不足,如圖3對速度跟蹤不是很好,圖4對加速度跟蹤不是很好,圖5對速度跟蹤也不是很好,只有圖6對位移、速度及加速度跟蹤均較好。由此可見,與單傳感器Kalman濾波的結果相比,3個傳感器融合所獲得的估計值都更加貼近于目標信號,從而證明了本文算法的有效性。


信息融合技術具有提高系統的可靠性和穩定性等優點,狀態融合估計是其中研究熱點之一。本文將基于Kalman濾波的多傳感器狀態融合估計方法應用到雷達跟蹤系統,仿真實驗表明,融合3個傳感器的信息所獲得的狀態估計誤差小于利用任何單傳感器進行Kalman濾波得出的狀態估計誤差,因而本方法對雷達系統的跟蹤是很有效的。本方法可推廣用于組合導航、信號處理、圖像處理、故障檢測與容錯等應用領域。
[1]陳新海.最佳估計理論[M].北京:北京航空學院出版社,1987.
[2]潘泉,于昕,程詠梅,等.信息融合理論的基本方法與進展[J].自動化學報,2003,29(4):599-615.
[3]YAN L P, LIU B S, ZHOU D H.The modeling and estimation of asynchronous multirate multisensor dynamic systems, Aerospace Science and Technology, 2006,10(1):63-71.
[4]CARLSON N A.Federated square root filter for decentralized parallel processors[J].IEEE Transactions on Aerospace and Electronic Systems, 1990,26(3):517-525.
[5]SUN S L.Multi-sensor optimal information fusion Kalman filters with applications[J].Aerospace Science and Technology, 2004,8(1):57-62.

