一種新穎的概率仿真優化方法

蔡奎生

（蘇州經貿職業技術學院，江蘇 蘇州 215000）

仿真優化就是在現代先進優化理論的基礎上，采用計算機仿真技術來獲得待研究系統的一種較為優化的決策[1]。仿真優化已廣泛地應用到各個領域，如自動控制、系統設計和仿真算法優化等[2～4]。 目前較為常用的仿真優化方法有[5～8]：隨機優化方法、基于梯度的方法、響應曲面法及智能優化方法。這些仿真優化方法已被廣泛地應用于諸多領域，如生產制造系統[9]、經濟系統[10]。

1 概率仿真優化方法

1.1 仿真重復次數的確定方法

對于大多數實際的仿真優化問題來講，點xk處的響應值不等同于它的適應度值F(xk)，所以需要在點xk處進行多次仿真。在本文中，假設在點xk處進行p次仿真試驗，則多次仿真取平均值的計算方式如下：

這里，筆者采用以下方式來確定p的取值：

其中，pi表示在試驗點Xi處需要進行重復仿真試驗的次數，m表示一個固定的參數，||·||表示計算向量的模，Xi表示第i個個體，X*表示當前種群中的最優個體。

1.2 兩個個體的優劣比較

在公式(1)中，除非p的取值非常接近于正無窮，否則使用R(xk)來替代f(xk,w)都是不合適的。所以，很難采用一種精確的方法來比較R(xk)和R(xk+1)。筆者采用假設檢驗方法來嘗試構造判斷兩個個體優劣的方法。可構造以下假設：

其中，R(x1)和R(xw)分別表示點x1和 x2處所得到的平均響應值，μ1和μ2分別表示點x1和x2處的實際適應值。這樣就可在給定檢驗水平α下基于統計量R(x1)和R(x2)來對上述假設檢驗做出判斷。如果上述假設被拒絕，則μ1＜μ2，說明染色體以1-α的置信水平水平優于染色體x1。

1.3 多個個體的優劣排序

設X1,X2,…,Xn分別表示當前種群中的n個個體；μ1,μ2…,μn分別表示這 n個個體的實際應值；R(x1),Rx2),…,R(xn)分別表示這n個個體的平均適應值。這里，可采用下面的思路來對n個個體的進行排序：先找出所有n個個體中實際適應度值最大的那個個體(具體方法參見1.2節)，從原隊列中去掉該個體，將該個體排在新隊列中的首位；依次類推，直到原來隊列中的個體數目為零時排序結束。

2 量化正交遺傳算法

本文定義染色體x=(x1,x2,…,XN)的成本為f(x)。全局優化問題等價于找到成本最小的染色體。

2.1 初始種群的生成

在求解全局優化問題前，我們不知道全局優化點位于哪個區域。因而就希望優化算法從一開始就在可行解空間中進行均勻地、離散地搜索，以至于算法可以均勻地搜索整個可行解空間。不難發現，正交表在所有可能的組合中指定了均勻離散分布的數量規模比較小的組合群。所以，正交設計方法是能產生一組比較好的初始種群的潛在的方法。定義第i個自變量為xi，因而每個染色體有N個自變量。這些自變量都是連續的，但正交設計方法僅僅針對于處理那些離散的自變量。為了克服這個缺點，我們將每個自變量都量化成有限的值。本文將自變量xi的定義域[li,ui]量化成Q1個水平ai1,ai2,…aiQ1，這里的Qa是奇數，具體的aij計算公式如下：

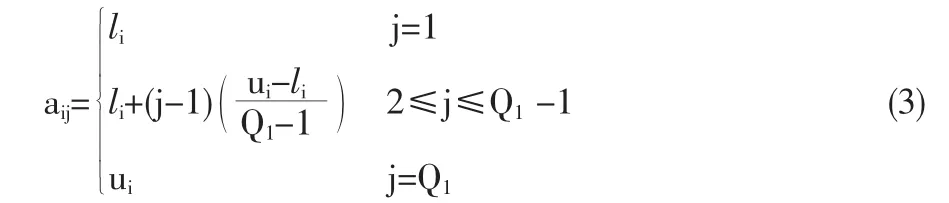
為方便起見，稱aij為第i個自變量的第j個水平，定義ai=(ai1,ai2,…,a1Q1)。完成自變量的量化操作以后，自變量x1擁有Q1個可能水平ai1,ai2,…,aiQ1，然后可行解空間包含個點。本文采用正交設計的方法在可行解空間中選擇一小群樣本點。

首先構建一個合適的正交表。如前所述，前面的構造正交表的方法僅能構造正交表LM1()，此處的M1=，J1是滿足以下條件的正整數：

當可行解空間比較大時，這種方法很可能生成收斂性比較好的初始點。然而，M1值的大小依賴于N和Q1的大小，不能任意地增大。為了解決這個問題，將可行解空間分解成S個部分，這里的S是一個設計參數。將s維區間[l,u]分解成為以下 S 個部分：[l(1),u(1)]，[l(2),u(2)]，…，[l(s),u(s)]，這里

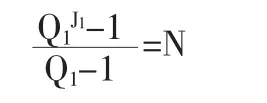
由于優化問題的維數N是給定的，因而可能不存在滿足上式的Q1和J1。我們可以將上面的要求放寬一些，選擇滿足下列條件的最小的正整數J1：

其中，i=1，2，…，S；ls是諸如第 s個元素為 1 其他元素為0的一個N維向量。我們應用正交表LM1()在每一個部分都生成M1個染色體，這樣我們總共就得到了M1S個潛在的染色體。我們從中選擇G個代價最小的初始種群染色體。

2.2 量化的正交交叉算子

量化正交交叉算法將父代個體定義的求解空間量化成有限數目點，然后應用正交設計方法選擇一群有代表性的規模比較小的潛在子代個體。考慮以下兩個父代個體：

將每一個父代求解空間[lparent,upaent]量化成Q2份，這樣任意兩個連續水平之間的差異是相同的。尤其值得一提的是，我們將第 i維區間量化成 βi1,βi2,，βiQ2，其中：

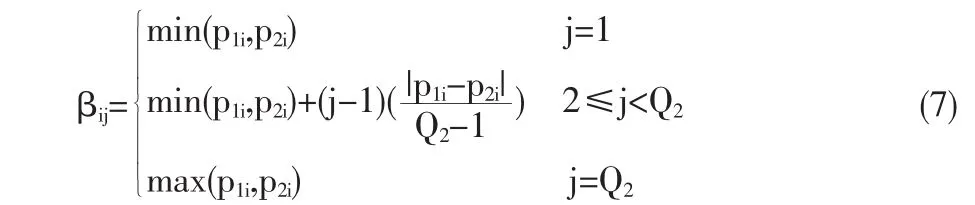
定義 βi=(βi1,βi2,…,βiQ2)。 由于種群的不斷進化和改進，種群成員之間越來越接近，兩個父代個體定義的求解空間也越來越小。由于Q2是定值，隨著量化點的逐步接近，我們就可以得到越來越精確的結果。

在完成求解空間[lparent,upaent]的量化后，應用正交設計方法選擇一批數據規模比較小的富有代表性的樣本點作為潛在的子代，然后選擇一些代價最小的樣本點作為子代。為了避免在選擇過程中大規模的評價種群點，每一對父代盡可能不要產生太多的潛在子代點。基于這個目的，將變量x1,x2,…,xN分成F組，這里的F是一個很小的設計參數。每一組將會被看成一個因素。這樣，相應正交表的組合數目將會減少，然后就產生一個規模比較小的初始種群。這里，隨機地生成F-1個整數 k1,k2，…,kF-1這里不妨假定 1＜k1＜k2＜…＜kF-1。 然后對于每個染色體x=(x1,x2,…,xN)產生以下F個因素。

因為x1,x2,…,xN可以被量化，我們為第i個因素定義如下Q2各水平：

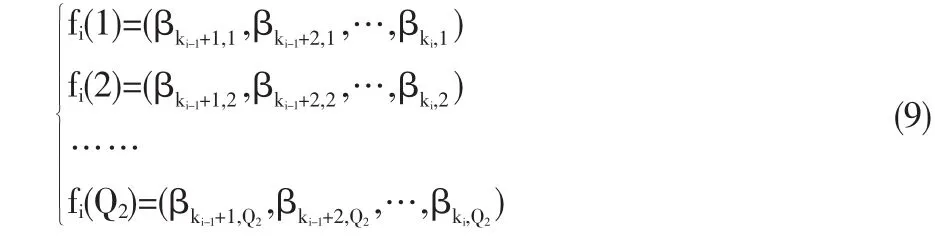
3 二級分銷網絡系統仿真模型

對于一個確定了分銷中心的二級分銷網絡系統，可以把其看成是一個在分銷中心產生庫存的庫存系統。這個庫存系統以分銷中心為中心，集成考慮庫存和運輸。通過控制庫存可以實現對整個分銷網絡進行管理。離散事件系統仿真能夠準確記錄系統各個環節的狀態變化情況，并能根據這些記錄得到系統的各個評價指標的統計結果。

3.1 目標和邊界

應用仿真技術研究二級分銷網絡系統的目的是通過各種庫存指標比較各種訂貨策略的優劣，如在不同的需求情況下，何時訂貨、訂多少貨為宜，庫存安全量如何確定等。二級分銷網絡系統的優劣常采用“費用(效益)”的高低來衡量，主要的費用有運輸費用、訂貨費用、倉儲費用和缺貨損失費等。在整個分銷系統的不斷變化中，引發事件是用戶需求的產生和滿足，因此把用戶需求的產生和滿足作為模型的邊界。

3.2 實體

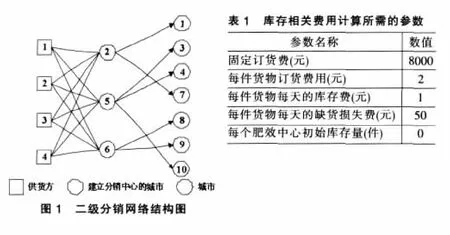
二級分銷網絡系統的實體包括供貨方、分銷中心、用戶和貨物。其中，供貨方、分銷中心和用戶為永久實體，貨物為臨時實體。對于供貨方來說，必須滿足供應量足夠，即不管訂貨需求何時到達，供貨方都能滿足分銷中心的訂貨需求；對于用戶來說，需求的產生是無條件的，只是在時間上符合某種規律，而與其它因素無關。

3.3 流程分析

在二級分銷網絡系統中，分銷中心庫存量的變化是由用戶需求和分銷中心訂貨兩個方面的因素引起的。由于用戶需求使得庫存量不斷減少，為了保證供應，就需要訂貨來補充庫存量。隨著需求和訂貨的不斷發生，庫存量呈現動態分布。

3.4 仿真算法

本文采用事件調度法對二級分銷網絡系統進行仿真。事件是指狀態變化的瞬間。事件調度方法以事件為基礎，用事件的觀點來分析現實系統，它通過定義事件及每個事件的發生對系統狀態的影響，按時間順序確定并執行每個事件發生時有關的邏輯、數學關系。基于事件調度的仿真模型用于描述各類離散事件的發生及相關聯的邏輯變換。

在用事件調度法建立模型時，全部事件都放在事件鏈表中。由時間控制模塊從事件鏈表中選擇具有最早發生時間的事件，并將仿真時鐘修改到該事件發生的時刻，再調用與該事件相應的事件處理模塊和動畫圖像描繪模塊，這樣，事件的選擇與處理不斷地進行，直到仿真終止條件得到滿足或終止事件發生為止。

4 實證分析

某公司已經對分銷網絡進行了設計，如圖1所示。本部分通過分析歷史數據得到用戶需求產生的時間分布的基礎上，通過系統仿真從而得到最優的訂貨策略。

4.1 基本設置

筆者采用Arena軟件自帶的Input Analyzer功能對歷史數據進行分析，得到用戶的需求達到的時間間隔服從參數為λ(λ1=42,λ3=45,λ4=22,λ7=60,λ8=55,λ9=26,λ10=39)的泊松分布。通過分析，確定計算庫存相關費用所需的參數如表1所示。

筆者采用定期定量訂貨方式，三個分銷中心分別采用每周訂貨1000件或5000件。仿真系統模擬所有的8種組合，從中選取最優的訂貨策略。編號為2、5、6的分銷中心分別按照自己的訂貨策略發出自己的訂單，然后比較與編號為1、2、3、4的供貨方的距離，從中選擇距離最近的供貨方供貨。為了計算方便，這里假設供貨方的供應量不受限制。記錄其中產生的訂貨費、運輸費和庫存量增加。編號為1、3、4、7、8、9、10的用戶按照相應的泊松分布產生自己的需求，分別把訂單發給相應的分銷中心。若分銷中心可以滿足訂單所需貨量則發貨，否則產生缺貨。記錄其中發生的運輸費用、倉儲費用和缺貨損失費用。

4.2 實驗結果

仿真時間設為1年，仿真得到各種訂貨策略下的費用見表2。在表2中，用“1”表示采用每周訂貨1000件的訂貨策略，用“2”表示每月訂貨5000件的訂貨策略。例如：表2中最后一行的訂貨策略為分銷中心2每月訂貨5000件，分銷中心5每周訂貨1000件，分銷中心6每月訂貨5000件。

通過比較，可以得到使這個二級分銷網絡系統總費用最少的訂貨策略為:分銷中心2每周訂貨1000件，分銷中心5每月訂貨5000件，分銷中心6每月訂貨5000件，其費用為27415436元。

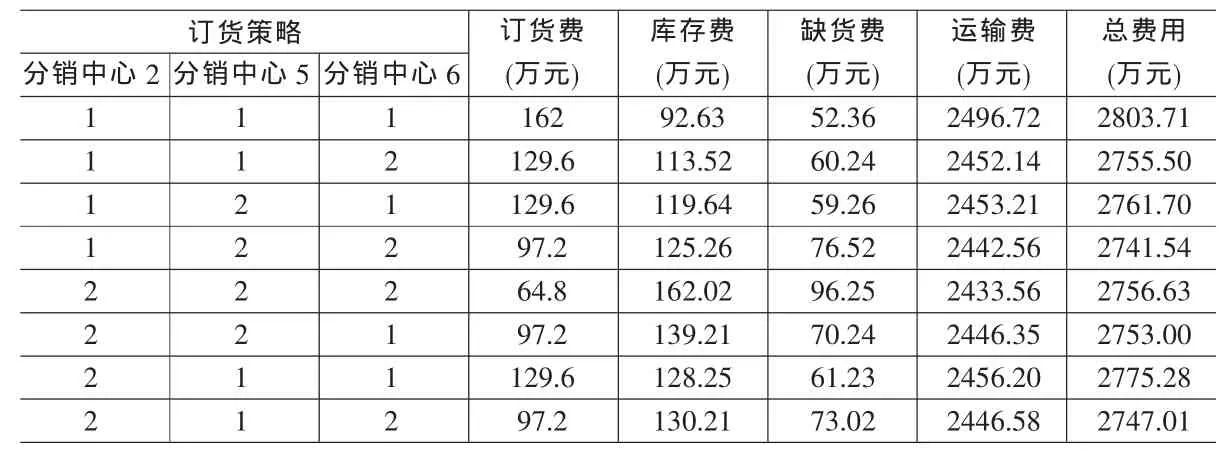
表2 各種訂貨策略下的費用表

5 結束語

本文的主要創新點是：提出了一種將計算機仿真技術、遺傳算法和假設檢驗等完美地結合的概率仿真優化方法。在二級分銷網絡系統的實證研究表明，采用本文方法能獲得比較滿意的優化結果。

[1]Cao X R,Ho X C.Estimation of Co-Join Time Sensitivity in Queuing Networks Using Perturbation Analysis[J].Journal of Optimization Theory and Applications,1997,44(3).

[2]Olsder G J.On the Characteristics Equation and Minimal Realizations for Discrete-Event Dynamic System[J].Analysis and Optimization of Systems,1998,83.

[3]Azadivar,F.A Tutorial on Simulation Optimization[C].In Proceedings of the 1992 Winter Simulation Conference,1992.

[4]Fu,M.C.Optimization Via Simulation:A Review[J].Annals of Operational Research,1994,(53).

[5]Rosenblatt,M.J.,Roll,Y.,Zyse,V.A Combined Optimization and Simulation Approach for Designing Automated Storage/Retrieval Systems[J].IIE Transactions,1993,25(1).

[6]Kleijnen,J.P.C.Simulation and Optimization Production Planning:A Case Study[J].Research Memorandum,1988.

[7]G.V.Reklaitis,A.Ravindran,K.M.Ragsdell.Engineering Optimization:Methods and Applications[M].New York：John Wiley&Sons,1983.

[8]R.Fletcher.Practical Methods for Optimization(2ndEdition)[M].New York：John Wiley&Sons.1987.

[9]P.E.Gill,W.Murray,M.H.Wright,Practical Optimization[M].London,Academic Press,1981.

[10]A.M.Law,W.D.Kelton,Simulation Modeling and Analysis[M].New York:McGraw-Hill,2000.