面板數據聚類分析的投影尋蹤模型

徐華鋒 ，方志耕

（1．南京航空航天大學 經濟與管理學院,南京 210016;2.河南城建學院,河南 平頂山 467001）

0 引言

面板數據同時包含截面數據和時間序列,既具有空間維度特征又具有時間維度特征,近幾年在理論研究和應用研究上都得到了廣泛而深入的發展[1]。相關研究也表明利用面板數據建模取得了良好的效果,然而現有的理論和應用主要是從計量建模的角度研究,很少學者考慮面板數據在多元統計中的分析。國內學者朱建平曾對單指標面板數據的聚類分析進行了一定的研究,介紹了面板數據的統計描述方法,構造了面板數據之間相似性的統計指標,并在此基礎上提出了面板數據聚類分析的有效方法,為面板數據的多元統計分析開創了新的局面[2]。鄭兵云對多指標面板數據的聚類分析進行了研究[3],分析了面板數據的數據格式和數字特征,根據聚類分析原理,重新構造了多指標面板數據的距離函數和離差平方和函數,在此基礎上,說明了多指標面板數據的聚類分析過程并且進行了聚類實證分析,進一步推動了面板數據的多元統計分析。

投影尋蹤是一種新興的統計方法,是現代統計、應用數學與計算機技術的交叉學科，屬于前沿領域。投影尋蹤的基本思想是利用計算機技術，把多維數據通過某種組合，投影到低維子空間上，并通過極小化某個投影指標，尋找出能反映原多維數據結構或特征的投影，在低維空間上對數據結構進行分析，以達到研究和分析多維數據的目的。近年來,國內很多學者致力于該領域的研究工作，并將投影尋蹤方法有效地運用到聚類分析和評價當中，并對不同領域的實際問題進行了實證分析[4-11]，取得了一定的成效。但是以往的投影尋蹤聚類模型僅局限于研究截面數據，本文嘗試對面板數據運用投影尋蹤方法進行聚類分析，取得了良好的效果。

1 面板數據的數據格式和數字特征

多指標面板數據的結構要復雜一些,不同于單指標的數據可以由一個簡單的二維表來表示,嚴格上應該用三維表來表示,在平面上我們可以將其轉換為一個二級二維表的形式,如表1,研究總體共有N個,每個樣品的特征用p個指標（X1…X2…X3）表示,時間長度為 T, 則 Xij(t)表示第 i個樣品第j個指標在時間t的數值。

為了下邊討論的方便，這里給出多指標面板數據的幾個統計量。

(1)第j個指標在時間t的均值

表1 多指標面板數據

對多指標面板數據的聚類分析之所以比較困難,其中一個很大的原因在于其數據特點是三維空間上的,而投影尋蹤方法則有效地把高維數據投影到低維空間,故本文考慮把投影尋蹤的動態聚類模型運用到面板數據的聚類分析。

2 投影尋蹤動態聚類模型

PP的基本思路是,把高維數據通過某種組合投影到低維子空間上。對于投影到的構形,采用投影指標函數(即目標函數)來衡量投影暴露某種結構的可能性大小,尋找出使投影指標函數達到最優 (即能反映高維數據結構或特征)的投影值,然后根據該投影值來分析高維數據的結構特征。

用PP探索多維數據的結構或特征時一般采用迭代模式。首先根據經驗或猜想給定一個初始模型,其次把數據投影到低維空間上,找出數據與現有模型相差最大的投影,這表明在這個投影中含有現有模型中沒有反映的結構,然后把上述投影中所包含的結構并在現有模型上,得到改進了的新模型,再從這個新模型出發,重復以上步驟,直到數據與模型在任何投影空間都沒有明顯的差別為止。

用 xij(t),i=1,2,…，n;j=1,2,…，p;t=1,2,…，T 表示在時刻 t第i個樣本第j個指標,投影尋蹤動態聚類模型的建立步驟如下：

步驟1:數據標準化處理

由于各指標xij(t)的量綱不盡相同或數值范圍相差較大,因此在建模之前對數據進行標準化處理,標準化公式較多,可選擇采用,這里采用如下公式:

步驟2:線性投影

把高維的數據信息通過投影的方法轉化到低維空間,不但形象直觀,而且便于運用常規的方法進行分析處理。所謂投影實質上就是從不同的角度去觀察數據,尋找能夠最大程度地反映數據特征和最能充分挖掘數據信息的最佳觀察角度即最優投影方向。這里選用線性投影,即將高維數據投影到一維線性空間進行研究,實際上就是把矩陣族 (xij(t))n×p轉換(投影)成 n維壓縮向量族(zi(t))n×p

設 a={a1,a2,…，ap}為單位投影方向向量,則 xij(t)，i=1,2,…，t=1,2,…T的投影特征向量為

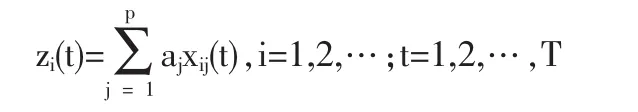
Ω={zi|zi=(zi(1),zi(2),…，zi(T))T,i=1,2,…，n}為投影特征向量集合。

步驟3: 構造投影指標函數

這是投影尋蹤動態聚類模型建立的關鍵,是高維數據向低維空間投影所遵循的規則,是尋找最優投影方向的依據,因此,只有構造合理的投影指標才能獲得科學的分類結果。下面依據動態聚類思想來構造投影指標。

首先依據實際情況或要求,采用動態聚類法將投影向量聚為k類,實現步驟如下：

(4）重復以上過程，得分類結果序列 V1=(Θ0，Θ1，Θ2…，Θl……)，

其次，構造投影指標函數。

類內樣本的鄰近程度用類內聚集度dd(a)表示為dd(a)=

其中dh(a)=(zi,zj)為類內聚積度,dd(a)越小,類內樣本的聚積程度越高。

因為不同的投影方向反映了數據的不同結構特征、不同綜合方式和不同數據挖掘途徑。在綜合過程中要求z(i)的分布特征應為:局部投影點盡可能密集,最好凝聚成若干個點團;而在整體上投影點團之間盡可能散開。基于此,投影指標函數可構造為

QQ(a)=ss(a)-dd(a)

顯然,ss(a)越大表示樣本間的距離越遠,即類間樣本分散越開;相反,dd(a)越小表示類內樣本之間的距離越近,即表示類內樣本越集中。因此,當QQ(a)取得最大值時,就實現了類間樣本盡量散開、類內樣本盡量集中的聚類目標。

步驟4：優化投影指標函數

根據上述分析,投影尋蹤動態聚類模型可以描述為如下的非線性優化問題。

此模型可以用加速遺傳算法求解,具體過程可見[11]。

3 實證分析

中國是世界第二大能源消費國。在不斷推進的工業化和城市化進程中，能源問題愈來愈成為中國經濟發展和社會進步的“瓶頸”，因此，正確認識中國能源消費結構狀況，實現能源、經濟和社會之間的協調發展，是開放的中國所面對和必須解決的重要課題。我國區域間的稟賦差異巨大,因此從區域角度出發,對不同地區的能源消費結構進行比較研究是很有意義的，以往的文獻在進行分析時往往采用時間序列分析或者截面數據分析，面板模型的采用可以綜合考慮地域差別和時間趨勢的影響,有助于克服單獨使用時間序列分析和截面分析方法的不足。本文以我國29個省區為研究對象，選取煤炭、原油、天然氣、電力各占能源消耗總量的比重四個指標，對1998-2007年間的數據運用面板數據聚類分析的投影尋蹤模型進行聚類分析。

首先,確定樣本分類數。這里將樣本分類為五類,即k=5。

其次,依據樣本指標值建立能源消費結構聚類模型,其中n=29,p=4,通過優化運算得最優投影方向向量為：

a=(0.22,0.20,0.34,0.24)

最后,模型輸出投影特征向量以及聚類結果。聚類分析結果顯示29個省區分類如下：

第一類，包括河北、山西、內蒙古、安徽和貴州。這些省份都位于中西部,有的是產煤大省,有的靠近產煤大省,而且之間的交通運輸非常方便。它們在生產和生活中的主要能源為煤炭。但這幾個省份的人均產值都比較低。

第二類，包括河南、湖北、湖南、云南、寧夏。是典型的中西部地區。這些省份的人均收入低,因而傾向于使用價格相對便宜的煤炭。而河南也是產煤省份,有許多重要的煤礦。

第三類，包括遼寧、吉林、山東、廣西、四川、重慶、甘肅,是我國典型的工業基地。

第四類，包括北京、天津、江蘇、浙江、福建、青海、新疆。這類省市的石油用量比重和煤炭用量比重都居中間位置。第四類的省份大致上可以分為兩種,一種是經濟發達地區,另一種是能源產地地區。經濟發達地區包括北京、天津、江蘇、浙江、福建。能源產地地區包括青海、新疆。

第五類，包括黑龍江、海南、上海和廣東。這些省市的能源結構以石油和煤炭為主,石油比重略大。其中,黑龍江和海南屬于能源大省,蘊藏著豐富的油氣資源，而上海和廣東卻屬于經濟發達、能源消耗大的省市。

4 結束語

面板數據的投影尋蹤動態聚類模型是基于面板數據的投影尋蹤和動態聚類的有機結合,充分發揮了投影尋蹤處理高維數據的突出優勢,融入了動態聚類的思想,同時又避免了投影尋蹤聚類模型的不足。實證分析表明面板數據的投影尋蹤動態聚類模型具有客觀性強及分類結果明確等優點,為多因素面板數據聚類分析問題的解決提供了一種新方法,也為投影尋蹤理論的推廣應用提出了一條新思路。

[1]Bonzo D.C.，Hermosilla A.Y.Clustering Panel Data via Perturbed Adaptive Simulated Annealing and Genetic Algorithms[J].Advances in Complex Systems,2002，(4).

[2]朱建平,陳民肯.面板數據的聚類分析及其應用[J].統計研究,2007，(4).

[3]鄭兵云.多指標面板數據的聚類分析及其應用[J].數理統計與管理,2008,27(2).

[4]金菊良,張欣莉,丁晶.評估洪水災情等級的投影尋蹤模型[J].系統工程理論與實踐,2002，22（2）.

[5]金菊良,汪淑娟,魏一鳴.動態多指標決策問題的投影尋蹤模型[J].中國管理科學,2004,(01).

[6]李世玲.基于投影尋蹤和遺傳算法的一種非線性系統建模方法[J].系統工程理論與實踐,2005,(04).

[7]金菊良,丁晶,魏一鳴,付強.解不確定型決策問題的投影尋蹤方法[J].系統工程理論與實踐,2003,(04)

[8]劉大秀，鄭祖國，葛毅雄.投影尋蹤回歸在試驗設計分析中的應用研究[J].數理統計與管理,1995,(01).

[9]張欣莉,王順久,丁晶.投影尋蹤方法在工程環境影響評價中的應用[J].系統工程理論與實踐,2002,(6)

[10]滕玉華,陳小霞.開放條件下中國工業能源強度的影響因素分析——基于31個行業面板數據的實證分析[J].新疆財經大學學報,2009,(01)

[11]金菊良,楊曉華,丁晶.基于實數編碼的加速遺傳算法[J].四川大學學報(工程科學版),2000,(4).