新混沌系統的自適應控制與噪聲中的同步研究

葉 慧,章亭芳

(江蘇科技大學 數理學院，江蘇 鎮江212003)

0 引言

由于混沌系統對初值的敏感性和長時間的不可預測性，控制混沌和混沌同步就成了混沌應用的關鍵環節，文獻[1]基于Lyapunov穩定性理論實現了連續混沌的自適應控制，文獻，文獻〔2-5〕采用了不同的方法實現混沌同步問題，但對于在噪聲作用下的異結構同步研究較少。 筆者在文獻[6]的基礎上接著對新混沌系統進行研究。首先分析它的動力學行為，在參數未知時設計一連續的自適應控制器，通過調整控制增益提高控制速度,并證明所給控制器能使受控混沌系統全局漸近穩定。接著研究在有界噪聲作用下文獻[6]中的兩個新混沌系統的異同步控制器的控制效果，用Matlab軟件進行數值仿真，檢驗了該控制器具的魯棒性和抗干擾能力。

1 新混沌系統的描述

1944年Nadolschi在研究剛運動時引入了一個新的系統,其特點是它的右端還有三個非線性項，在不同參數下可產生多個不同的吸引子。此新的混沌系統的數學模型為：

其中X=(x,y,z)T∈R3為系統的狀態變量，其中a,b,c為系統參數。

2 系統的穩定性分析

（1）對稱性和不變性。首先，注意到系統(1)在變換S：(X，Y，Z) →(-X，-Y，Z);S：(X，Y，Z)→(X，-Y，-Z);S：(X，Y，Z)→(-X，Y，-Z);下對于所有的參數 a，b，c 具有不變性，則這些變換表明系統關于x，y，z軸都是對稱的，即此系統關于原點對稱。顯然，坐標軸本身也是系統的解軌線，即，若t=0時有X=0，Y=0，Z=0，則對于所有的 t＞0，仍然有 X=0，Y=0，Z=0.更進一步說，對于t趨于0，坐標軸上所有的解軌線都趨向于原點。

（2）耗散性。當參數 a+b+c＜0 時，系統是耗散的。Δv==a+b+c它是收斂到一個零測度集=ea+b+c，即v(t)=v0e(a+b+c)t，其中v0是系統體積的初始值。

（3）與其他系統不同的是，令方程右端為零，我們得 該系統存在五個平衡點：］

由系統的Jacobi矩陣 可以求得系統的特征方程為：λ3-(a+b+c)λ2+(ab+ac+bc-mx2+z2+my2)λ+(mx2a-z2c+2mxyzmy2b-abc)=0上式中λ為待定的特征根將平衡點E0(0,0,0)代人 特 征 方 程 中 ， 有 ：λ3-(a+b+c)λ2+(ab+ac+bc)λ-abc=0，由Routh-Hurwitz判據，只要有 abc＞0,則 E0(0,0,0)是不穩定的。下面分析平衡點E1,E2,E3,E4的不穩定的參數條件，由系統(1)在變換S下及這些平衡點關于坐標軸的對稱性，所以只需要分析其中之一即可。如我們僅僅分析E1(的穩定性。將E1代入上述特征方程有λ3-(a+b+c)λ2+2abc+2m=0可得平衡點E1)不穩定的參數條件為：abc＞0， m＞0， a+b+c＜0

（4）根據上面的分析,根據Matlab軟件我們可畫出他的吸引子圖。見圖1。

當a=4.5,b=-12,c=-5,m=1/3時，系統是一個兩渦旋的混沌系統。當a=0.4.,b=-12,c=-5，m=1/3是一個四渦旋的混沌系統,且系統不存在Hopf分叉。

3 控制方法

下面考察將系統（1）全局漸近穩定到這五個平衡點E1,E2,E3,E4的控制問題。

黨的十八大報告高度評價：以毛澤東為核心的黨的第一代中央領導集體，在社會主義建設中取得的獨創性理論成果和巨大成就，為改革開放新的歷史時期開創中國特色社會主義道路“提供了寶貴經驗、理論準備、物質基礎”。這充分肯定了以毛澤東為核心的黨的第一代中央領導集體作為突破蘇聯模式、初步探索中國特色社會主義道路的奠基者的歷史性貢獻。

在控制律（2）中k用作自適應可調函數，β是自適應增益常數，β＞0改變β值可以適當改變自適應的速度。

定理1 通過自適應反饋控制器（2），受控閉環系統

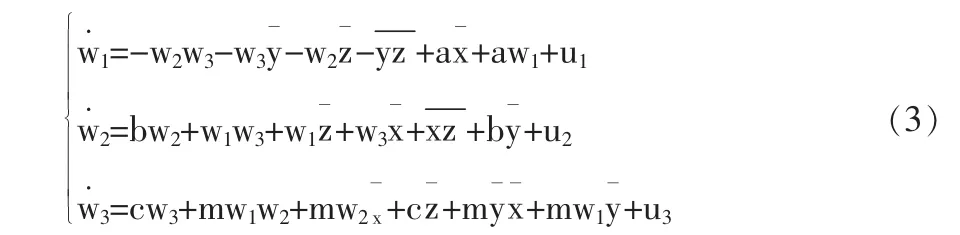
在零點全局漸近穩定，即原混沌系統（1）能被全局漸近穩定到它的五個不穩定的平衡點Ei。

證明:現構造如下的Lyapunov函數

即V˙負定.據 Lyapunov 穩定性定理，可知受控系統（3）的零解漸近穩定，亦即原系統（1）全局穩定于平衡點。

取 β=-5，采用（2）式控制律，以在平衡點 E0(0,0,0)為例，取初始值為（-1，-1，-1），作出受控閉環系統的三維相圖如圖2所示。

由圖2可知，在參數a未知的情況下（2）控制器，受控的閉環系統都是全局漸進穩定于平衡點E0(0,0,0)。

4 在噪聲下的兩類新混沌系統的異結構同步

在實際的物理環境中，噪聲是普遍存在的.實際的混沌系統是不可避免地受到噪聲的干擾.因此研究在外噪聲作用下同步方法[7]的魯棒性就極其重要.有界噪聲與理想的白噪聲相比，它是一個更切合實際的合理的噪聲模型.下面考慮外加有界噪聲對文獻[6]自適應同步方法的影響.

以新混沌系統（1）為例，注意觀察系統（1）可發現它還有三個非線性項，我們如果把它稍微變動就可發現它與最近陳關榮等最近研究Lorenz系統時，在Lorenz系統的第一個狀態變量上加上一個非線性項，從而得到的另外一個新的混沌系統

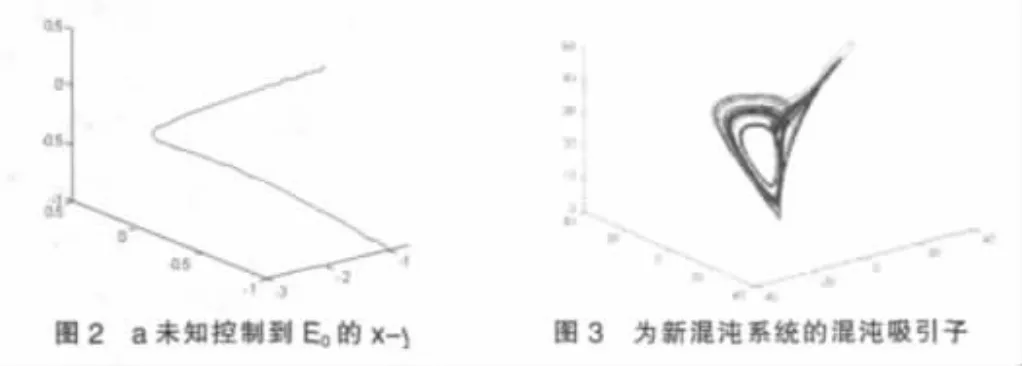
此系統與（1）系統有相同的結構特征，當a1,b1,c1的取值不同時它們有不同形式的混沌吸引子。在a1=40,b1=25,c1=-3時系統(4)的混沌吸引子圖3

文獻[6]給出了系統(1)和(4)在控制率為如下（5）時，這兩個新混沌系統的異結構同步。

其中β為大于0的數(β是自適應增益常數，改變它的值可以適當改變自適應的速度)。

現以將 Dξ(t)加到響應系統(4)式的右邊，ξ(t)=cos(Ωt+σB(t)+Γ)，其中 σ,Ω 為正的常數，B(t)是單位 Wiener過程，Γ 是[0,2π]之間均勻分布的隨機變量，D是噪聲強度。采用控制器(5),模擬數據仍用文獻[6]中的數據，選取有界噪聲ξ(t)中的參數Ω=1.0,σ=1.0,噪聲強度 D=0.5。 用 Matlab 仿真,畫出圖 4。

數值研究結果表明：在有界噪聲的作用下，自適應同步誤差在趨于零的過程中會出現一定的擾動，此時自適應同步誤差變得比較粗糙，但不影響最終的控制效果。

5 結論

對新混沌系統進行分析，得出其具有的五個平衡點都是不穩定的參數條件。接著運用反饋的控制方法，通過坐標變換，對混沌系統（1）進行了控制。在系統參數未知時，克服了一般的自適應控制中的控制律不連續這一缺點，設計一連續的自適應控制器使混沌系統漸近穩定。然后研究在有界噪聲作用下該系統的的異同步控制效果，表明了自適應控制器方法具有較強的魯棒性和抗干擾能力，數值仿真進一步說明這種方法是有效的。

[1]Loria,A，Panteley,Enijmeijer,H.Control of the Chaotic Doffing E-quation with Uncertainty in all Parameters[J].IEEE Transactions on Circuits and Systems I.1998,(45).

[2]Zhang Huaizhou,Qin Huashu.Adaptive Control of Chaotic Systems with Uncertainties[J].Int J.Bifurcation and Chaos,1998,8(10).

[3]蔡國梁,黃娟娟,超混沌Chen系統和超混沌Rossler系統的異結構同步,物理學報,2006.55(88).

[4]李爽,徐偉,李瑞紅等,異結構系統混沌同步的新方法，物理學報,2006.55(11).

[5]Julien Clinton Sprott Chaos and Time-Series Analysis[M].London：Oxford UniVersity Press,2003.

[6]葉慧，姚洪興，一類新混沌系統的控制與異結構同步及其在保密通信中的應用，江蘇科技大學學報，2007，(10).

[7]賈飛蕾，徐偉，一類參數不確定混沌系統的延遲同步[J].物理學報，2007,56（06）.