向 量 在 代 數 中 的 應 用

□陸金菊

( 山西省畜牧獸醫學校，山西 太原 030024)

我們知道向量是既有大小又有方向的量。它的廣泛應用滲透到各個領域。它是我們研究問題解決問題的有力工具。如：物理中存在大量的向量，位移、力、力矩、速度、加速度、電場強度等。至于向量在數學、計算機等自然科學中的應用就更廣泛，更有其用武之地。下面就向量在代數領域中的應用做一些探討。

一、運用向量知識證明某類等式

證明等式一般來說要進行繁雜的運算，如果等式具備向量在代數中的某些特征時，應用向量知識去證明，方法較為簡單。從而起到降低教學難度，提高學習能力的作用。

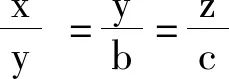
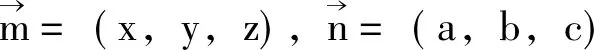
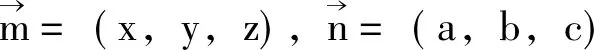
利用已知條件(x2+y2+z2)(a2+b2+c2)=(ax+by+cz)2可得 cos2θ= 1。

例2 用向量的數量積公式證明三角形的余弦定理如圖：已知：在△ABC中，a、b、c分別是三個內角∠A、∠B、∠C所對的邊。

求證： c2=a2+b2-2abcosC

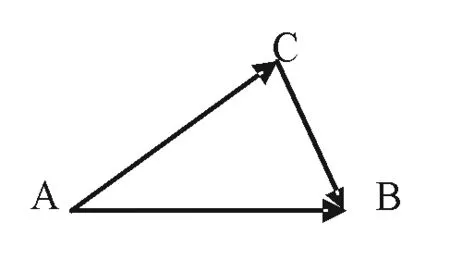
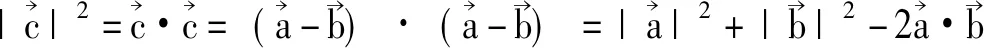
∴c2=a2+b2-2abcosC

二、運用向量知識證明某類不等式

證明不等式方法很多，但某些含有乘方之和或者乘積之和的不等式，運用向量的數量積公式證明會使證明過程更加直觀，更加簡捷。

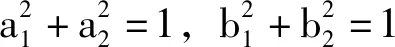
求證： -1≤a1b1+a2b2≤1

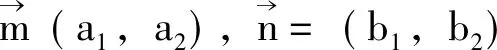
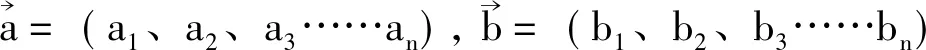
三、運用向量知識解決有關三角函數問題

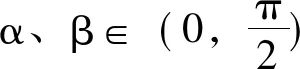
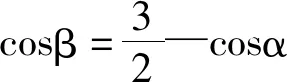
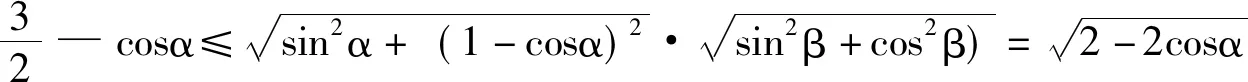
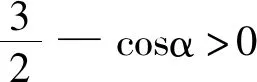
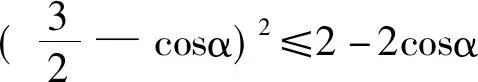
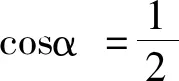
證明：設正n邊形A1A2A3…An-1An的邊A1A2與ox 軸的夾角為α，且設正n邊形的邊長為1。

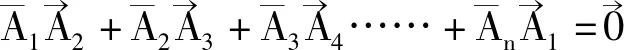
而 cos0=cos2)π

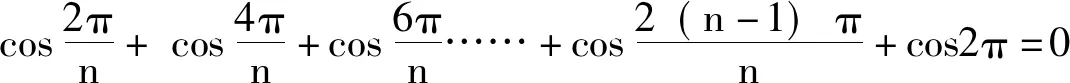
四、運用向量知識解決有關函數的最值問題

求函數的最值問題，有時候按照常規方法求解有一定的難度，當具備某些條件時，用向量知識解答，會使求解變得容易。

可見，用向量知識解決有關代數問題，主要用到向量的數量積公式。因此，關鍵是要善于觀察題目的結構特征，并由此巧妙地構造出向量的坐標，達到簡化問題、并迅速求解的目的。由此可見，向量的應用是數學教學中的難點與重點。要始終掌握向量基本定理公式，構造適當的向量，使向量運算順利進入計算與推理過程，從而解決面臨的問題。

參考文獻：

[1]鄧俊謙.應用數學基礎[M].上海：華東師范大學出版社,2000.

[2]李文林.中等職業教育國家規劃教材[M].北京：人民教育出版社,2005.

[3]嚴國良.善用向量工具，提高解題能力[J].數學教學，2003，(3).