基于ART神經網絡的FCM聚類多目標跟蹤方法

李 樂,嵇成新,王春雨

(海軍大連艦艇學院,大連 116018)

1 問題的提出

當雷達跟蹤空間目標時,往往接收到熱噪聲、虛警、背景雜波以及其他目標引起的回波,這些非目標回波使估計器進行錯誤的更新,估計器性能由此大大下降,有時甚至發生目標丟失現象。同時,多部雷達同時監視某一空域,在空域出現多批目標時,由于通信延遲、雷達天線掃描周期不同等原因,在某一時刻,融合中心接收到多部雷達的測量數據構成的空中態勢呈現出團狀,源于同一目標的測量不可能重合等特點,因此出現了各種數據關聯技術。隨著模糊理論處理技術和神經網絡技術研究的不斷深入,將模糊技術與神經網絡技術進行有機結合,應該說可以同時發揮以下優勢:模糊理論的邏輯推理能力,容易進行高階的信息處理優勢,神經網絡技術學習和自動模式識別,并且彌補各自的不足,這是對兩者結合的目標跟蹤算法進行深入研究的一種必然趨勢。

近年來,人們將應用模式識別理論中模糊和聚類理論運用于數據關聯的研究,其中基于模糊均值聚類的模糊C均值(FCM)算法研究比較廣泛。FCM算法是利用模糊均值聚類的原理,計算量測與航跡之間的隸屬陣,根據最大隸屬度確定量測與航跡的關聯關系。FCM算法的性能強烈地依賴類中心的初始化,但其初始類中心又是隨機選取的。如果能選擇與實際類中心近似的初始類中心,將減少算法的迭代次數,縮減聚類時間,并很快收斂于實際的類中心。

2 FCM算法

在眾多的模糊聚類算法中,應用最廣泛且較成功的是1974年由Dunn提出并由Bezdek加以推廣的FCM算法。FCM算法是把n個數據Xi(i=1,2,…,n)分成c個模糊簇,并求得每個簇的類中心,使目標函數達到最小。同時,FCM算法通過優化模糊目標函數得到每個樣本點相對類中心的隸屬度,自動對數據樣本進行分類,從而決定樣本點的分類。FCM算法的目標函數為:

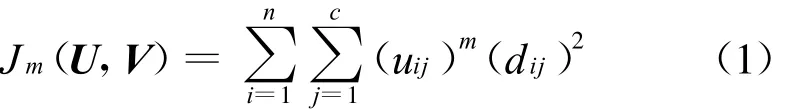
為使Jm最小,類中心和隸屬度更新如下:

當dij=0時,則 uij=1,uik=0,k≠j,i=1,2,…,n。

但其有一些自身的缺點:

(1)聚類的類數不能自動確定,使用時必須確定聚類的有效性準則;

(2)類中心的位置和特性不一定事先知道,必須由隨機初始化產生;

(3)對大數據集進行聚類時,運算開銷太大;

(4)在很多情況下,算法對噪音數據比較敏感。

3 ART神經網絡

3.1 ART神經網絡理論

神經網絡理論中的自適應諧振理論(ART)是由美國Boston大學的A.Grossberg和A.Carpentet提出的。ART是一種無教師、矢量聚類、競爭學習算法。它成功地解決了學習中的穩定性(固定某一分類集)與可塑性(調整網絡固有參數的學習狀態)之間的矛盾。

3.2 ART神經網絡學習方法

傳統ART神經網絡算法的學習方法詳見參考文獻[6]。

由于在實際情況中,各傳感器性能不盡相同以及外部條件等因素的影響,不一定會有多少個傳感器就反饋回多少個目標參數,由此造成空間向量分布不均勻的特點。初始設置的警戒參數在聚類過程中往往會存在主觀性和全局性等缺陷,使得分類效果不均,降低跟蹤精度,故對警戒參數調整規則如下:

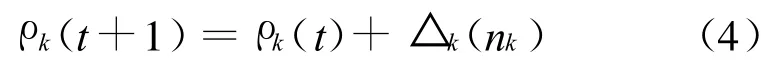
修正量△k(nk)使新的警戒參數和原始警戒參數與空間向量的密度成同向關系。當類別內包含較密集的輸入向量時差值較大,形成的新警戒參數值較大,在新一次聚類循環中此類將被細分為較多的子類別;而當類別內輸入向量較稀疏時差值較小,形成的新警戒參數值較小,在新一次聚類循環中此類別會被劃分為較少的幾個子類別。

4 多目標數據關聯

M個傳感器(局部節點)跟蹤T個目標的動力學方程為:

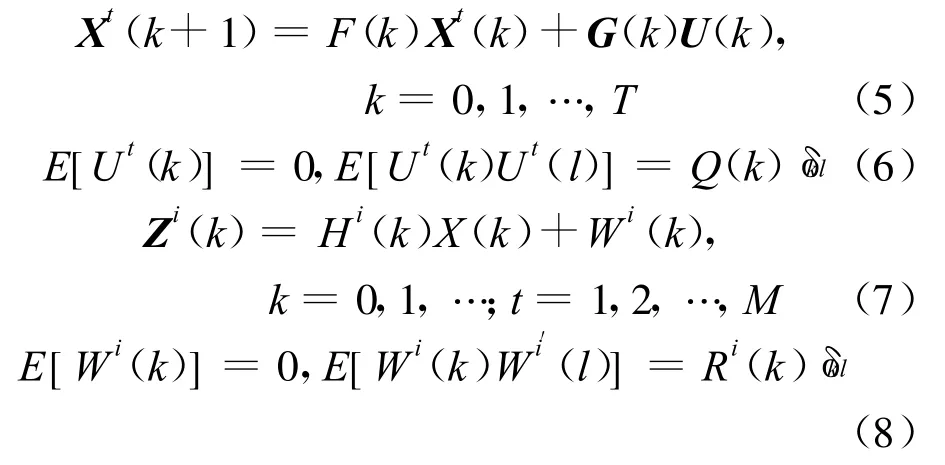
式中:X(k)為k時刻狀態向量;過程噪聲U(k)和測量噪聲Wi(k)均為高斯過程,協方差分別為Q(k)、R(k);Zi(k)為第i個傳感器在k時刻的測量矢量。

4.1 數據關聯過程

設有N個傳感器對M個目標進行跟蹤,在雜波環境下,每個傳感器得到的量測數據可能來自目標也可能來自雜波,這時就需要用數據關聯將傳感器的量測區分開來。把目標數作為聚類個數c,傳感器得到的觀測數據作為樣本點,目標狀態預測值作為類的中心,設傳感器融合系統系統已形成航跡,且各傳感器的量測數據在時間上同步,在空間上已轉換為同一坐標系,則數據關聯的具體步驟如下:

(1)由k時刻目標t的狀態融合估計,在Kalman狀態估計濾波后到k+1時刻各個目標的狀態預測 xj′(k+1/k)、新息vjt(k+1)及信息協方差陣Sjt(k+1)。目標狀態預測即為k+1時刻傳感器融合系統得到的量測分類中心作為ART神經網絡“粗聚類”的初始聚類中心。

(2)根據ART神經網絡學習方法對輸入數據Xi(i=1,2,…,n)按照以Kalman狀態估計濾波得到的初始聚類中心進行“粗聚類”。對于匹配度較差的量測點,很明顯是雜波,因此利用ART神經網絡先行排除。網絡收斂后,根據輸出節點的響應,完成樣本數據集的聚類。

(3)輸出聚類數目C和聚類中心Z={Z1,Z2,…,ZC}。

(4)進行模糊C均值聚類,計算各測量點對聚類中心的隸屬度矩陣U。對加權指數m的取值,文獻[3]根據聚類有效性問題結果,采用取值范圍1.5≤m＜2.5,選擇加權指數m=2。這是一個最簡潔的取值,較具有代表性。

由于任一目標只能有一個觀測量來自同一個傳感器,因此把多傳感器觀測數據聚類轉化為多個單傳感器聚類,把源于同一個傳感器的觀測量按最大隸屬度來分配給各個目標,這樣有效降低了聚類的復雜度,避免了錯誤關聯的概率,更符合實際。

因此本文基于ART神經網絡的FCM聚類算法大致可分為2個階段:第1階段,由ART神經網絡進行初聚類——“粗聚類”,在排除顯著的雜波干擾前提下得出聚類數目和各類中心點;第2階段,將第一階段的聚類輸出結果作為FCM聚類的初始輸入,進行迭代比較,直至收斂并輸出聚類信息。

4.2 數據融合與跟蹤濾波

4.2.1 傳感器觀測數據融合

由于每個傳感器測量誤差不盡相同,故σw2(i)可能兩兩不等,其中i=1,2,…,N。對經過數據關聯的某N個量測組成的一類C={Zi(tc)│i=1,2,…,N}作線性組合。

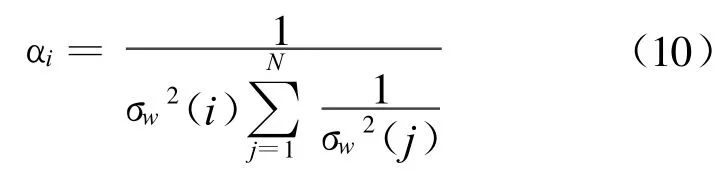
4.2.2 跟蹤濾波

完成量測與目標的互聯后,下一步便是更新目標的狀態,預測目標的新狀態了。對于新目標,則是產生目標的軌跡,同時預測其下一時刻的狀態。對于已測得的軌跡,利用Kalman濾波器得出當前時刻的狀態及下一時刻的估計狀態,計算步驟如下:

(1)驗前狀態估計(預測)方程:

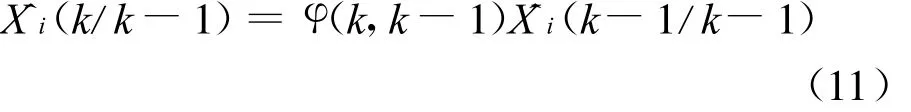
(2)驗后狀態估計(濾波)方程:

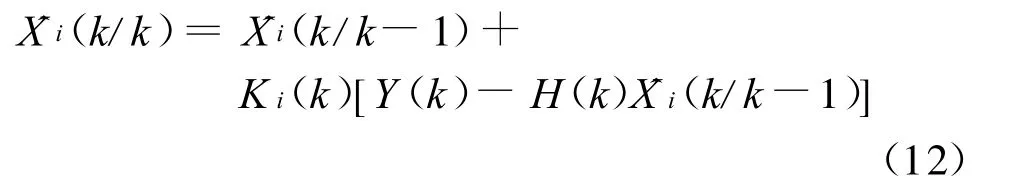
(3)卡爾曼濾波增益(最優增益)方程:

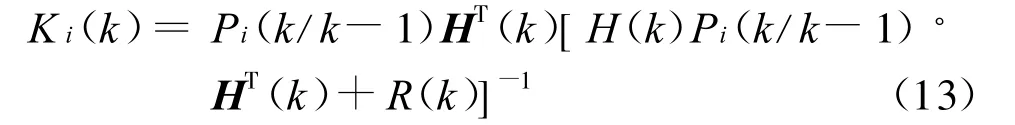
(4)驗前誤差協方差(預測)方程:

(5)驗后誤差協方差(濾波)方程:

5 仿真實驗

仿真戰場范圍是一個11 km×11 km的空間區域,仿真時間為40 s,其中雜波密度為1×10-5個/km3。假設只有位置測量可以利用,忽略目標在高度范圍內的變化。戰場中艦艇編隊共有2艘驅逐艦,采用大間距單縱隊防御隊形,每艘艦艇有兩部傳感器提供量測數據,融合中心設在第一艘艦艇上。仿真程序每隔1 s發送一批仿真數據,這些數據是傳感器在場景中采集到的信息,包括位置和速度,并進行100次Monte Carlo仿真實驗。

航路想定:本仿真采用4部傳感器實時提供的量測數據,傳感器的測量精度(均方誤差)為100 m,跟蹤2個做近似交叉機動的目標。

目標1:初始位置位于5000m,初始速度為200 m/s,初始加速度為-10 m/s2,目標以大約2°/s的角速度進行轉彎運動;

目標2:初始位置位于8 600 m,初始速度-200 m/s,初始加速度10 m/s,目標以大約2°/s的角速度進行轉彎運動;

其中,目標1與目標2在第10～25個采樣周期進行近似交叉機動,仿真及跟蹤軌跡如圖1(a)、(b)所示,。

圖1 跟蹤效果比較

由表1、2可明顯看出,在中等雜波條件下,初始機動跟蹤時,兩算法跟蹤精度及數據關聯正確率相差不大;但到兩目標進行交匯機動時(10～25 s左右),傳統算法跟蹤效能明顯不如改進后算法跟蹤效能,容易出現目標的合并或丟失,而錯誤估計甚至無法估計目標,增加了誤警概率,導致跟蹤精度明顯降低,見表1、2。從反應時間上,傳統算法為 4.5 s,本文提出的模型算法比其提高了近50%,為2.4 s,為武器系統的有效利用,提高編隊整體防御預警時間,提供了有力的基礎。

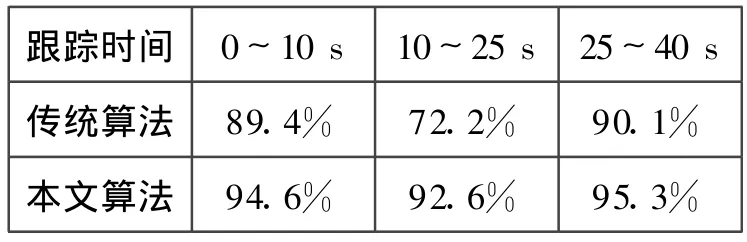
表1 兩種跟蹤算法平均關聯正確率對比

表2 兩種跟蹤算法跟蹤精度對比(x軸均方誤差平均值)

6 結論

本文利用ART算法自動聚類的優點對數據集先行“粗聚類”,克服了FCM算法的性能強烈依賴類中心的初始化,初始類中心又是隨機選取的不足。通過將改進的ART神經網絡與FCM算法的結合,達到了減少算法的迭代次數,縮減聚類時間,并很快收斂于實際的類中心的效果。仿真實驗表明,對觀測值進行ART-FCM聚類處理后的濾波跟蹤航跡精度較高,時間較短,對多目標跟蹤理論的實際應用有一定的理論參考價值。

[1]胡煒薇,李爭,蒲書紹,楊蘋元.雜波環境下雷達組網的多目標聚類融合跟蹤[J].哈爾濱工程大學學報,2006,27(4):584-587.

[2]Bezdek C James.Convergence theoryfor fuzzy cmeans:counter examples and repairs[J].IEEE Transaction on Systems,Man and Cybernetics,1987,17(6):889-914.

[3]陳松生.王蔚.改進的快速模糊C-均值聚類算法[J].計算機工程與應用,2007,43(10):167-169.

[4]由大德,程樹昌,嵇成新,等.火控理論基礎[M].大連:海軍大連艦艇學院,2005.

[5]錢曉東.基于改進ART2算法的數據聚類方法[J].計算機工程與設計,2007,28(11):2629-2632.

[6]王永驥.涂健.神經元網絡控制[M].北京:機械工業出版社,1999.

[7]徐毓,李鋒,金以慧.基于聚類融合的多目標跟蹤算法[J].傳感器技術,2002,21(7):31-34.