基于Simulink的無刷直流電機仿真模型新策略

陳晉瑋

(船舶重工集團公司 723所,揚州225001)

0 引 言

隨著電力電子、集成電路、電機控制理論和永磁材料的快速發展,永磁無刷直流電機廣泛應用于工業控制的各個領域。永磁無刷直流電機結構簡單、運行可靠、維護方便,具有良好的調速性能。為了便于理論分析和驗證各種控制算法和策略,正確建立直流無刷電機控制系統的模型就顯得非常重要。本文利用Matlab軟件下Simulink仿真工具箱對直流無刷電機控制系統進行詳細的建模與仿真,克服了用電力系統模塊庫分析不夠深入、仿真欠靈活等缺點。仿真結果表明該仿真模型與理論分析相吻合,驗證了仿真模型的正確性和有效性。

1 無刷直流電機的數學模型

無刷直流電機的運行特性涉及非線性理論及數值解法等諸多問題,在一般工程應用上通常均作如下假定:(1)各相繞組對稱,其對應的電路單元完全一致,相應的電氣時間常數忽略不計;(2)忽略齒槽、換相過程和電樞反應等的影響;(3)控制電路在開關狀態下工作,功率開關管為理想開關,功耗不計;(4)磁路不飽和,不計渦流和磁滯損耗。

由于直流無刷方波電動機的氣隙磁場、反電動勢以及電流是非正弦的,因此采用d-q變換已不是有效的分析方法,通常直接利用電動機本身的相變量來建立數學模型。

1.1 電壓方程

BLDCM三相定子電壓的平衡方程可以用以下的狀態方程表示:

式中:Rs為三相定子繞組的相電阻;Ia,Ib,Ic為三相定子相電流;Laa,Lab,Lac,Lba,Lbb,Lbc,Lc a,Lc b,Lcc為三相定子繞組之間的互感;Ea,Eb,Ec為三相定子的反電動勢;p為微分算子;Vn為三相定子繞組中點電壓:

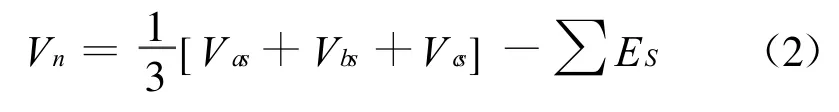
式中:∑ES為瞬時三相定子的反電動勢之和,反電勢為理想梯形波,幅值為:

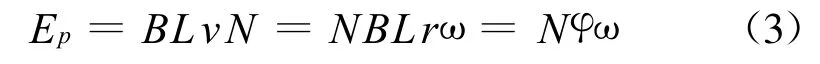
式中:B為磁場強度;L為電機長度;N為每相匝數;ω為電機轉動角速度。

這里假設電感不隨位置而改變,反電勢為理想梯形波。在360°電角度內,轉子的磁阻不隨轉子位置的變化而變化,并假定三相繞組對稱,則有Ia+Ib+Ic=0,并有:

式中:Ea,Ec,Ec為三相反電動勢信號。

1.2 轉矩方程和運動方程

轉矩方程為:

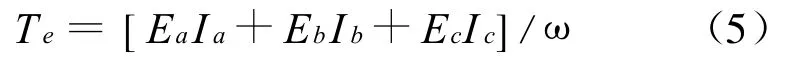
運動方程為:

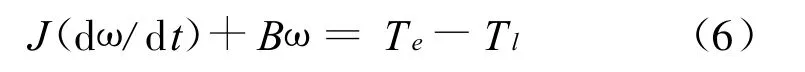
式中:T1為負載轉矩;J為轉動慣量;B為摩擦系數。

電機轉動角度函數為:dθ/dt=(P/2)×ω,P為電機極數。

2 基于Simulink的BLDCM 控制系統模型的建立

目前,Simulink仿真平臺由于操作簡便、模型庫豐富、仿真效率較高等優點,得到科技界廣泛認可。本文充分利用 Simulink現有資源,在分析BLDCM數學模型的基礎上,對永磁無刷直流電機建模原理和實現過程進行了詳細闡釋。其系統框圖如圖1所示。BLDCM控制系統仿真模型主要包括:BLDCM本體模塊、速度控制模塊、觸發邏輯控制驅動逆變模塊和轉矩計算模塊。通過這些功能模塊的有機整合,成功搭建出了BLDCM控制系統的仿真模型,并實現了閉環的控制算法。

圖1 BLDCM控制系統仿真模型

2.1 BLDCM本體模塊

BLDCM系統狀態方程為 X′=AX+Bu,由式(7)、(8)、(9)、(10)、(11)建立在整個控制系統的仿真模型中。BLDCM 仿真模型如圖2。

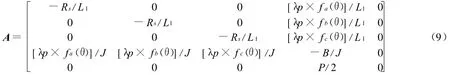
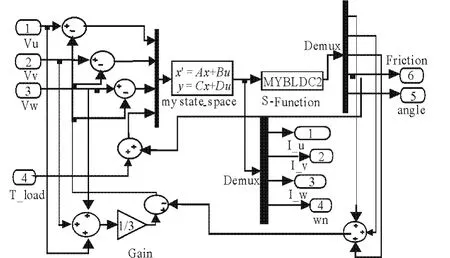
圖2 BLDCM仿真模型

BLDCM本體模塊是最重要的部分,該模塊根據BLDCM電壓方程式(4)求取BLDCM三相相電流,由式(4)可得,要獲得三相相電流信號 Ia、Ib、Ic,首先要求得三相反電動勢信號 Ea、Eb、Ec。在BLDCM建模過程中,梯形波反電動勢的求取方法一直是較難解決的問題,反電動勢波形不理想會造成轉矩脈動增大、相電流波形不理想等問題,嚴重時會導致換向失敗,電機失控。因此,獲得理想的反電動勢波形是BLDCM仿真建模的關鍵問題之一。

S函數模型提供了了解電機內部情況的手段,只要電機數學模型足夠精細,就能夠通過仿真觀察到電機內部的仿真結果,因此該模型在建模分析時具有較大的靈活性。本模塊S-function采用分段線性法建立梯形波反電動勢波形,將一個運行周期0～360°分為 6個階段 ,每 60°為一個換向階段,每一相的每一個運行階段都可用一段直線進行表示,根據某一時刻的轉子位置和轉速信號,確定該時刻各相所處的運行狀態,通過直線方程即可求得反電動勢波形。分段線性法簡單易行且精度較高,能夠較好地滿足建模仿真的設計要求。

2.2 速度和轉矩計算模塊

速度和轉矩計算模塊如圖3所示。該模塊采用了通用的PID調節器進行速度和電流的控制。根據速度給定信號、速度反饋信號,用編程S-function計算所需力矩和電機定子每相電流。

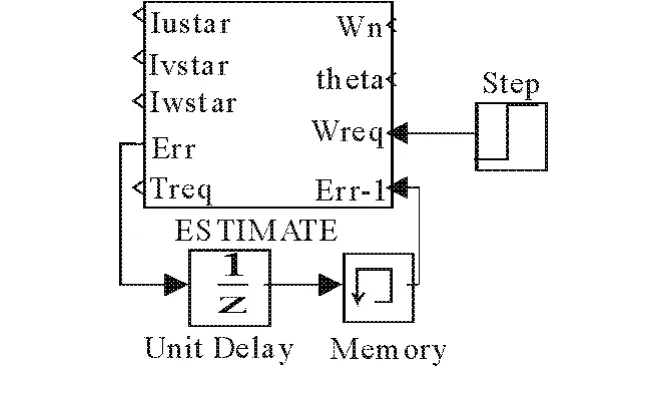
圖3 速度和轉矩計算模塊

力矩公式為:

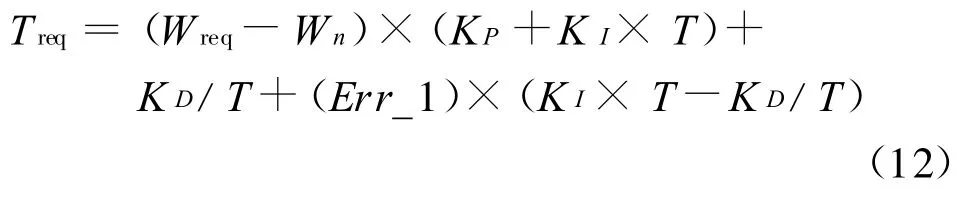
式中:Treq為給定速度所需力矩;Wn為反饋速度;Wreq為給定速度,KP、KI、KD分別為比例、積分和微分參數;Err_1為前一時刻的速度誤差。

電流公式為:

2.3 換相邏輯模塊

BLDCM控制系統中逆變器的可靠換相,是通過BLDCM內部的轉子位置信號進行控制的。IUSTAR_in,IVSTAR_in,IWSTAR_in和反電動勢波形相似,包含了轉子位置信息。該模塊包含三個子模塊(如圖4),均用Stateflow Charts圖形化建立兩相導通三相六狀態BLDCM換相邏輯。

3 仿真試驗及結果

根據上述所建立的BLDCM控制系統的仿真模型,進行了轉速調節的仿真試驗。仿真所用電機數據:定子繞組電阻Rs=0.702 9 Ω,相電感 L-M=4.238mH,轉動慣量J=2kgcm2,額定電流I=4.5 A,額定轉速n0=480 rpm,額定轉矩 T=6 Nm,極對數 P=2。仿真條件:采用多步解算器ode113算法,變步長。

圖4 換相邏輯仿真模型

從圖5可以看出,系統從零速啟動時,仿真模型S-function需要時間計算反電動勢來確定轉子位置,之后保持最大啟動轉矩,轉速響應有超調,系統在很短的時間內就進入了穩態。仿真結果顯示穩態運行時轉速無靜差,與理論情況相吻合。由仿真波形可以看出,在N=75 rpm的參考轉速下,系統響應快速且平穩,系統具有較好的靜、動態特性。仿真結果證明了本文所采用這種BLDCM仿真建模方法的有效性,同時也證實了反電動勢控制法的可行性。

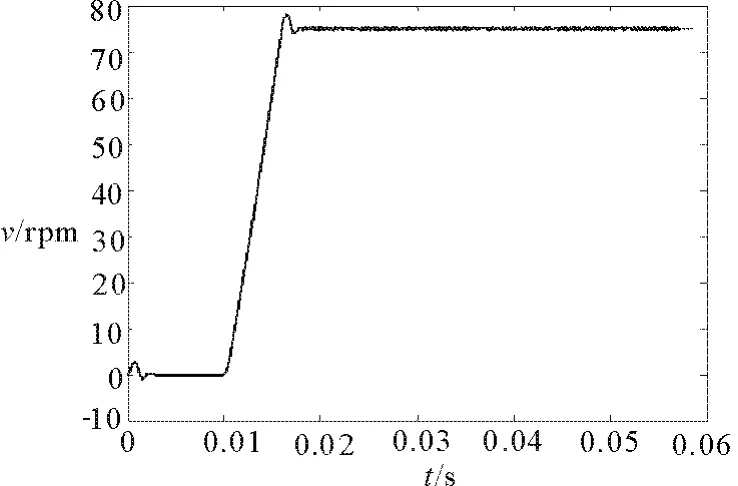
圖5 系統速度相應曲線

4 結論

本文在分析BLDCM數學模型的基礎上,先后對永磁無刷直流電機的電路模型和S函數模型的建模原理及實現方法進行了闡述,建立了BLDCM控制系統仿真模型。在上述仿真的基礎上,控制器可采用不同的控制算法,通過該仿真系統的響應來驗證和改進控制策略,它為分析和設計直流無刷電機控制系統提供了一個理想試驗平臺。

[1]Krishnan R.Electric motor drives-modeling,analysis and control[M].New Delhi:Prentice Hall of India Private Limited,2005.

[2]陶桂林,馬志云,周理兵,等.永磁無刷電機的建模與仿真分析[J].華中科技大學學報,2003,31(1):82-85.[3]吳影生,胡虔生.無刷直流電機系統仿真模型與改進[J].機械制造與自動化,2003(5):54-57.

[4]張琛.直流無刷電動機原理及應用[M].北京:機械工業出版社,1996.