幾種不同模型參數估計法的性能分析

聶建棟,衛紅凱,李 猛

(1.海軍駐武漢438廠軍事代表室,武漢430033;2.海軍工程大學,武漢 430033;3.海軍 704廠,青島 266109)

0 引 言

功率譜估計是利用給定的樣本估計隨機信號的功率譜密度,表征信號能量隨頻率的分布特性。最初的譜估計方法有周期圖法和自相關法,稱為經典功率譜估計法。周期圖法假設觀察數據區域外的數據為零,自相關法假設數據在延遲窗以外的自相關函數為零,2種方法均無法實現功率譜密度原始定義中的求均值和求極限的運算,使得其在功率譜估計中不僅方差性能較差,而且分辨率較低,難以與實際功率譜匹配。

為了克服這些缺點,Yule通過用線性回歸方程模擬時間序列,奠定了現代譜估計的基礎。隨后,國內外學者在此基礎上進行研究和改進,極大促進了現代譜估計法的發展。

參數模型法是現代譜估計的重要內容,它將信號看成是隨機輸入序列通過線性系統的輸出,由此建立模型來估計信號的功率譜。參數模型估計法主要有自回歸(AR)模型、移動平均(MA)模型和自回歸-移動平均(ARMA)模型。

AR模型是全極點模型,由線性方程組描述;MA模型是全零點模型,可用高階的AR模型來近似;ARMA模型是極點和零點共存的模型,由非線性方程描述。本文主要分析AR模型對不同參數的估計方法及ARMA模型的性能,并通過仿真實例研究了不同方法對模型參數估計精度的影響。

1 AR模型

對于AR模型,其數學表示式為:

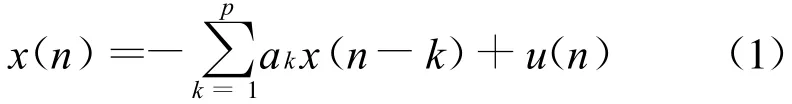
式中:u(n)、x(n)為實平穩的隨機信號,u(n)為白噪聲,方差為 σ2。

則其正則方程為:

式中:rx(m)為 x(n)的自相關函數;a1,…,ap,σ2為p階AR模型的待求參數。

若已知自相關函數rx(0),rx(1),…,rx(p),根據正則方程求出模型參數,并估計出信號x(n)的功率譜。當只約束前向預測誤差,即為直接法;當對前后向預測誤差均做約束時,即為Burg算法。

2 ARMA模型

ARMA模型是AR模型及MA模型的綜合。ARMA模型的求解步驟為:根據相關函數得到AR參數a(k),k=1,…,p,并據此用有限沖激響應(FIR)濾波器對輸入數據進行濾波,近似得到MA模型,求得MA參數b(k),k=1,…,q,從而得到ARMA模型的功率譜。根據AR模型及MA模型正則方程的推導,則可得 ARMA模型的正則方程為:

式中:h(k)為a(k)和b(k)的函數。

3 仿真實例

算例中,仿真信號x(n)為白噪聲通過三階FIR系統后輸出信號混疊3個不同頻率的實正弦信號。白噪聲的均值為零,方差為1。各正弦信號的歸一化頻率為 f1=0.18,f2=0.3,f3=0.31;幅度為A1=1.4,A2=52.6,A3=57.2。

3.1 AR模型自相關法估計信號功率譜

由于模型參數估計中,模型階數的選擇也會對模型參數的求解精度產生影響,因此,在仿真中也充分考慮了這一點,分析比較了不同階次對參數估計的影響。圖1為模型階數p=5,10,15,20時信號的頻譜估計圖。

圖1 自相關法不同階數下信號功率譜估計

由圖1可知,自相關法對小信噪比信號(f1=0.18)識別能力差,譜估計質量與模型階次的取值有直接關系,當模型階數較小時,無法分辨出相鄰頻率(f2=0.3,f3=0.31)的信號;隨著階次的增大,其對相鄰頻率的分辨力提高,能識別出相鄰頻率信號,但可能產生譜分裂現象(如p=25時,在0.18附近)。

3.2 AR模型Burg法估計信號功率譜

同樣在仿真中,也比較不同階次下對Burg法參數估計精度的影響,并將估計結果與自相關法的估計結果進行比較。圖2為模型階數為p=5,10,15,20時信號的頻譜估計圖。

圖2 Burg法不同階數下信號功率譜估計

由圖2可知,Burg法對功率譜的估計效果要好于自相關法,這是由于其對前后向預測誤差均有約束。因此,Burg法不僅能識別小信噪比信號(f1=0.18),而且可識別相鄰峰值的2個信號(f2=0.3,f3=0.31)。隨著模型階次的增加,信號的分辨率增大,但會產生虛假的峰值(如階數p=25時)。

3.3 ARMA模型估計信號功率譜

仿真條件同上,則不同階次下ARMA模型估計的功率譜如圖3所示。

圖3 ARMA模型不同階次下,不同時延對應的功率譜估計

由圖3可知:ARMA模型對功率譜的估計效果與模型階次及信號自相關函數最大延遲的選取有關。當模型階次選擇不恰當時(p=4,q=5),無法識別小信噪比信號。模型階次確定后,當最大延遲取值為40時,對小信噪比信號(f1=0.18)的識別不明顯,且由于MA部分的加入,使得波谷產生,模型對信號譜估計比較容易產生頻率漂移現象。

4 結束語

參數模型法在現代譜估計中具有重要作用,信號功率譜的估計精度不僅受不同參數估計方法的影響,也受模型階次的影響。當階次選擇過低時,譜的平滑度好,但分辨率差;當階次選擇過高時,容易產生虛假峰值。因此,階次的選擇需要根據實際問題,具體分析,通常是對結果做多次比較后,予以確定。

[1]Hayes M H.StatisticalDigitalSignal Processing and Modeling[M].New York:John Wiley&Sons,Inc.,1996.

[2]胡廣書.數字信號處理[M].北京:清華大學出版社,2003.

[3]徐立軍,張銳,楊紅兵.A RM A譜估計簡介及方法[J].重慶科技學院學報,2005(2):78-80.