干涉儀測向中相關處理算法的研究

王 磊,束 坤

(1.江蘇科技大學,鎮(zhèn)江212003;2.船舶重工集團公司723所,揚州 225001))

0 引 言

相位干涉儀測向體制具有測向精度高、算法簡單、實時性好等優(yōu)點。為了進一步提高測向精度和抗多徑能力,干涉儀測向設備一般要使用大于半波長的基線,此時測量的相位差會出現多值,即相位差模糊。雖然可以采用長短基線結合的方法解決相位差模糊問題,但這不僅使算法更加復雜,而且設備量將會隨測向精度的提高而大大增加。

相關處理算法應用于干涉儀測向體制后,使干涉儀測向體制不再受半波長的約束,提高了測向精度,解決了相位差模糊與提高測向精度之間的矛盾。

1 干涉儀測向體制的基本原理

干涉儀測向的實質就是通過測量空間來波信號在接收天線上形成的相位差后確定空間來波信號的到達角。以2個天線單元陣為例(見圖1),介紹干涉儀測向體制的基本原理。

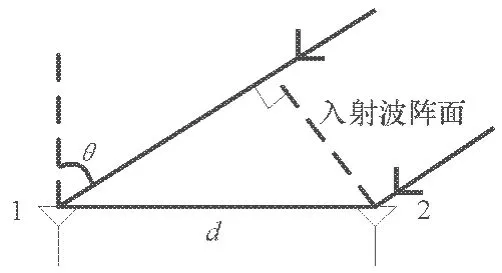
圖1 干涉儀測向原理圖

圖1中d為天線1與天線2之間的基線長,θ為入射波的到達角度,則相位差為:

式中:λ為入射波波長。

所以知道相位差后就可求出入射波到達角度:

在式(1)中,當d≥λ/2時 ,φ的取值會超出[-π,+π]的范圍。相位差 φ是由鑒相器測得的,而鑒相器的輸出范圍只能在[-π,+π]之內,是以2π為周期的,所以在d≥λ/2時相位差會出現相位差模糊,隨之帶來的就是更多的測向模糊。

針對上述情況,可以得到以下2種解決相位差模糊的方法:

(1)采用較小口徑的天線陣,d＜λ/2;

(2)采用長短基線相結合的測向體制。

下面分析干涉儀測向體制的測向誤差。對式(1)求全微分,可得:

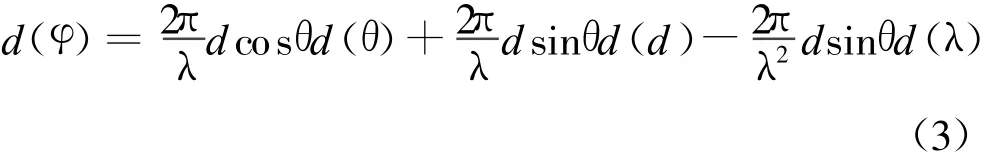
整理上式,用增量表示,可得:

忽略掉天線基線d變化造成的誤差,通常頻率變化誤差也可忽略,則測向誤差可表示成:

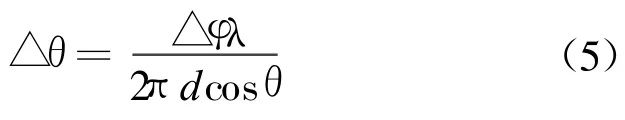
由上式可知:

(1)測向誤差主要是由測量的相位差誤差引起的;

(2)當 θ=0°時 ,測向誤差最小;當 θ=90°時,測向誤差最大,此時干涉儀已經失去了測向功能;

(3)基線長度d越長,測向誤差越小,測向精度越高。

綜上可知,在傳統(tǒng)的干涉儀測向中,d＜λ/2可消除相位差模糊,但測向精度很不理想,當增大基線長度d后,雖然可提高測向精度,但相位差模糊就無法消除了。這就是消除相位差模糊和提高測向精度之間的矛盾。

2 相關干涉儀

為了解決相位差模糊與測向精度之間的矛盾,可以在干涉儀測向中采用相關處理算法,即用相關干涉儀解決此矛盾。相關干涉儀測向技術是在干涉儀測向技術的基礎上發(fā)展而成的,它是通過比較獲取的入射波相位差與事先已存的各方位入射波相位差的相關性來得到入射波方向的。以多單元均勻圓陣為例,在多單元圓陣中,選取若干個天線對,對于一個確定入射角的入射信號,從這些天線對可以測得相應的相位差,這些相位差值由天線陣的結構決定。由已知的天線陣結構可以通過理論計算得出相位差值,也可以通過實際測量得出。在360°全方位上,每隔一固定的間隔選取一個方向ωi(i=1,2,…,n),每一個方向有若干個天線對的相位差值φj(j=1,2,…,m)相對應,m為選取的天線對數量。由這些天線對得到的相位差值稱為相關干涉儀測向體制的原始相位樣本。當一個實際的入射信號入射到天線陣上時,系統(tǒng)測量出一組相位差,然后將這一組值和系統(tǒng)原始相位樣本進行相關處理,可得出它們的相關系數,相關系數的最大值對應的角度就是入射信號的到達角度。

下面以五單元均勻圓陣為例來具體分析相關處理算法。五單元均勻圓陣如圖2所示。

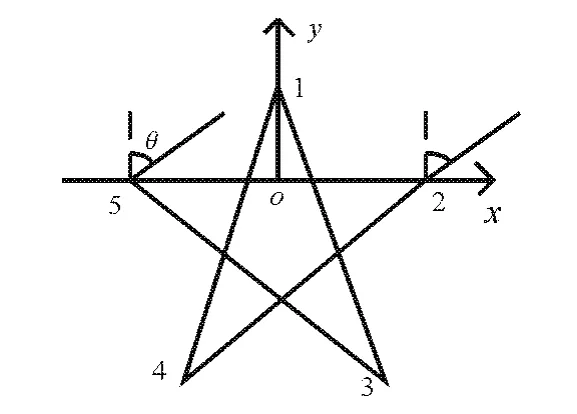
圖2 五單元均勻圓陣原理圖

5個天線的位置如圖所示,由5個天線形成的5條基線為基線1-3、基線2-4、基線3-5、基線4-1、基線5-2,長度均為d,建立如圖所示坐標,基線5-2與x軸重疊,y軸穿過天線1,基線5-2的法線平行與y軸,θ為入射波方向,λ為入射波波長,則基線5-2對應的相位差為:

以此類推可得其它4條基線對應的相位差為:

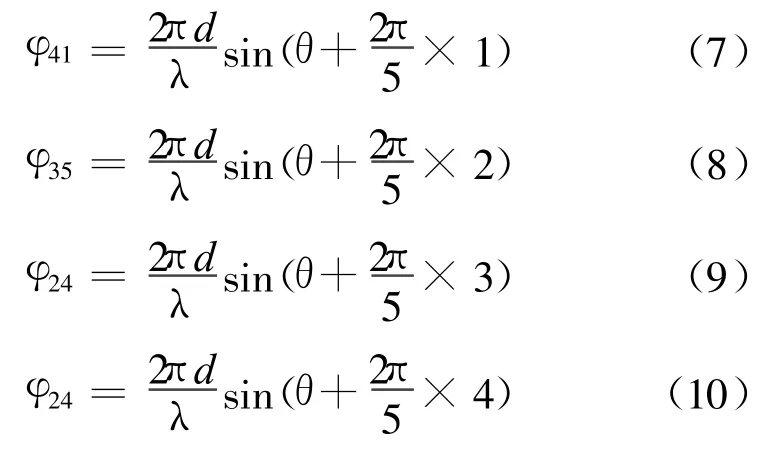
在360°的方向上以5°為間隔可取到73個方向ωi(i=1,2,…,73),方向 ωi對應的相位差為 φi=為第 i 個方向上基線5-2上的相位差),設實際入射信號方向為50°,則此方向上的相位差可求得為分別為實際來波方向上對應5條基線上的相位差,可得 Ψ和φi的相關系數為:

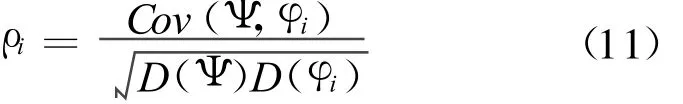
式中 :Cov(Ψ,φi)為 Ψ和φi的協(xié)方差 ;D(Ψ)和D(φi)分別為 Ψ和φi的方差,取基線長度與入射波波長之比為1/2,圖3為對此算法仿真的結果。

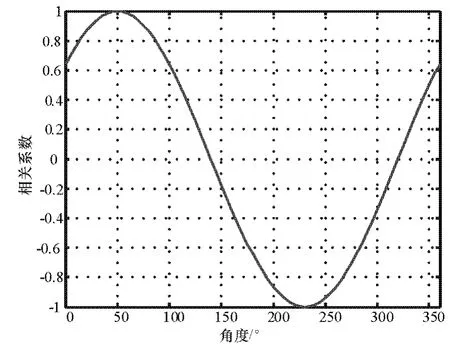
圖3 d/λ=1/2時的相關圖

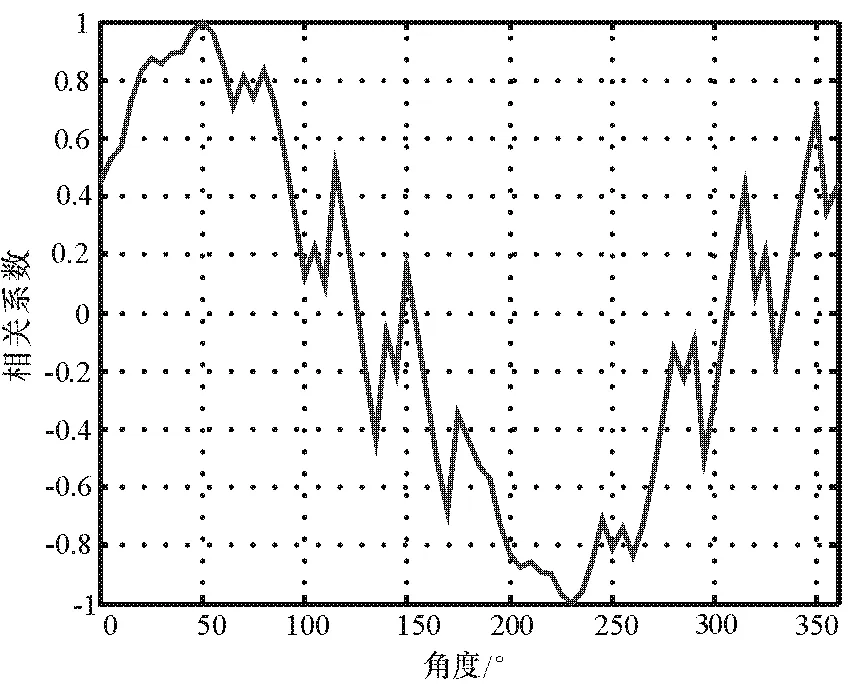
圖4 d/λ=3/2時的相關圖

由圖 3可知,在 50°處的相關系數為 1,即 50°方向有入射信號,但此圖中入射信號方向處過于平滑,測向精度不高。圖3在與50°方向相差約180°的230°方向上的相關系數為-1,這是因為50°方向上的相位差與此方向上的原始相位樣本大小相等,方向相反,形成了負相關。由上面分析可知,增大基線長度可提高測向精度,如圖4所示,在50°方向上有比較尖銳的峰,測向精度被提高。

3 其它兩種處理算法的研究

下面介紹的兩種算法的仿真結果都是在上一節(jié)給出的五單元均勻圓陣下實現的。

第一種處理算法是基于最小二乘估計的,它不是求實際入射信號的相位差與原始相位差的相關系數,而是通過求對應基線上實際入射信號的相位差與原始相位差的誤差平方和最小值來確定入射信號方向的,代價函數如下式:

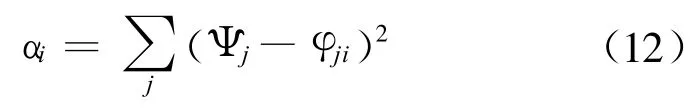
式中:j=1,2,…,5;i=1,2,…,73;Ψj為實際入射信號第j個基線上的相位差;φji為第j個基線在第i個方向上的原始相位差。

使αi最小的即為實際入射信號的到達角度。

由圖5和圖6可知,最小值在 50°處,所以入射信號角度為50°,且增大天線口徑后,圖6中50°處圖形較尖銳,由此可知此處理算法在基線長大于半波長時測向精度得到了提高且無測向模糊。

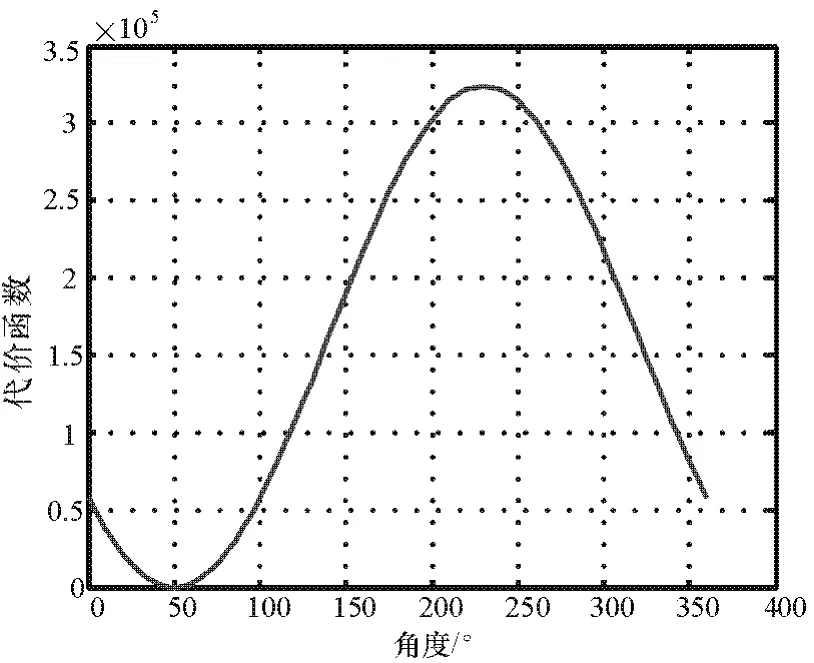
圖5 d/λ=1/2時的相關圖

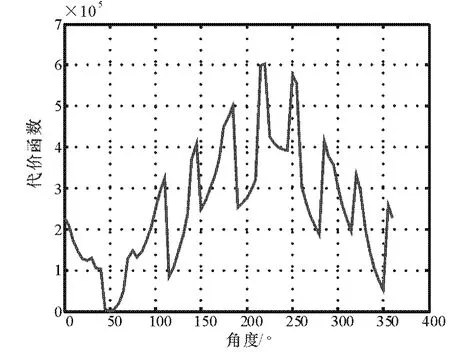
圖6 d/λ=3/2時的相關圖

第二種處理算法可以避免鑒相時的三角運算,把代價函數的運算從復數域簡化到實數域,減小了運算量,把原始相位的余弦 cosφji和正弦 sinφji與實際測得入射信號的余弦cosΨj和正弦sinΨj作相關運算后再把相關運算得到的值作歸一化處理,如下:

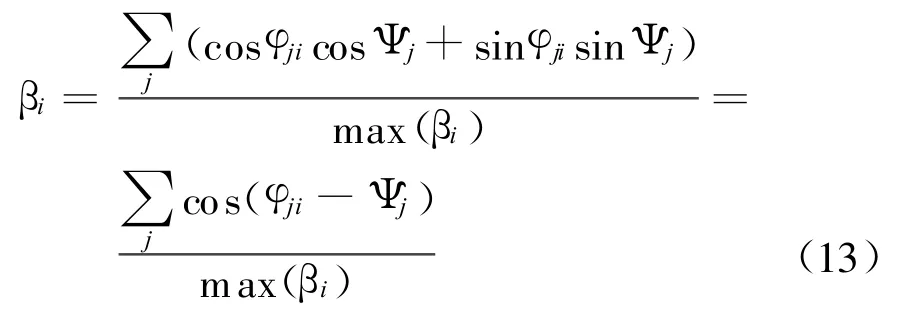
式中:max(βi)為 βi的最大值 。

仿真結果如圖7～8所示。

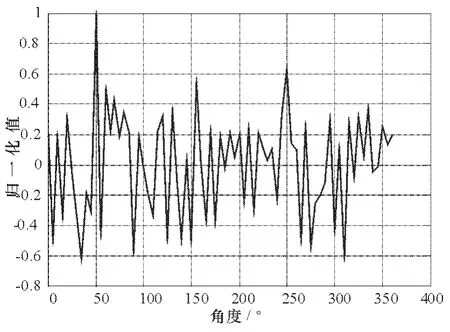
圖7 d/λ=1/2時的相關圖

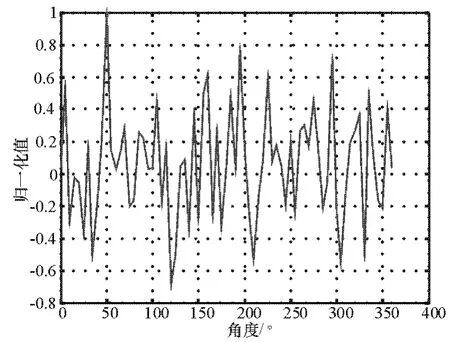
圖8 d/λ=3/2時的相關圖

由圖7可知,當d/λ=1/2時此處理方法的精度已明顯好于前面提到的處理算法,從圖8可以知道,當增大天線口徑后,相比較于圖7,測向精度卻沒有明顯變化,但其本身精度已經明顯高于前面算法的精度了。

4 結論

相關處理算法是相關干涉儀設計中重要的一項,它能夠在保證不出現相位差模糊的情況下使用大口徑天線來提高測向精度與抗干擾能力,對入射波的波前失真也有一定的抑制作用。現代的數字信號處理技術可以使相關處理算法更加易于實現,只需存儲采集到的原始相位樣本后,把實際的入射波相位差與已經存儲的原始相位樣本進行相關匹配處理即可。當原始相位差樣本通過實際測量得出時,那么原始相位差樣本就包含了系統(tǒng)的固有偏差、設備制造誤差和入射信號的所有相位信息,所以設備本身能夠達到很高的精度。

[1]趙國慶.雷達對抗原理[M].西安:西安電子科技大學出版社,1999.

[2]杜龍先.單信道相關干涉儀測向原理[J].中國無線電管理,2000,2(1):41-42.

[3]An Xiaobo,Feng Zhenghe.A signal channel correlative direction finder using VXI receiver[J].International Conference on Microwave and Millimeter Technology Proceedings,2002(3):1158-1162.

[4]趙樹杰,趙建勛.信號檢測與估計理論[M].北京:清華大學出版社,2005.

[5]李淳,廖桂生,李艷斌.改進的相關干涉儀測向處理方法[J].西安電子科技大學學報(自然科學報),2006,33(3):400-403.