基于二代小波變換的電機轉子不平衡故障檢測

范炳奎，李穎暉，柳艷麗

（空軍工程大學 工程學院，西安 710038）

1 引言

1996年，Sweldens和Daubechies提出了提升算法這種新的小波構造方案，被稱為二代小波[1]。與傳統小波從頻域來分析問題的角度不同，二代小波變換完全在時(空)域進行變換，不依賴Fourier變換，小波基函數不再是由某一個函數的平移和伸縮而產生，所有的運算都在時域上進行，不僅能獲得與傳統小波變換同樣的結果，而且實現信號在不同頻帶上的分離[2]，具有結構簡單、運算量小、運算速度快、原位運算、不需要額外內存、可實現整數小波變換、逆變換可以直接反轉實現等特點。

電機工作過程中，當電機產生電磁故障、電機轉子不平衡、軸承不對中或軸承損壞等故障時，會產生不同的振動信號，引發不同的噪聲[3]。通過分析這些振動信息，可以進一步了解和掌握電機的運行狀態及電機的健康狀況。傳統的小波分析方法，由于小波基函數與各個尺度逼近信號的局部特征不能很好地匹配，當閾值選擇不恰當時，濾噪效果不佳[4]。尤其當故障發生的初期，故障振動信號比較微弱，傳統的小波分析方法就表現不佳。本文擬采用二代小波對電機振動信號進行變換分析，采用改良的軟硬折衷閾值處理方法對小波系數進行量化處理，重構振動信號，分析重構信號，提取故障特征。研究表明:將第二代小波變換應用到電機突發性轉子不平衡故障檢測中，能夠快速準確地提取其故障特征，提高了檢測的準確性和可信度。

2 二代小波變換原理

第二代小波變換是由Sweldens提出的一種使用提升模式構造小波的方法。提升過程由分裂、預測、更新三部分組成[5]。

（1）分裂

分裂就是把信號分裂成兩個相互關聯的部分，通常根據信號的奇偶性將信號si分解為兩個較小的子集偶數序列 si?1和奇數序列 di?1， di?1也稱為小波集。設信號為si

（2）預測

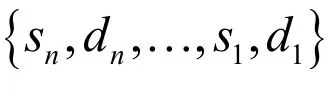
（3）更新

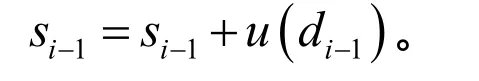
逆變換即重構的過程是分解的逆過程，包括反更新，反預測和合并。

（1）反更新

給定si?1和di?1，可以通過下式恢復偶數序列：

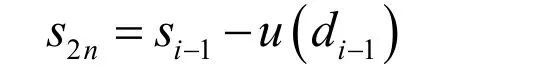
（2）反預測

由反更新得到的偶數序列s2n和給定的奇數序列可以反預測出奇數序列：

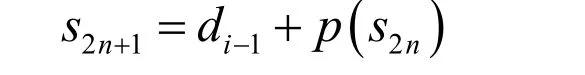
（3）合并

合并反更新的偶數序列s2n和反預測得到奇數序列s2n+1就可以恢復原信號：

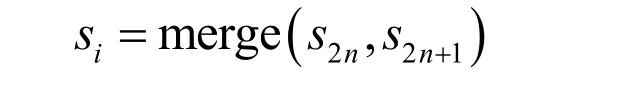
3 基于二代小波變換的電機突發性轉子不平衡故障檢測的原理

電機在工作過程中會發生不同程度的振動。當電機轉子不平衡、滾動軸承異常、滑動軸承異常及安裝、調整不良等都會引起機械振動。當電機轉子質量分布不均勻時，會產生重心位移，引起變化的支撐力，導致電機運行不穩定，從而產生振動。電機轉子不平衡根據現場發生的不平衡特征可以分為三類：（1）短時間停機后產生的不平衡；（2）長時間停機產生的不平衡；（3）運行中突然產生的不平衡。引起轉子突發性失衡原因主要有: 動靜碰磨；轉子零部件脫落或移位；絕緣收縮造成轉子線圈移位、松動；聯軸器不平衡，負序電流過大引起套箍失去緊力；以及冷卻風扇與轉子表面均勻積垢等。轉子突然失去平衡時的振動頻率與轉速頻率相等，振動幅度隨轉速增高而加大[6]。對于每種類型和規格的電機，在穩定運行時，其振動都具有某種特定的典型特性。當電機轉子出現突發性不平衡時，其振動的振幅、形式和頻譜都會發生變化。基于第二代小波變換的轉子突發性不平衡故障檢測步驟如下：

（1）對振動信號進行二代小波變換，將振動信號分解為新的近似尺度系數si?1和小波系數di?1。

（2）對小波系數進行閾值處理，采用改良的軟硬折衷閾值處理方法[7]，公式如下：

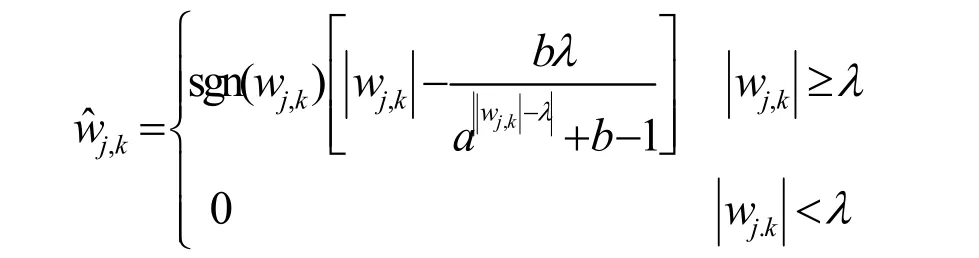
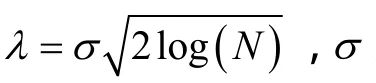
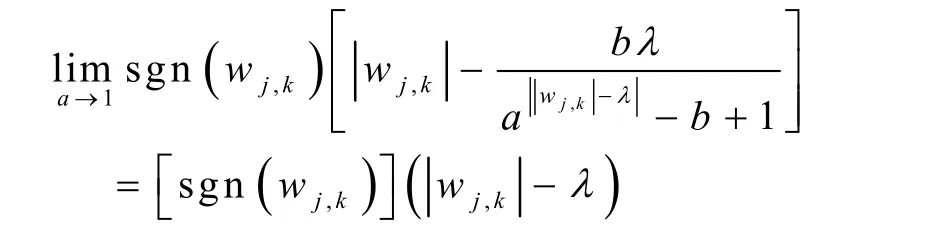
當a→+∞時，表現為硬閾值函數：

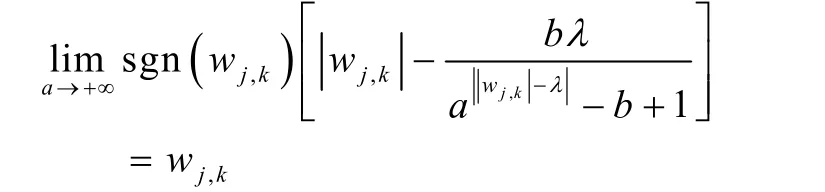
（3）對小波系數 di?1和尺度系數 si?1進行重構，結合轉子突發不平衡時電機振動的特征，分析重構信號得出診斷結果。當重構的信號的振動頻率特性和電機的轉速頻率基本相同時，就可以判斷電機的轉子發生了不平衡故障。

4 仿真試驗

三相異步電動機Y315L-2額定電壓Vn=380V，額定電流 In=365A，額定功率 Pn=200kW，額定轉速ωn=2980r/min，振動為 4.5mm/s，噪聲是 99dB。振動信號如圖1所示。由于信號附有各種噪聲信號，所以從圖1中很難看出信號中包含周期成分，更不能確定周期成分的周期。其信號功率密度譜如圖2所示。

先用傳統小波變換對振動信號進行了分析，本文用“sym3”小波對信號進行3層分解并用軟閾值對小波系數進行量化處理，采樣頻率= 1 000Hz ，重構信號的功率密度譜如圖3所示。

由圖 3可以看出，經傳統小波消噪后的信號高頻噪聲基本被濾除，故障信號的頻率也比較突出，但低頻段消噪效果不理想，干擾故障診斷。尤其在故障發生初期，故障信號相對微弱，傳統的小波分析就難以奏效。為了有效提取微弱信號，試采用第二代小波變換對振動信號進行分解，采樣頻率fs=1000Hz，對振動信號進行四層分解，取a=2000，b=13，對小波系數進行改良軟硬折衷閾值處理，重構尺度系數和小波系數[9]，重構的信號如圖4所示，其功率密度譜如圖5所示。

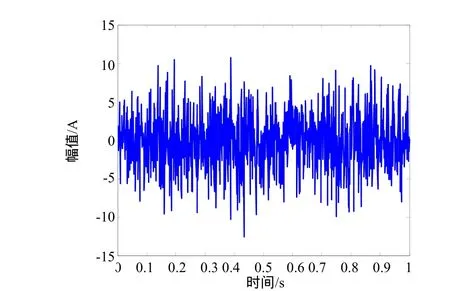
圖1 振動信號波形

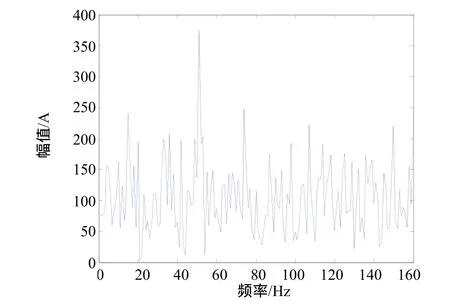
圖2 振動信號功率密度譜圖

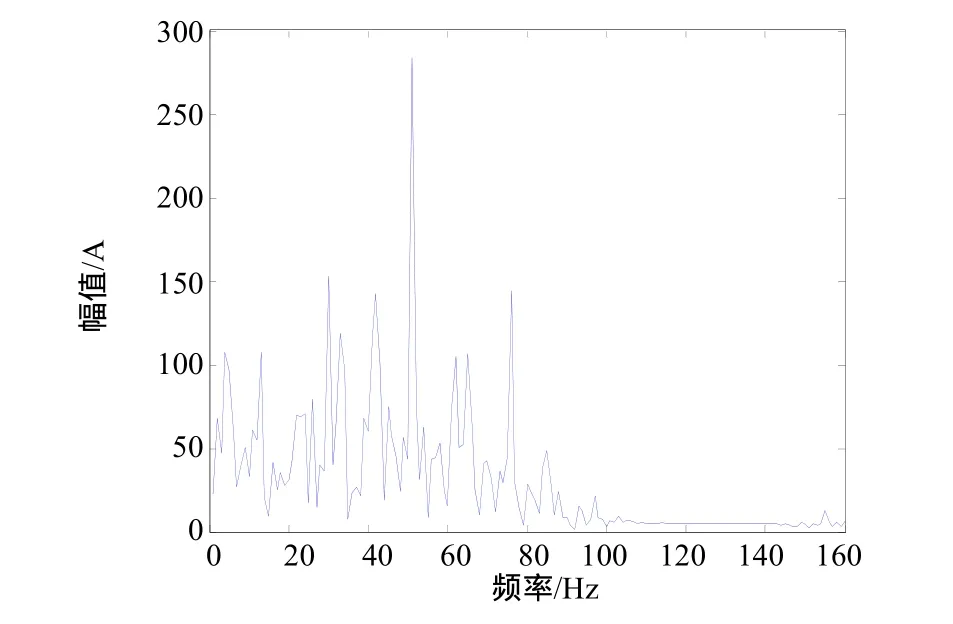
圖3 傳統小波方法重構信號的功率密度譜

由圖5可以知道，第二代小波分析相對于傳統小波分析，其消噪后的信號的故障信號頻率更突出，低頻段消噪效果也比較好，同時濾除了大部分的隨機噪聲，更能準確地提取故障信號的特征，提高了故障信號檢測的可信度。由分析得出的故障信號的頻率大約為 50Hz，電機的轉速頻率為 2980/60=49.7（Hz），參照電機故障特征，可以診斷出電機發生了轉子不平衡故障。

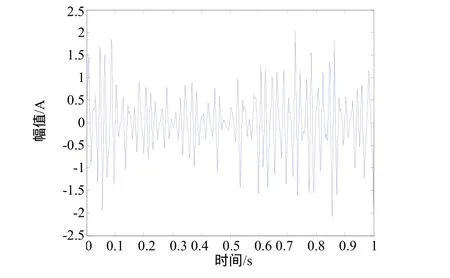
圖4 二代小波方法重構的信號波形

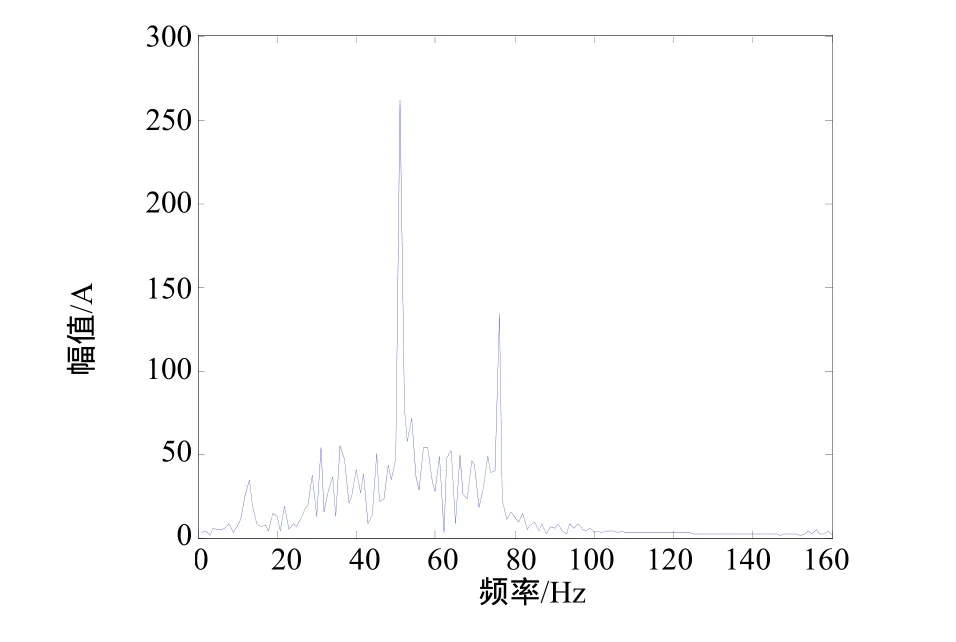
圖5 二代小波方法重構信號的功率密度譜

5 結語

本文基于電機轉子不平衡故障振動信號的特點，提出了用二代小波變換檢測電機轉子不平衡故障的方法。該方法克服了傳統小波變換小波基函數與各個尺度逼近信號的局部特征不能很好地匹配和軟閾值選擇困難的局限性，能夠去除大部分隨機噪聲并準確地提取故障信號特征，尤其是在故障振動信號微弱的故障發生初期，從而及時地發現故障，提高故障檢測的準確性和置信度。但是也存在一些問題，由于第二代小波是利用提升模式構造成的，構造的方案有很多，針對不同研究對象的特點，怎樣選擇最合理的提升方案還需要進一步研究。

[1]Sweldens W. The lifting scheme. A construction of second generation wavelet[J]. SIAM J Math Anal,1997, 29(2): 511-546.

[2]周林成, 楊慧中. 基于二代小波變換的信號去噪及其軟測量建模[J]. 計算機與應用化學, 2008, 25（7）: 823-826.

[3]付華, 尹麗娜. 小波包分解在電機故障診斷中的應用[J]. 微電機, 2007, 40(5):86-89.

[4]劉樹春, 潘紫薇. 第二代小波在振動信號去噪中新方法的研究[J]. 機械傳動, 2008, （4）：64-65.

[5]Daubechies and Sweldens. Factoring wavelet transform into lifting steps[J]. Fourier Anal App,1998, 4(3)：247-269.

[6]王芳，魯順昌. 基于小波包分析的電機故障檢測[J].電機與控制應用，2008，35（7）:52-54.

[7]郭曉霞，楊慧中. 小波去噪中軟硬閾值的一種改良折衷法[J]. 智能系統學報，2008, 3（3）:222-225.

[8]DONOHO D I, JOHNSTONE IM. Adapting to unknown smoothness via wavelet shrinkage[J].Journal of American Stat A ssoc, 1995, 12(90):1200-1224.

[9]高成. Matlab小波分析與應用（第二版）[M]. 國防工業出版社，2007: 210-228.