基于熵權的TOPSIS法配送中心選址方案評價研究

孫洪華， 陳紅霞， 尚 飛 （內蒙古工業大學 機械學院，內蒙古 呼和浩特 010051）

隨著我國經濟發展，企業建立競爭優勢的關鍵，已由節約原材料的 “第一利潤源泉”，提高勞動生產率的 “第二利潤源泉”，轉向建立高效的物流系統的 “第三利潤源泉”。現代物流作為第三種利潤和第三產業的重要組成部分，面臨著前所未有的發展機遇，現代物流快速發展的同時促進了配送中心的建設。目前，國家有關政策的出臺也推動了現代配送中心的進程。商品物流配送自20世紀80年代中后期在我國流通領域出現以來，因其能夠適應社會化大生產專業化分工與協作的要求，減少流通環節、節約流通費用、加快商流和物流速度、實現社會資源的優化配置等特點，受到政府主管部門和流通企業的廣泛重視。國家已明確將發展商品物流配送作為深化流通領域營銷方式改革、實現流通現代化的一項重要內容，并已列入國家流通產業發展規劃。在這兩種因素的驅動下，國內許多行業部門紛紛建立配送中心。對于配送中心的研究也越來越引起人們的注意。國內外的物流實踐證明，發展專業化、社會化的配送中心是現代物流業的發展方向，也是我國傳統儲運業迎接國內外競爭挑戰，向現代物流業轉變的重要途徑。在現代物流網絡中，配送中心不僅執行一般的物流職能，而且越來越多地執行指揮調度、信息處理、作業優化等神經中樞的職能，是整個物流網絡的靈魂所在。因此，發展現代化配送中心是現代物流業的發展方向。

配送中心作為物流網絡的節點，其合理選址不僅影響到配送中心本身的運營成本、運營績效、競爭戰略和未來的發展，而且還影響到配送中心上游的供應商、下游的分銷商或零售商的物流成本、以及物流戰略和競爭戰略，甚至影響到區域經濟的發展。國內外對各種類型物流中心的選址問題在理論和實踐方面都取得了令人矚目的成就，形成了許多可行的模型和方法。歸納起來，這些物流配送中心選址方法分為三類，包括應用連續型模型選擇地點、應用離散型模型選擇地點和應用德爾菲 （Delphi）專家咨詢法選擇地點。

配送中心選址恰當與否，不但對生產力布局、城鎮建設、企業投資、建設速度有重大影響。而且對設施建成后的設施布置以及投產后的生產經營費用、產品和服務質量及成本都有重要的意義。設施選址是一個復雜的技術和社會經濟系統，對其評價涉及的因素很多，其中，有些是可以量化的因素，也有很多定性的因素。在文獻[1]中把需要考慮的因素總結為30種因素，在進行評價方案的時候不一定把30種因素全部進行考慮，可以從其中選擇比較重要的因素進行評價。設施選址的評價標準也已不僅僅局限在成本或運輸距離的最小化，許多定性和定量的因素也影響著企業的決策，因此在進行設施選址的綜合分析比較時，可根據條件采用定性的、定量的或定性定量相結合的方法。設施選址評價屬于多屬性決策評價。常用的設施選址方法有優缺點比較法、加權因素分析法、重心法、線性規劃—運輸法、德爾菲分析模型等。在已有的一些方法中憑主觀經驗進行決策較多。本文根據熵的概念和性質，把熵權引入到設施選址權重確定中，采用多屬性決策理論中的TOPSIS法考慮定性和定量兩種指標對設施選址方案進行評價。

1 TOPSIS法評價原理

TOPSIS（technique for order preferenec by similarity toidel solution）是一種逼近理想解的排序方法[2-3]，它借助多屬性問題的理想解和負理想解對方案集中的方案進行排序。其基本思路是：首先用向量規范化的方法建立規范決策矩陣，然后確定理想解和負理想解，最后計算各方案到理想解和負理想解的距離，根據綜合評價指數對方案進行排序。在應用TOPSIS法時有一個重要的數據即屬性權重的確定，文獻[4]中應用DEA結合AHP方法確定權重，綜合考慮了主觀和客觀的因素。文獻[5]、[6]應用熵權法確定權重。本文中采用熵權的方法給屬性確定權重，熵權法是一種客觀賦權方法，按照信息論基本原理的解釋，信息是系統有序程度的一個度量，熵是系統無序程度的一個度量。如果指標的信息熵越小，該指標提供的信息量越大，在綜合評價中所起作用理當越大，權重就應該越高，權重用如下向量表示。w=（w1, w2,…,wn）T,wi為第i個屬性的權重。

2 基于熵權的TOPSIS法具體算法

步驟1 建立包含n個屬性m個方案的決策矩陣見公式 （1）。

設由n個屬性構成一個指標體系來評價m個方案的優劣，第i個評價對象的第j個指標的值為yij，可以得到各個方案的特征值矩陣為：Y=yij（）m*n。對于給定的j，yij差異越大，則不同評估對象間指標值的相對差距越大，指標對評估對象的比較作用也越大，攜帶和傳遞的信息就越多。

其中Ai是第i個備選方案，Yij是第i個方案關于第j個屬性的數值結果。在n個屬性中有的是效益型指標，記為I1，即指標值越大越好的指標。有的是成本型指標，記為I2，即指標值越小越好的指標，yij∈0,［］1 。另有一些

指標的屬性既非效益型也非成本型指標則需要進行轉換。為消除指標間由于量綱不同而帶來的比較困難使數據能夠在同一個范圍內進行度量，需要對數據進行預處理，把各種類型的屬性范圍轉換為無量綱的屬性，使不同屬性有進行比較的可能。在本文中使用標準0-1變換對決策矩陣Y進行同趨勢化處理：

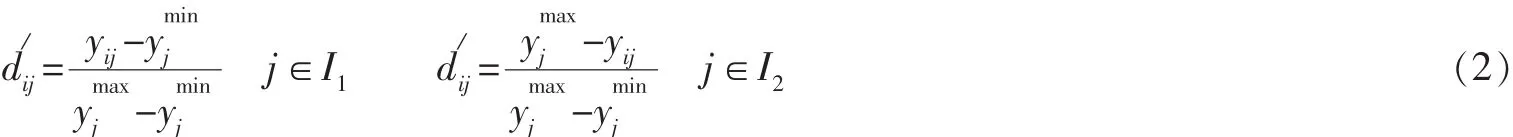
步驟2 用熵權法確定屬性權重。

熵 （entropy）最早由德國物理學家克勞修斯在熱力學中引入，在熱力學中，熵表示物質熱狀態的概率，用來描述離子或分子運動的不可逆現象，是反映自然界熱變化過程方向性的一個物理量，表征物質系統狀態的一個函數。后來應用于信息論中，用熵表示事物或問題的不確定性，誕生了信息熵的重要概念，這為決策定量化開辟了新的道路。在信息論中，信息是系統有序程度的一個度量，熵是系統無序程序的一個度量，二者絕對值相等，符號相反。按照熵的思想，人們在決策中獲得信息的多少和質量是決策的精度和可靠性大小的決定因素之一。熵在應用于不同決策過程的評估時是一個很理想的尺度，不確定性越小，熵值也就越小，反之，熵值就大。按照熵權理論的思想，決策者在決策中取得信息的數量和質量，決定了所制定決策精度和可靠性。

第j項指標的熵為：

計算指標差異度：

計算熵權：

從以上公式可以看出熵權具有以下性質，當di1=di2=…=din時，熵值Hj達到最大值，此時的熵權等于零，也就是說第j個指標沒有向決策者提供任何有用的參考信息，因此該指標可以刪除。熵指標值越大，其熵權越小，該指標就越不重要。從信息的角度考慮，熵權代表該指標在問題中提供有用信息量的程度。所以，計算出的熵權可以作為屬性權重，熵權越大，權重越大，對應指標屬性就越重要。

步驟3用向量規范化的方法求得規范決策矩陣。通過下面的公式把決策矩陣Y=yij｛｝轉化為規范化決策矩陣

步驟4構成加權規范陣X=xij｛｝。

步驟5 確定理想解x*和負理想解x0。

設理想解x*的第j個屬性值為x*

j，負理想解x0的第j個屬性值為x0j，則

步驟6 計算各方案到理想解與負理想解的距離。

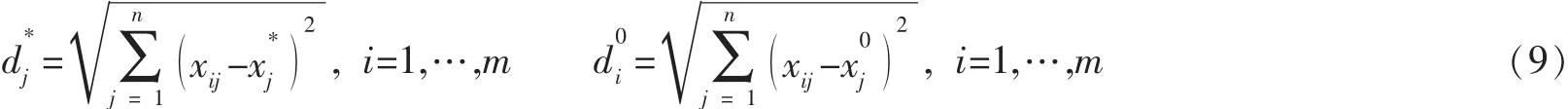
步驟7 計算各方案的綜合評價指數，按綜合評價指數由大到小排列方案的優劣次序。

3 配送中心選址算例

內蒙古某企業由于生產能力擴張，為了進一步發展業務，要新建一個配送中心。考慮經濟、社會、技術等相關因素準備在4個備選場址中進行選擇。備選方案表示A=（A1,A2,A3,A4），評價這4個工程項目考慮5種特征屬性： 指標屬性表示為Y=（Y1,Y2,Y3,Y4,Y5）， 總投資 （Y1單位萬元 ）， 對社會的影響 （Y2基于語義定義 ）， 運行費用（Y3單位萬元/年），內部收益率（Y4% ），凈現值 （Y5單位萬元 ）。對社會的影響是定性指標，要把它定量化，在本例中應用5位專家打分法對4種方案進行分值在［10,20 ］分的打分，綜合5位專家分值取得4種方案平均值為

［15,12,18,14 ］。其中Y1,Y2,Y3為成本型指標，Y4,Y5為效益型指標，決策矩陣如下：

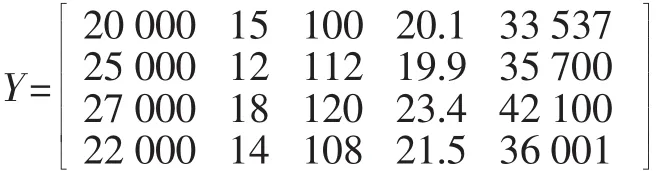
應用公式 （2）、 （3）對矩陣Y進行趨勢化和歸一化處理得矩陣D：

應用公式 （4）、 （5）、 （6） 計算指標的熵權wj：

夏昕鳴，博士生，主要研究方向為經濟地理、投資與區域經濟；李芬，經濟學博士，研究員，方向為環境政策管理、生態城市規劃。

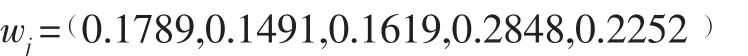
用向量規范化的方法求得規范決策矩陣。通過公式（7）把決策矩陣Y=yij｛｝轉化為規范化決策矩陣Z=zij｛｝。

應用公式 （8）構成加權矩陣X：

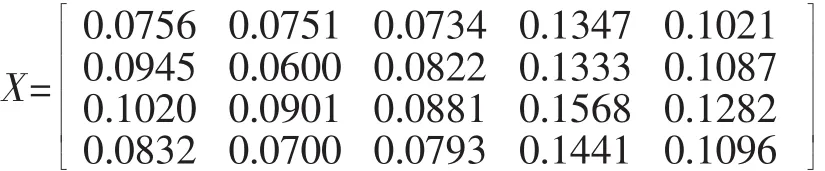
確定理想解x*和負理想解x0，Y1,Y2,Y3為成本型指標，Y4,Y5為效益型指標，在成本型指標中理想解選擇越小越好，在效型指標中理想解選擇越大越好。

根據公式 （9）計算各方案到理想解與負理想解的距離：

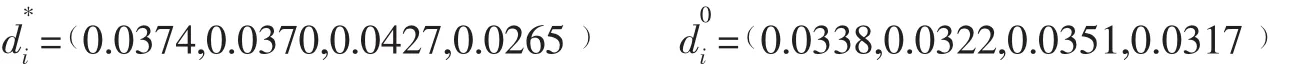
根據公式 （10）計算綜合評價指數C*

i

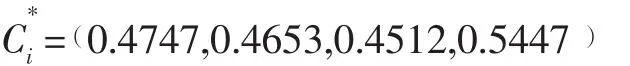
按綜合評價指數由大到小排列方案的優劣次序為A4優于A1優于A2優于A3。

4 結 論

對多屬性配送中心選址決策問題： （1）充分考慮各指標權重的影響，引入歐式距離，使評價結果更精確。（2）應用改進的TOPSIS法對配送中心選址方案進行評價。它通過對原始數據進行同趨勢和歸一化，可消除不同量綱的影響，應用歐式距離度量每個方案與正、負理想解得距離，并通過計算每個方案的綜合評價指數對方案優劣進行排序。實際應用例子說明，該方法的決策原理簡單、易于實現，為該領域的評價方法提供了新的思路。

[1] 朱耀祥，朱立強.設施規劃與物流[M].北京：機械工業出版社，2004:102-103.

[2] 岳超源.決策理論與方法[M].北京：科學出版社，2003:212-214.

[3] 陳廷.決策分析[M].北京：科學出版社，1987:203-206.

[4] 王旭，陳嘉佳，邢樂斌.基于 “TOPSIS/DEA/AHP”模型的戰略性供應商選擇[J].工業工程，2008,11(4):70-73.

[5] 何鑫，朱宏泉，高成鳳.基于熵權法與TOPSIS法的房地產項目投資風險評價[J].商業研究，2009(3):105-108.

[6] 羅建強，韓玉啟，張銀萍.基于熵權TOPSIS的客戶訂單分離點定位研究[J].工業工程與管理，2008(5):83-87.

[7] 趙遠飛，陳國華.基于改進逼近理想解排序 （TOPSIS）法的應急系統優化選址模型研究[J].中國安全科學學報，2008(9):22-28.