二維混凝土骨料類型的數值模擬

□文/邵海成 周立明 胡建強 項利南

對于三級配或全級配混凝土，濕篩法導致混凝土的組成比例發生了變化，尤其水泥砂漿和骨料含量的比例，因此試件的力學性能不同于實際情況下的力學性能。通過試件確定的所有力學指標都不能真實反應實際結構的力學指標，在結構的設計和施工中將出現不精確性。因此，結合一定數量的試驗，需要通過使用微級數值模擬方法來研究大體積混凝土的性質。

混凝土的數值模擬主要集中在骨料形狀的模擬上。建議采用幾種模型來預測混凝土的性質。第1個是隨機骨料模型，這個模型經常用來模擬固體顆粒材料；第2個模型是隨機填充顆粒模型，它是用來模擬波特蘭水泥混凝土的；第3個是一個隨機二維天然形狀骨料模型，它為混凝土數值模擬的進步做出了巨大貢獻；第4個是網格模型，由于計算能力的不精確性它并沒有投入實際應用；第5個是梁-顆粒模型，該模型是由在離散元法的基礎上開發出來的。

為了得到更多的混凝土的真實特性，采用一個更精確的方法來模擬骨料形狀是非常必要的。

生成任意多邊形的算法

任意三角形的生成

首先同時設置相同直徑的任意排列圓形，用來控制三角形基本骨料的尺寸和位置。骨料的直徑決定圓形的半徑。三角形基本骨料的生成是建立在這些任意排列的圓形的基礎上。方法描述如下：

（1）在每個圓形的輪廓線上隨機的生成3個點；

（2）在動態三角形中，通過控制角度的余弦值來生成一個銳角三角形。

然后，根據三角形基本骨料可以生成任意多邊形骨料，見圖1。任意三角形基本骨料決定了骨料的直徑和最終幾何形態。

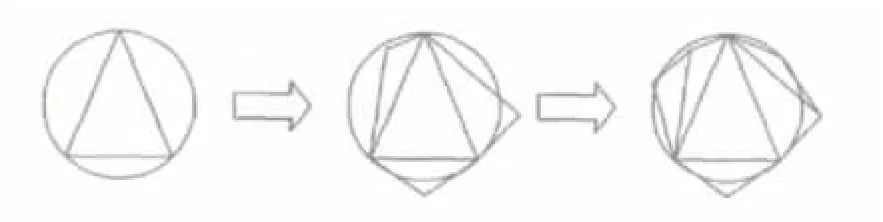
圖1 三角形骨料的任意延伸

延伸條件和方法

多邊形的延伸條件：有一個邊，它的長度至少要大于極限值Lmax。在以這條邊為直徑的半圓中生成一個新的頂點p，如圖2所示。p的坐標計算如下：

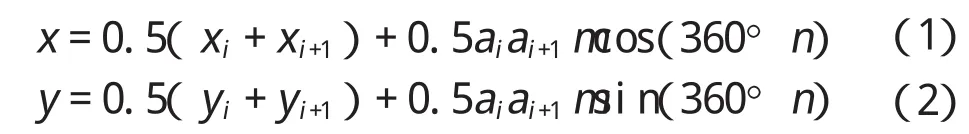
式中：m和n分別表示0～1的隨機數字。在公式（3）中如果S＞0，則p位于半圓內側。如果S大于三角形aiai+1p′的面積，那么p將不會位于三角形aiai+1p′的內側并且多邊形的形狀將接近于實際骨料形狀。見圖2。三角形aiai+1p′的面積計算

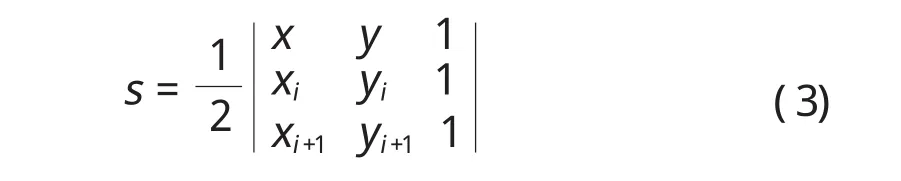
通常情況下，實際骨料經常顯為凸形。因此，本文中的算法也受限于骨料的凸形。由于這個限制，p將限制于2倍基本骨料直徑的距離之內。為了確定兩個顆粒之間是否存在重疊，唯一要做的是：確定兩個相鄰圓形中心之間的距離。如果這個距離大于2倍的直徑，那么兩個顆粒還沒有彼此重疊。由于沒有必要一一確定這個條件，所以這樣很大程度上提高了效率。

多邊形的重疊準則

角度之和的計算

分別連接p和a1,a2,…,an。θi表示∠aipa+（1i=1，2，…，n-1），表示。如果表示p位于多邊形a1,a2,…,an外，見圖 3a；如果，表示p位于多邊形a1,a2,…,an內，見圖3b，其中通過余弦定理可以計算θi，它的正負定義如下，以∠a1pa2為例。

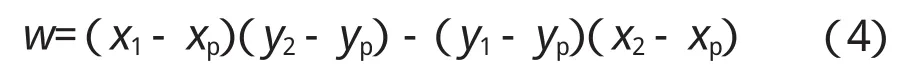
如果w＜0，角度的方向為順時針，則θi是負的；相反如果w＞0，角度的方向為逆時針，則θi是正的。

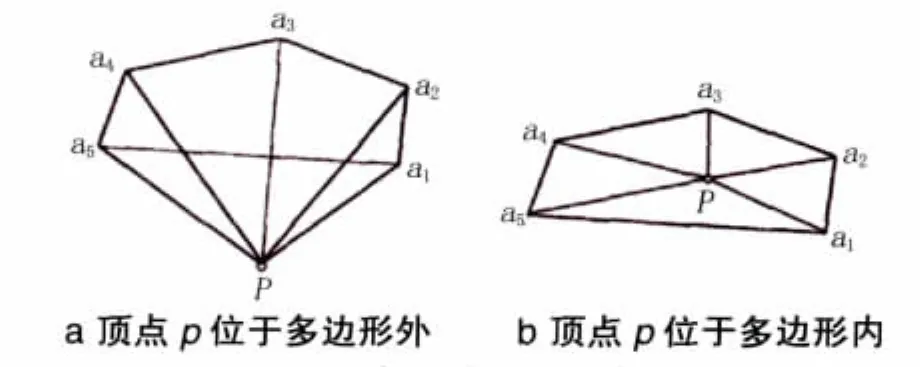
圖3 p與多邊形之間的關系

檢測相交

為了避免特殊情況，如圖4所示，有必要確定兩條邊是否相交。通過分別連接p和ai、ai+1，可以使每條直線有兩個方程。當這些方程中的每一個都結合了直線a1a2,a2a3,a3a4,a4a5和a5a1的方程中的一個時，通過使用克拉默法則就可以獲得交點的坐標，然后就可以給出這個點是否在骨料輪廓線上的判定標準。

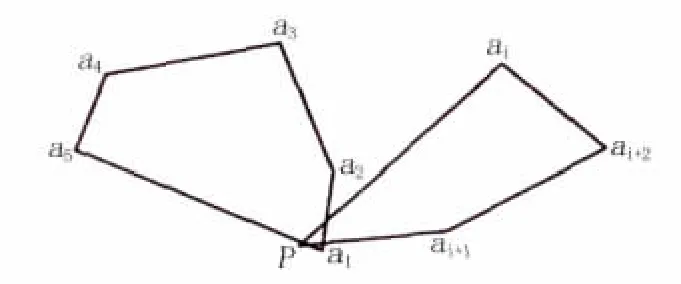
圖4 兩個多邊形相交的特殊情況

凸度條件

對于任意多邊形，確定多邊形的凸度是一個臨界控制條件。這個條件可以確保p將不會無限制的延長。因此在這個算法中必須提供凸度條件，使（x1，y1），（x2，y2）和（x3，y3）分別成為某個特定三角形 3個頂點的坐標，這些點以逆時針順序排列，然后三角形的面積可以表示

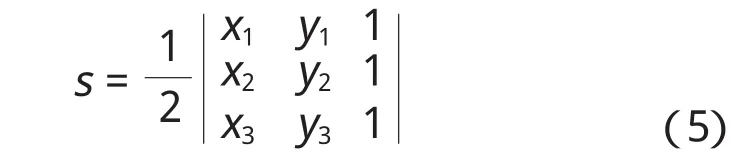
如圖5所示，在這些已有邊的條件下插入p來形成多邊形的新邊。凸度條件是三角形的面積受制于點p和對邊，基于公式（5）邊ai-1ai或ai+1ai+2必須是正的。

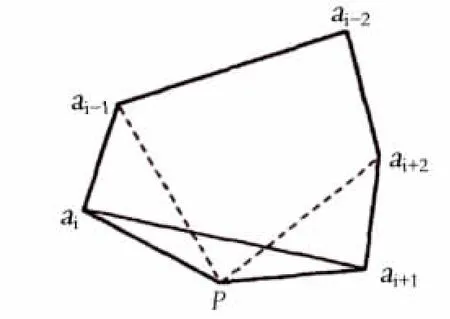
圖5 三次延伸后新的頂點p

骨料交界面的生成

本文交界面生成的方法不同于在盤狀顆粒中使用的方法，對于交界面，在此方法中限制了兩個相鄰顆粒中心間更長的距離，以此來預留空間。在現有的方法中首先生成大骨料，然后標定它的尺寸來形成交界面，見圖6。根據相似三角形原理就很容易計算骨料所有頂點的坐標。

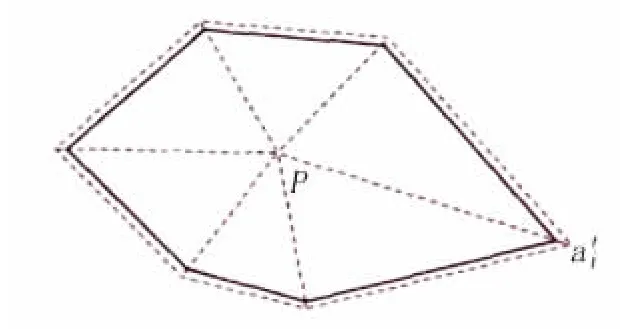
圖6 骨料的交界面

2D-RAS的主要步驟

（1）根據骨料含量和一種級配骨料的平均直徑，計算骨料的數量。

（2）生成所有隨機數字來確定所有骨料的位置，然后將所有的基本骨料一次安放于混凝土截面。

（3）檢查所有基本骨料的重疊部分。如果沒有重疊部分，則進行步驟4，否則重復步驟2和3。

（4）為每個基本骨料生成延伸骨料。任意骨料的生成也需要檢查重疊和交叉的條件。

（5）對于下一級配，重復上述步驟，從而生成全級配混凝土（或三級配混凝土）的模型。

使用軟件2D-RAS生成了骨料含量為65%的任意骨料模型，見圖7。

圖7 骨料含量為65%的隨機骨料模型

數值算例與討論

非線性本構模型

考慮到準脆性材料的破壞并不是完全脆性，而是在達到極限強度后顯示出一些延展性。事實上，在開裂末端前存在一小區域，而正是在此區域發生微裂縫的發展和聚結。本文將使用準脆性破壞本構模型來模擬砂漿和交界面的開裂破壞，該模型由內聚力可以表示如下

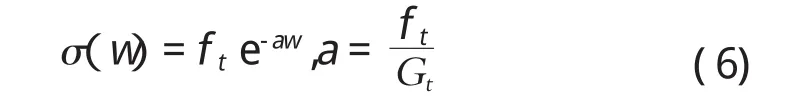
式中：f t表示材料的極限強度，Gt表示開裂能。骨料被看做線彈性材料。開發了有限元軟件ABAQUS，用以執行一系列數值分析。在這個計算中，為復合材料的每一相都運用了非線性本構模型，見圖8。

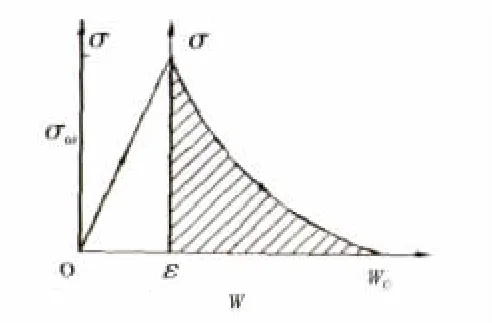
圖8 材料的本構模型

三級配混凝土的單軸拉伸試件

隨機骨料模型

本文中所研究的試件的尺寸為450 mm×400 mm，見圖9。由軟件2D-RAS生成的隨機多邊形骨料模型見圖10a，圖10b所示為隨機盤狀骨料試件。兩個模型具有相同的骨料含量。表1中給出了計算中所采用的材料參數。

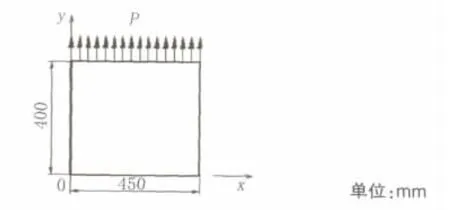
圖9 試件的幾何尺寸和荷載作用

圖10 破壞時裂縫的傳播和開裂模式

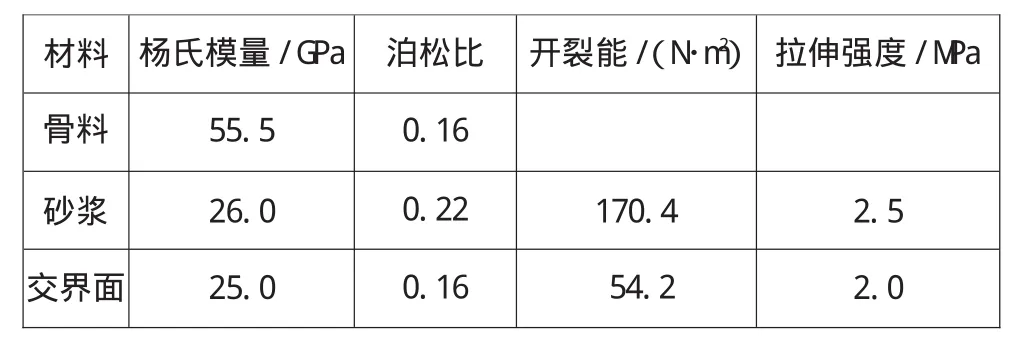
表1 分析中所采用的材料參數

結果和討論

通過位移來控制拉伸荷載，從而模擬軟化階段混凝土的非線性材料影響。由于應力集中現象非常明顯，在任意多邊形骨料的混凝土試件中將很早就出現裂縫。這些試件中，在一個骨料的交界面單元將首先發現微裂縫，因為它的極限強度低于砂漿的強度。當荷載增加時，交界面出現了越來越多的破壞單元，而且在砂漿中也發現了一些破壞單元。最后，通過連接破壞單元而形成一條宏觀裂縫，從而導致試件完全破壞。

多邊形骨料試件計算的極限拉伸強度是1.61 MPa，而盤狀骨料試件計算的極限拉伸強度是1.66 MPa，見圖 11。

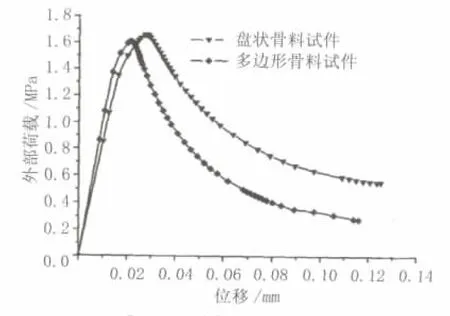
圖11 荷載—位移曲線

任意多邊形試件的結果明顯比盤狀顆粒試件的結果更接近試驗結果。與多邊形骨料試件相比，盤狀骨料試件的極限荷載要大3%。

三級配混凝土的彎曲試件

隨機骨料模型

這部分給出的例子是尺寸為300 mm×1 100 mm的一個彎曲單一支持梁，粗、中、細骨料的代表直徑分別為60、30、12.5 mm。三級配混凝土大、中、小骨料的比例為4∶3∶3。骨料的密度為2.8×103kg/m3。梁的中間部分（尺寸為300 mm×200 mm）為多相復合材料。大顆粒盤狀骨料、中顆粒盤狀骨料、小顆粒盤狀骨料的數量分別為3、10、68。當任意形狀多邊形模型生成之時，大骨料、中骨料、細骨料的面積分別為7 800、6 780、8 400 mm2。兩種隨機骨料模型均由2D-RAS軟件生成。在分析中每相所采用的材料參數（除了兩端混凝土的彈性模量和泊松比分別為30.0 GPa和0.17）也與第一個例子中所采用的材料參數相同。混凝土中的材料（骨料）也被認為是線彈性材料。兩種情況下的骨料級配和含量也都相同。

結果與討論

兩種情況下每個試件的極限荷載見表2。盤狀骨料混凝土梁的極限荷載大部分都大于多邊形骨料混凝土梁的極限荷載；唯一的例外就是第二部分數值模擬試件。前者的平均值大于后者的平均值為4%。

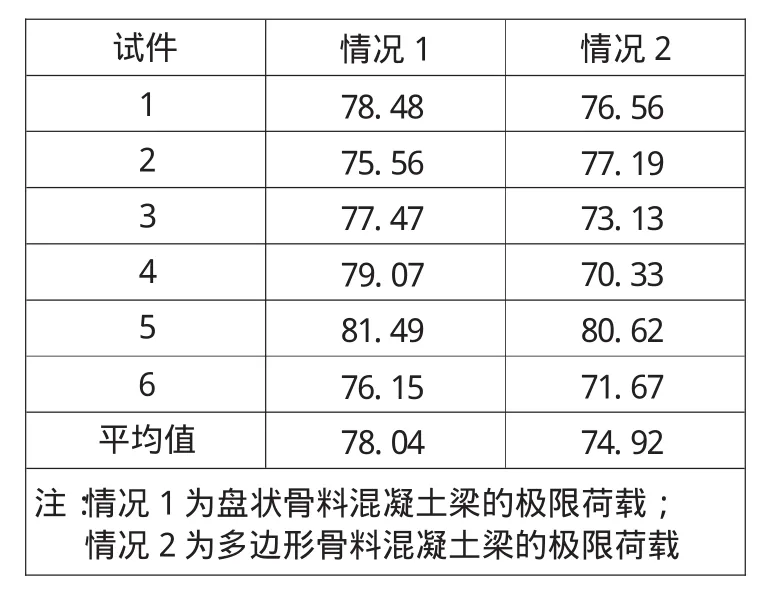
表2 試件的極限荷載 kN

結果表明任意多邊形骨料混凝土梁的裂縫深度大于盤狀骨料混凝土梁的裂縫深度，而且前者的裂縫數量也多于后者，見圖12。

圖12 破壞時試件裂縫的傳播過程和開裂模式

結論

（1）本文研究的算法（用至少5個隨機數字來定義一個任意形狀骨料）要優于現存的盤狀顆粒骨料算法（用2個隨機數字來定義一個盤狀顆粒骨料）。由本文研究的算法所生成的骨料形狀更接近于實際情況。

（2）與現存的算法相比，本文研究的算法要優于其他算法。該算法通過隨機生成的圓形區域來同時為骨料定位，僅僅相鄰的骨料需要判斷是否相交，這樣可以大大提高算法的效率。由2D-RAS生成的骨料含量可以高達65%，這幾乎是三級配或全級配混凝土的實際骨料體積比。

（3）數值模擬的例子表明多邊形骨料的單軸拉伸試件和彎曲試件的極限荷載要低于盤狀顆粒骨料的單軸拉伸試件和彎曲試件的極限荷載。

［1］高政國，劉光廷.二維混凝土隨機骨料模型研究［J］.清華大學學報（自然科學版），2003，43（5）：135-139.

［2］馬懷發，陳厚群，黎保琨.混凝土試件細觀結構的數值模擬［J］.水利學報，2004，（10）：27-35.

［3］孫立國，杜成斌，戴春霞.大體積混凝土隨機骨料數值模擬［J］.河海大學學報（自然科學版），2005，33（3）：291-295.