高速圓柱滾子軸承柔性保持架的動力學分析

李 晌，蔣新力，姜艷紅，梁 波，鄧四二

（1.河南科技大學 機電工程學院，河南 洛陽 471003；2.洛陽LYC軸承有限公司，河南 洛陽 471039；3.洛陽軸研科技股份有限公司，河南 洛陽 471039）

高速圓柱滾子軸承在高速輕載條件下工作時，滾子法向受載很不均勻，會出現較大的非承載區。這時，在整個周向上滾子的運動速度會產生很大波動，進而導致滾子和保持架發生碰撞，這種保持架的動態不穩定性是造成軸承零件失效的一個關鍵因素，因此對軸承零件進行精確的動力學分析顯得尤為必要。文獻［1］用6自由度模型研究了滾子軸承保持架的不穩定性；文獻［2-3］研究了套圈為柔性體的滾子軸承保持架的動力學特性，分析了剛柔耦合產生的影響；文獻［4-5］建立了滾子軸承動力學模型，可以計算各零件間的載荷分布及動態模擬保持架的打滑；文獻［6］對航空發動機主軸承中保持架的振動特性進行了分析。到目前為止，大多數的研究都把軸承整體視為剛性體，軸承的變形僅限于各零部件間接觸部位的彈性變形，計算結果精度有限，并不能真實地反映軸承的實際運動狀態。

航空發動機主軸承保持架的過梁較薄，剛性較差，柔性較大，工作中易產生彈性變形。這里，在柔性多體系統動力學的理論基礎上，將保持架視為一個柔性體，研究其變形與軸承整體剛性運動的相互作用或耦合，分析航空發動機主軸承的動態特性［7］。

1 虛擬樣機的建立

ADAMS對含有柔性體的機械系統進行仿真的過程為：加載ADAMS／AutoFlex模塊，計算并調入模態中性文件至ADAMS／View中，創建柔性體并建立剛柔耦合模型，然后運用ADAMS／View中提供的約束將柔性體與模型中的其他零件連接起來，最后根據仿真要求，對柔性體進行參數設置，完成仿真并分析仿真結果。這里，在ADAMS／AutoFlex模塊中計算出保持架的mnf文件后，導入ADAMS／View完成保持架為柔性體的剛柔混合建模，通過啞物體為保持架和其他零件建立連接，最后在軸承各零件間建立約束作用力。

圖1為圓柱滾子軸承剛柔耦合模型，其中含有細線狀一維均布單元的零件為柔性保持架，其余零件為剛性體。

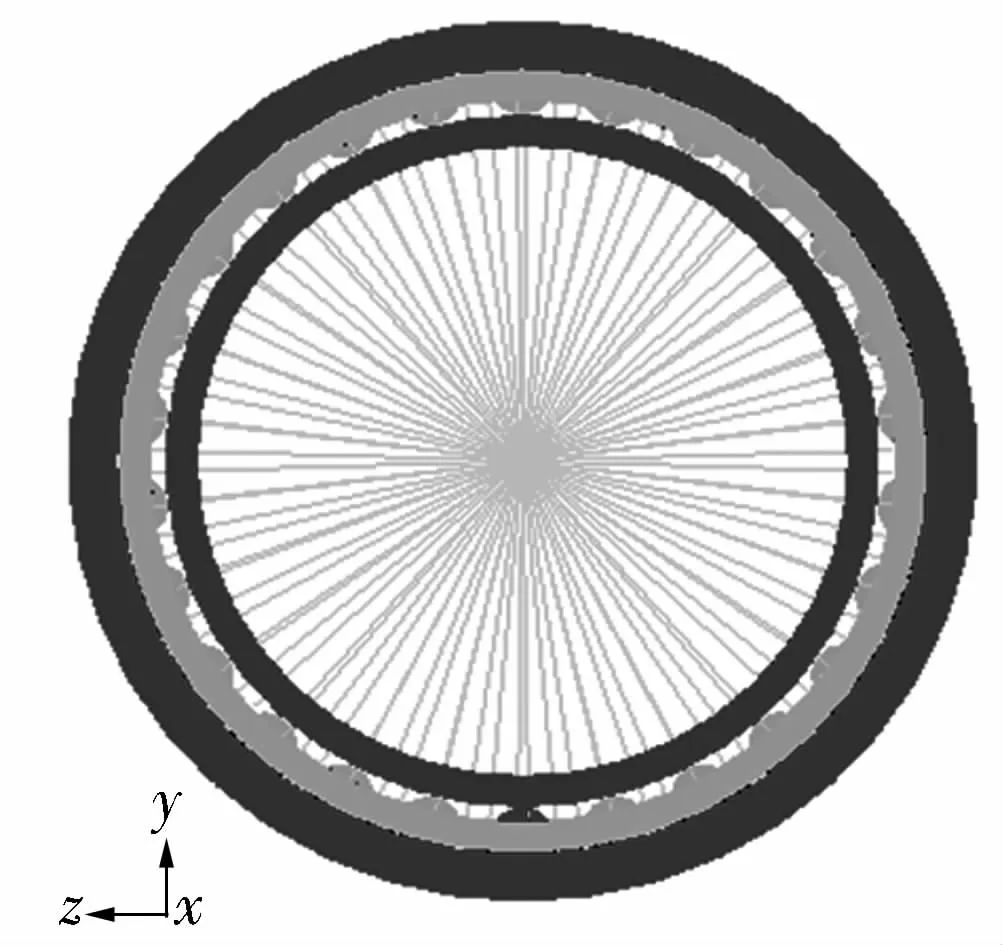
圖1 剛柔耦合模型

2 軸承內部相互作用力模型

滾動軸承的內部作用力非常復雜，不僅存在固體與固體間的相互作用，還存在著固體與液體間的相互作用。假設套圈和滾子具有良好的剛性，幾何變形僅存在于局部接觸部位，滿足Hertz接觸理論。由于考慮速度問題，在計算油膜拖動力時，采用中心油膜厚度。軸承內部各零件間相互作用力模型如圖2所示。

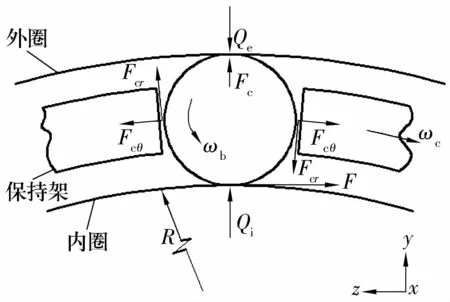
圖2 軸承內部作用力模型

2.1 滾子和套圈之間的作用力

2.1.1 法向力

根據Palmgren線接觸公式，彈性變形量計算式為［8］：

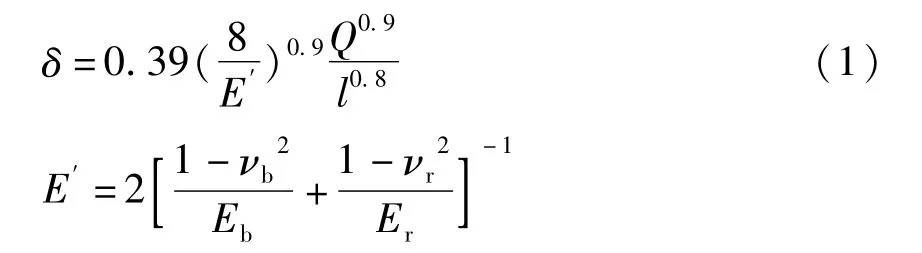
式中：E′為等效彈性模量，mm2／N；Eb，Er分別為滾子和套圈材料的彈性模量，N／mm2；νb，νr分別為滾子和套圈材料泊松比；Q為法向接觸載荷，N；l為接觸長度，mm。

考慮滾子凸度及滾子傾斜的影響，采用切片法，根據每個切片變形δ計算切片受力，再對其求和得到滾子的法向接觸力Q。

2.1.2 摩擦力的計算

接觸區摩擦或拖動系數μ隨潤滑狀態的不同而改變，計算方法類似文獻［9］：

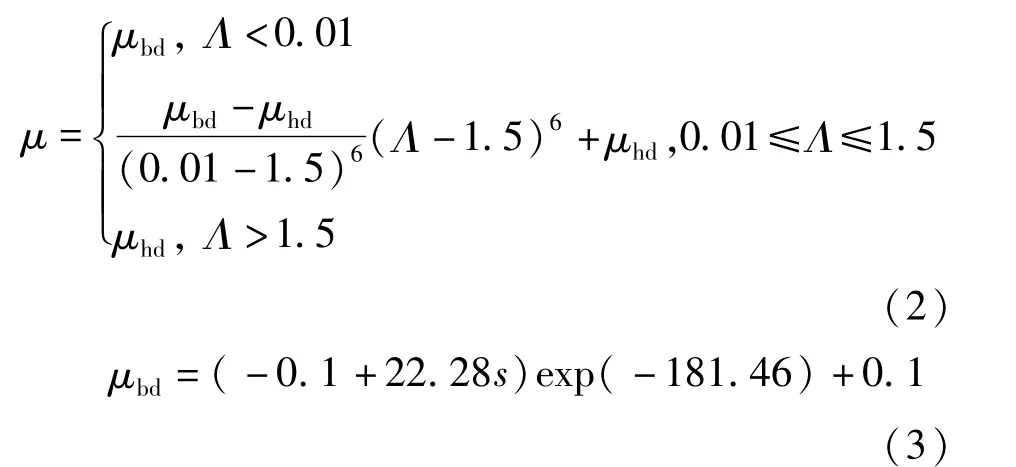
式中：μbd為邊界摩擦系數；μhd為油潤滑時的拖動系數，由文獻［10］的回歸經驗公式求得；Λ為油膜參數，其值為接觸區中心油膜厚度與接觸表面綜合粗糙度之比；s為滑滾比，s＝（v1-v2）／v，v1，v2分別為接觸處滾道和滾子的線速度，v＝（v1＋v2）／2。

摩擦力F為：

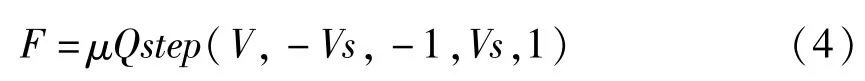
式中：step函數是ADAMS提供的階躍函數，當摩擦速度非常小或瞬時發生反向運動時可去除摩擦力的不連續性，保持摩擦系數不發生突變。

接觸區中心油膜厚度為［11］：

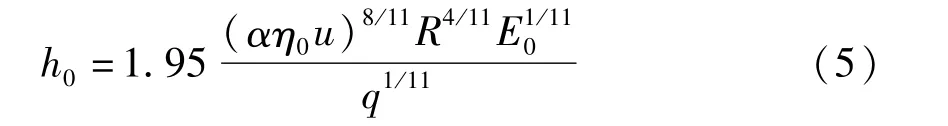
式中：α為黏度的壓力指數；η0為常壓下油的動力黏度；u為滾子圓周表面平均速度；R為當量曲率半徑；E0為當量彈性模數；q為單位接觸長度上的載荷。

2.2 滾子和保持架之間的作用力

滾子對保持架的作用力推動或阻礙其運動，加之黏性阻尼的存在，計算非常復雜。這里，主要采取速度控制模型來求解滾子與保持架兜孔間的作用力［12］。在該模型中，滾子與保持架間法向作用力與其中心距成比例，而中心距由相鄰滾子的公轉速度和保持架的速度差決定。保持架的轉速取所有滾子公轉速度的平均值。在某一具體位置，滾子對保持架的法向作用力Fcθ為：

若滾子在兜孔中心位移超過兜孔間隙，則用Hertz理論來計算此作用力。

2.3 保持架和套圈間的作用力

航空發動機主軸承多采用外圈引導，保持架和套圈之間的作用力是指引導擋邊與保持架外圓柱面之間的流體動壓力。因二者之間作用面較小，該作用力常采用短滑動軸承理論進行計算［13］。保持架與引導面之間作用力如圖3所示。

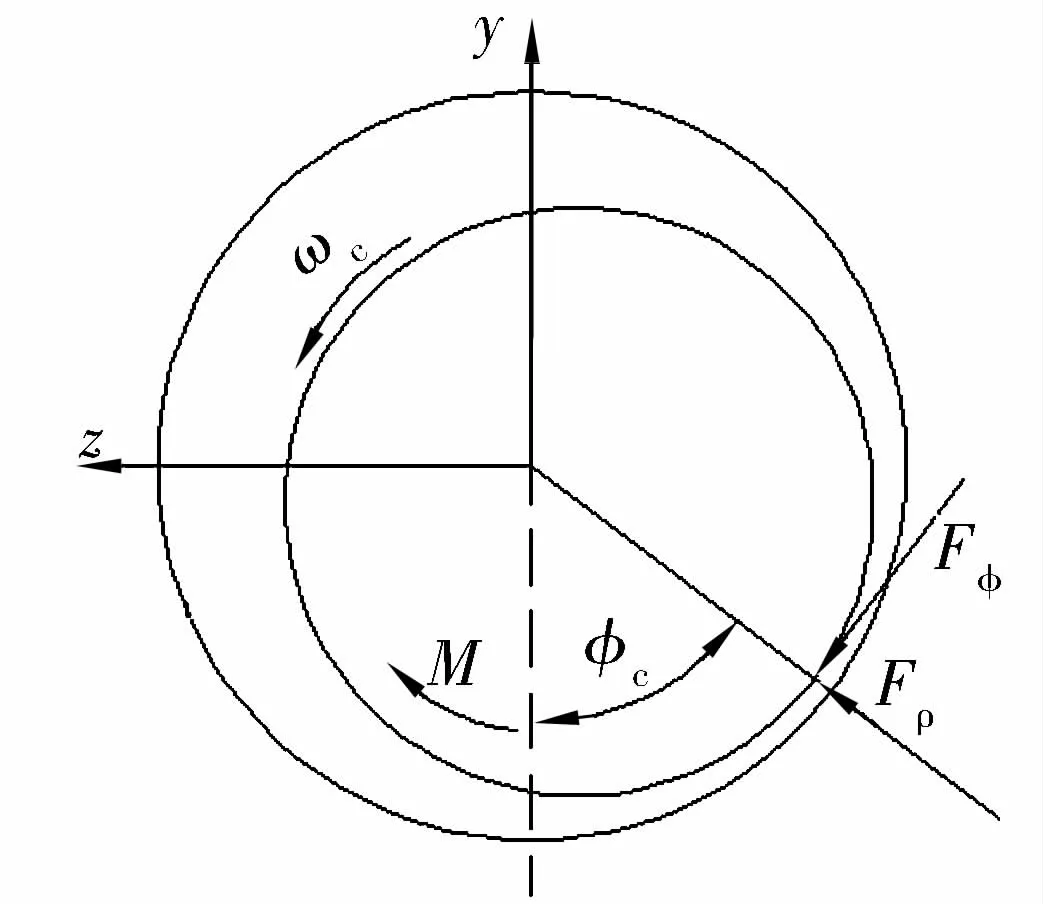
圖3 保持架與引導面作用力

在保持架平面內作用力的合力和力矩為：

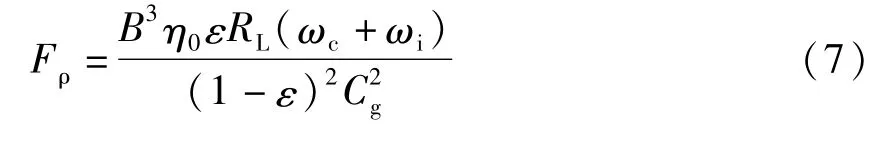
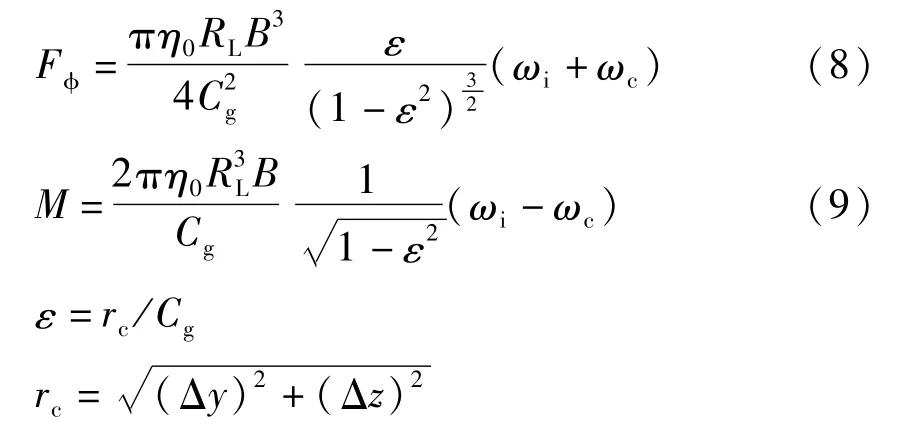
式中：RL為引導面半徑；B為引導面寬度；Cg為引導面間隙；rc為保持架質心偏移量；Δy，Δz為保持架在y，z方向的質心位移；ωi為引導套圈的轉速；ωc為保持架轉速；η0為油膜動力黏度。

由圖3可知，作用力合力與保持架整體坐標系之間有一偏角?c，因此需將上面的力轉化到該整體坐標系中，即：

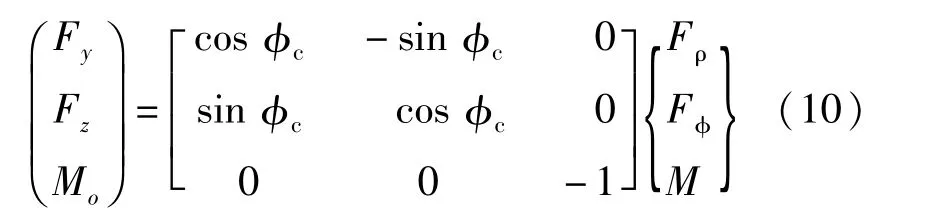
2.4 保持架運動微分方程

在研究多柔體系統時，合理的坐標系是非常重要的。對柔性保持架，選擇廣義坐標ζ，ζ＝［RΩq］T，其中R是位移坐標，Ω是Euler角坐標，q為模態坐標。柔性保持架的運動微分方程可由Lagrangian方程導出：

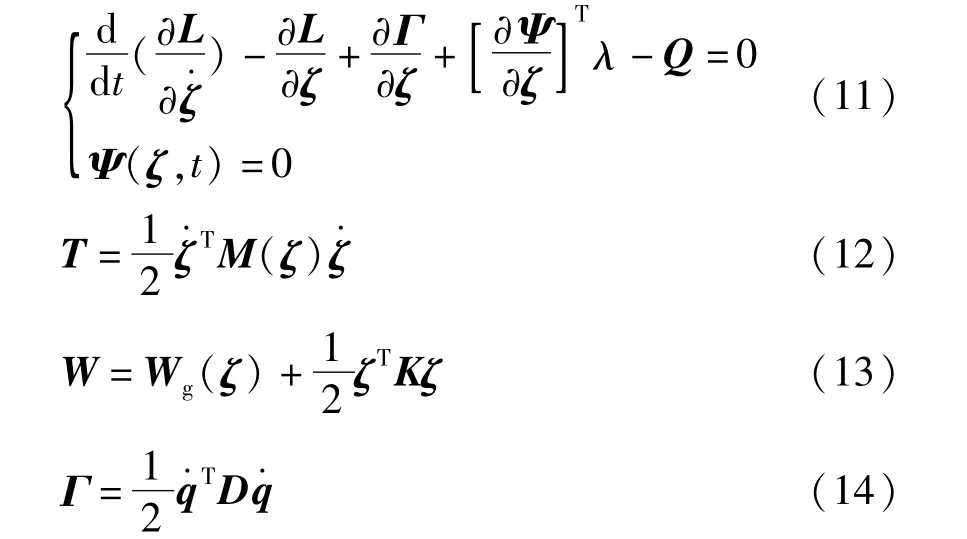
式中：K為對應于模態坐標的部件剛度矩陣，通常為常量；L為拉格朗日項，L＝T-W，T和W分別為動能和勢能；Γ表示能量損耗函數；Ψ為約束方程，一般為廣義坐標和時間的函數；λ為對應于約束方程的拉氏乘子；Q為投影到ζ上的廣義力，Q＝［QT，QR，QM］T，QT為廣義平動力，QR為廣義扭矩，QM為廣義模態力，將保持架所受合外力、外力矩分別通過坐標轉換便可得到柔性保持架的廣義力；矩陣D包含阻尼系數，是常值對稱矩陣；Wg（ζ）為重力勢能項，對其求導即得廣義重力fg；M（ζ）是質量矩陣。

由（11）～（14）式得保持架最終的運動微分方程為：

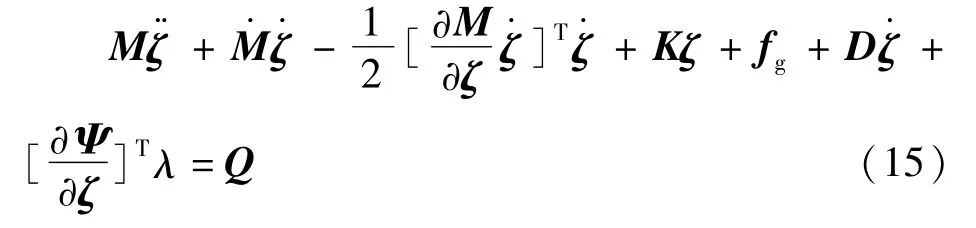
3 軸承的運動仿真

針對某航空發動機主軸承，應用上述模型進行動力學仿真。該圓柱滾子軸承為外圈帶雙擋邊，內圈不帶擋邊，滾子為凸度設計的結構。該軸承幾何尺寸為：d＝100 mm，D＝140 mm，B＝20 mm。該軸承內、外圈同向轉動，轉速分別為：ωi＝1×104r／min，ωe＝1.2×104r／min。該軸承所承受的徑向載荷Fr＝2 kN，使用的潤滑油牌號為MILL-7808G。

3.1 模態識別

這里共計算26階模態，考慮到低階模態的影響，表1列出了保持架前10階模態，前6階為剛體的6個自由度，已被系統取消。由表1可知，模態階數越高，保持架的固有頻率越大，仿真時如發現某階模態對彈性體的影響較小，就可以考慮取消該階模態，這對提高剛柔耦合模型的仿真速度是有益的。

表1 保持架的固有頻率 Hz

通過仿真可知，第12階、20階模態對保持架影響較大，振型如圖4所示。12階模態為保持架在環平面內的彎曲振動；20階模態為保持架在圓周方向上的彎扭耦合振動。這兩種振型會使保持架過梁產生剪切應力，由振動應力產生的疲勞裂紋最易在此處發生。通過優化保持架兜孔參數，提高其抗彎扭能力可有效解決這個問題。

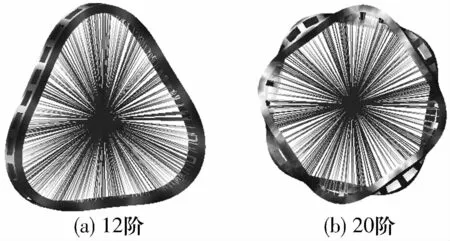
圖4 保持架模態

3.2 徑向載荷對保持架動態性能的影響

圖5為軸承徑向載荷與保持架打滑率的關系曲線。由圖5可知，保持架打滑率隨著軸承徑向載荷的增大而減小。徑向載荷的增大，引起滾子和套圈間的切向拖動力增大，使得滾子和保持架的公轉速度提高，最終使得保持架打滑率減小。

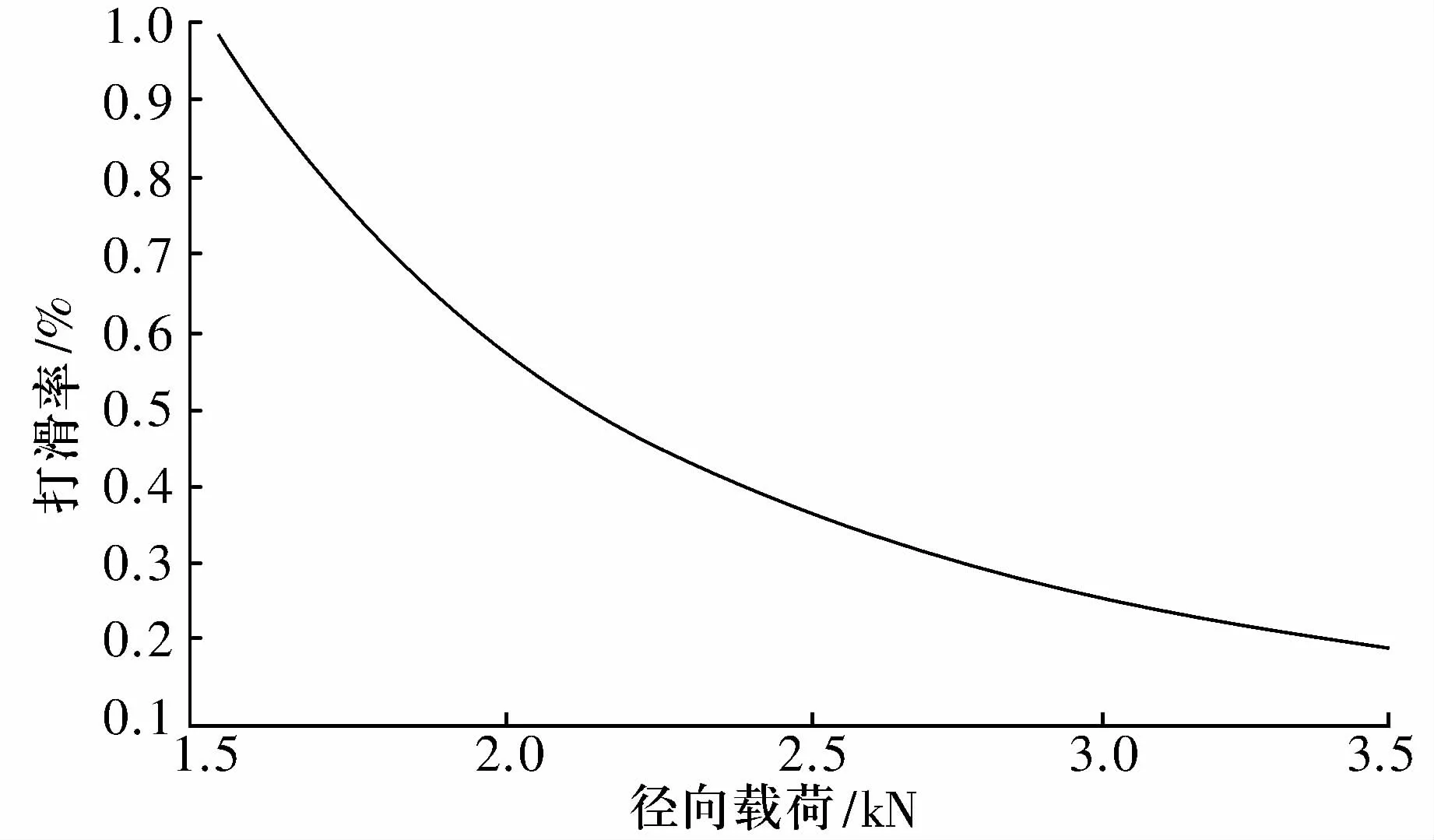
圖5 軸承徑向載荷與保持架打滑率的關系

3.3 徑向游隙對保持架動態性能的影響

圖6為軸承徑向游隙與保持架打滑率的關系曲線。由圖6可知，保持架打滑率隨著軸承徑向游隙的增大而減小。

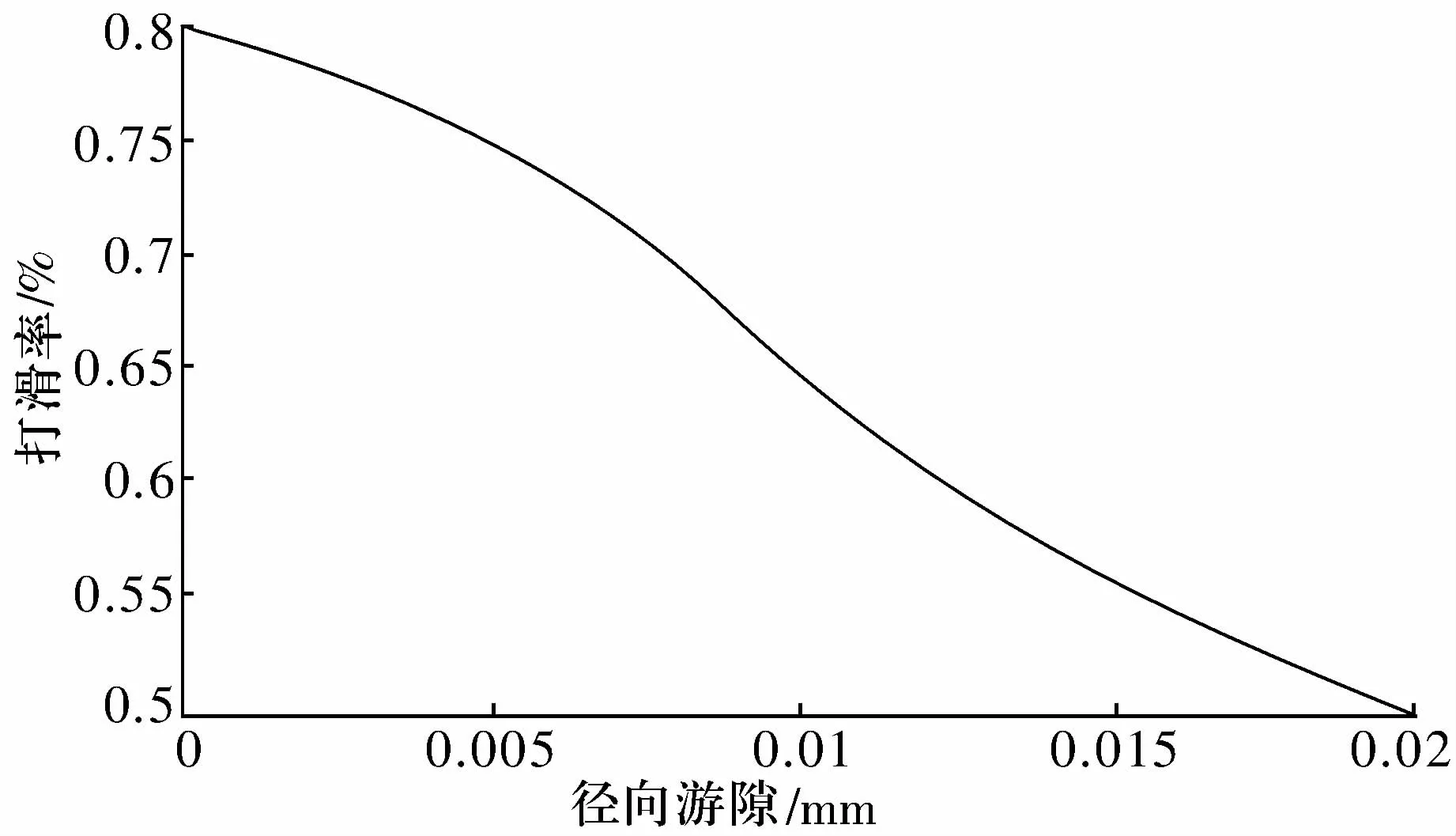
圖6 軸承徑向游隙與保持架打滑率的關系

徑向游隙的增大，軸承的載荷分布范圍減小，載荷區受載滾子與滾道間的法向接觸力和切向拖動力都明顯增大，最終使保持架轉速升高，但過大的徑向游隙會降低軸承工作的穩定性。

3.4 計算結果對比分析

剛柔耦合必然給系統帶來重要影響。圖7為剛體保持架和柔性保持架質心運動軌跡的對比。

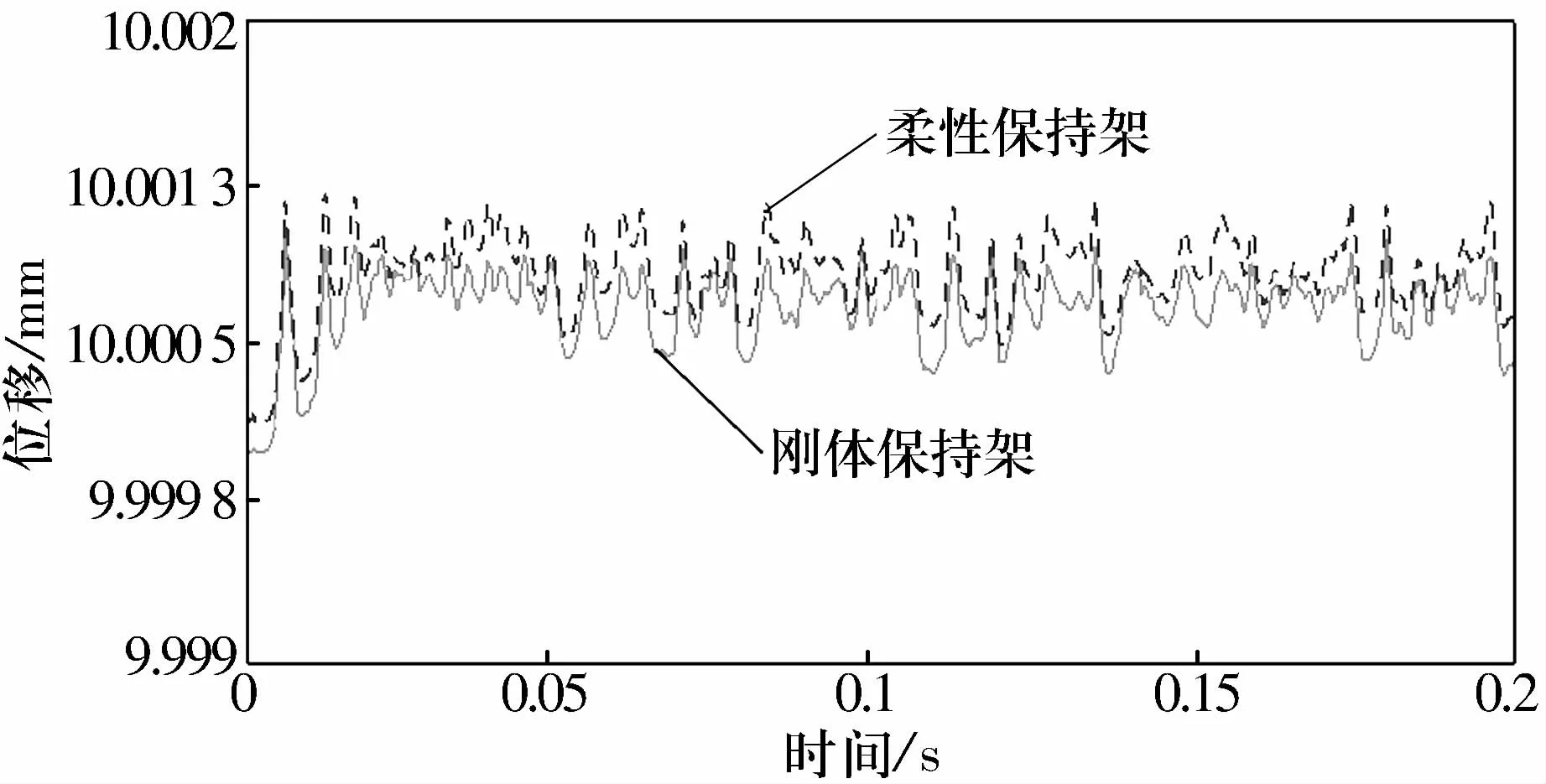
圖7 剛柔保持架質心位移

由圖7可知，柔性保持架的質心位移要稍大于剛體保持架的質心位移，這正是柔性體變形情況的真實體現。圖8為柔性保持架質心運動的軌跡圖，較好地反映了保持架的運動情況。

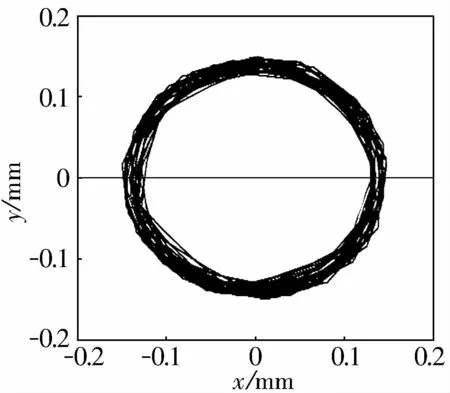
圖8 柔性保持架質心軌跡圖

圖9為耦合模型中保持架與引導套圈之間的流體作用力。軸承設計為外圈引導，該作用力也被稱為保持架與外引導擋邊之間作用力。由于高速下保持架會產生渦動，沿保持架圓周方向的引導間隙會發生變化，所以該作用力會出現圖示的波動，該流體力的大小影響著保持架運動的穩定性，同時也在一定程度上影響著保持架的打滑。

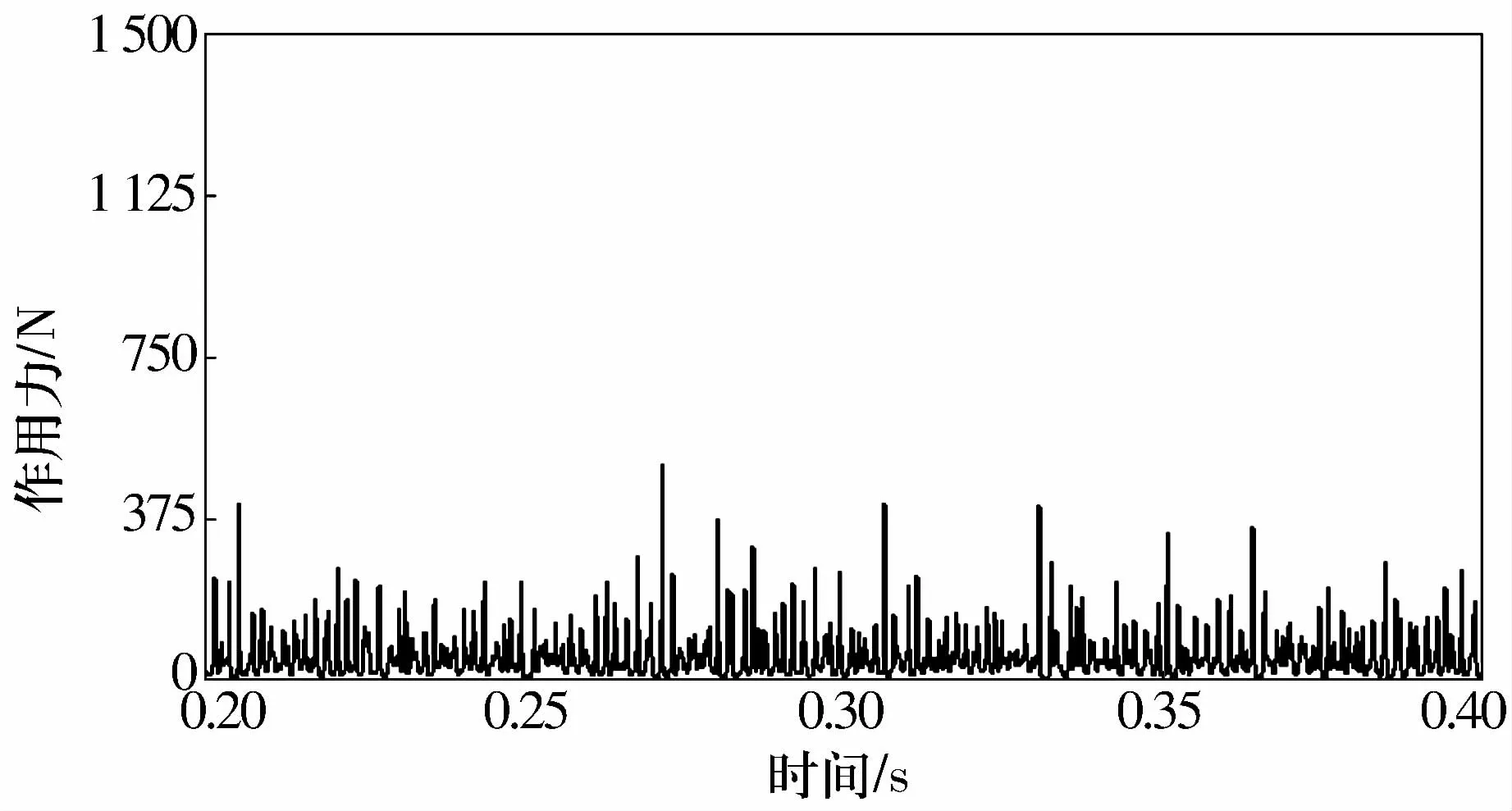
圖9 保持架與引導套圈之間的流體作用力

圖10為耦合模型中滾子與保持架兜孔間的作用力。由圖可以看出，滾子與保持架兜孔間存在著復雜的碰撞情況，而且這種碰撞多發生在滾子進入載荷區和離開載荷區時刻，由于保持架的柔性特性，滾子與保持架間的作用力較少出現大的峰值突變。

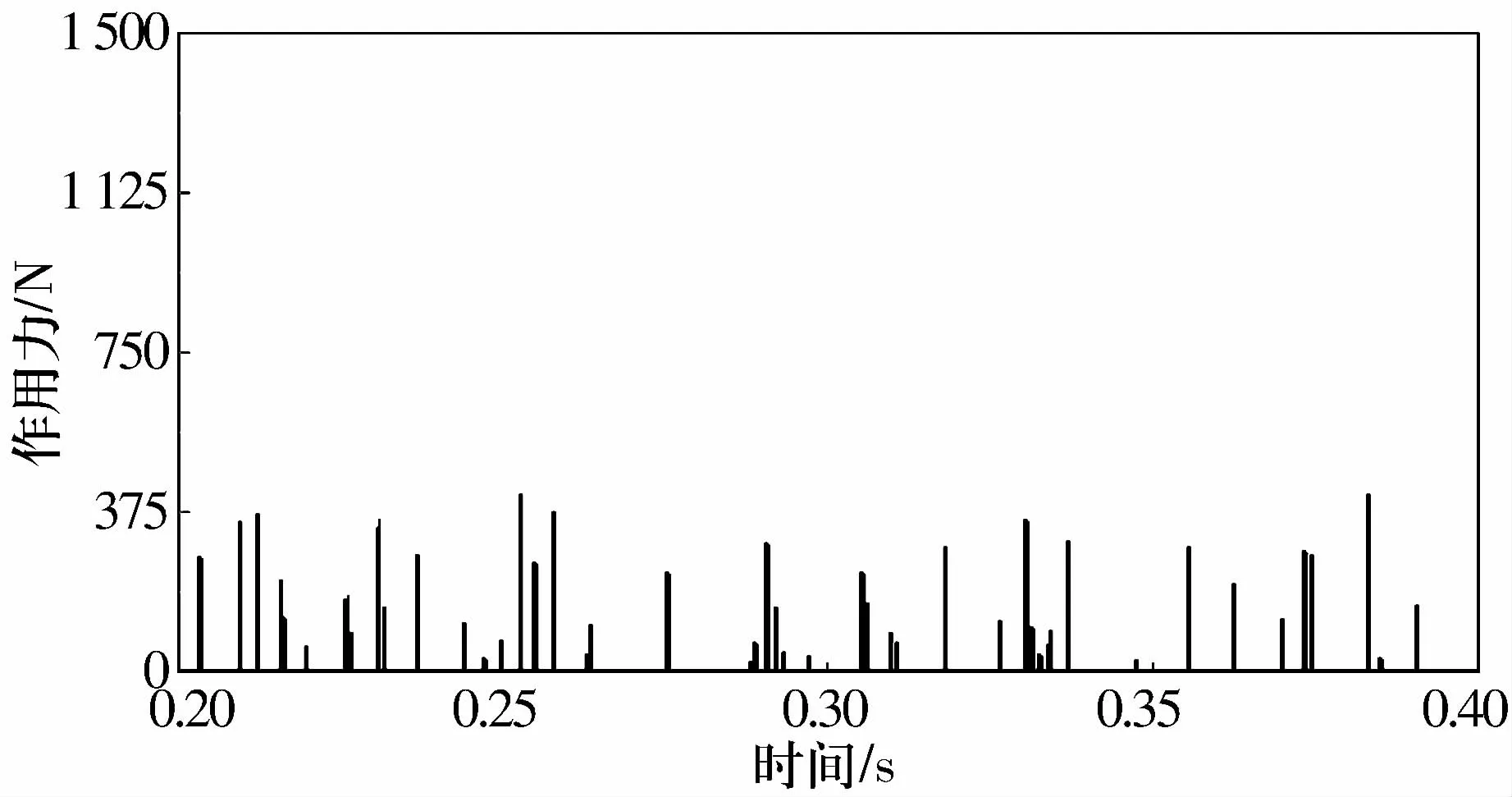
圖10 滾子與保持架兜孔間的作用力

4 結論

（1）由變形引起的應力對保持架過梁影響最大，保持架的破壞一般發生在過梁處。不考慮剛體模態，該保持架沒有小于538.78 Hz的固有頻率。

（2）在考慮軸承壽命因素下，為避免保持架出現較大的打滑率，應該控制軸承最小徑向載荷；過大或過小的徑向游隙都不利于保持架的穩定，實際工作中應按工況要求選擇合適大小的游隙值。

（3）柔性保持架質心位移大于剛體保持架質心位移，但從質心軌跡和保持架兜孔與滾子間作用力來看，柔性保持架具有良好的動態特性，能更好地反映軸承的實際工作狀態。