基于遺傳算法的固定費用運輸問題研究

吳開信，牟瑞芳

（1.西南交通大學(xué) 交通運輸學(xué)院，四川 成都 610031；2.華僑大學(xué) 廈門工學(xué)院，福建 廈門 361021）

運輸問題是線性規(guī)劃的重要分支，很多實際問題可以轉(zhuǎn)化為運輸模型來求解。簡單的線性運輸模型僅考慮兩組約束條件：即與源節(jié)點相關(guān)的m個約束條件和與目的節(jié)點相關(guān)的n個約束條件。固定費用運輸問題(FCTP)是運輸問題的擴展，它除了要考慮兩組約束條件以外，還要考慮每次運輸時的固定成本和與運量有關(guān)的可變成本，簡單的線性運輸問題可以看作所有路徑的固定成本為零的FCTP問題。簡單線性運輸問題的解法通常是用表上作業(yè)法，對于源節(jié)點和目的節(jié)點較多的運輸問題，表上作業(yè)法計算量較大、效率低，而基于遺傳算法運輸問題的求解將更具有實效性。

由于FCTP問題的目標(biāo)函數(shù)具有不連續(xù)性，所以比簡單的線性運輸問題更難處理，Hirsch和Dantzig證明了其最優(yōu)解一般在問題約束條件構(gòu)成的凸集的某個極值點上[1]。在早期的研究中，一些精確解法被運用于求解FCTP問題，如極點排列法和分支定界法等[2]。但這些算法沒有充分利用固定費用運輸問題的網(wǎng)絡(luò)特征，只適合于解決規(guī)模較小的此類問題。后來一些啟發(fā)式算法，如拉格朗日松弛法、模擬退火算法等被引入解決FCTP問題，但在實際運用中發(fā)現(xiàn)這些算法獲得的解質(zhì)量較差。本文根據(jù)FCTP問題的最優(yōu)解是一個生成樹的網(wǎng)絡(luò)特性，結(jié)合遺傳算法設(shè)計出一種基于運輸樹的遺傳算法，并給出實例得出運用此方法可以快速提高獲得最優(yōu)解的幾率。

1 問題的描述

對于FCTP問題，可用以下數(shù)學(xué)模型表示：

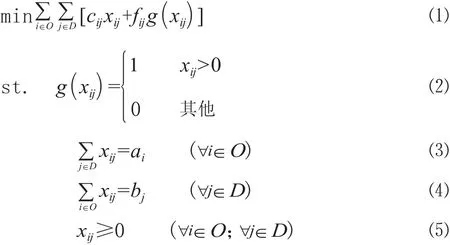
式中：O和D分別表示m個源節(jié)點的集合和n個目的節(jié)點的集合；cij、fij和xij分別表示源節(jié)點i到目的節(jié)點j的單位可變成本、總的固定成本和運輸數(shù)量；條件⑶和條件⑷分別表示產(chǎn)銷平衡條件下物資總的供應(yīng)量和總的需求量，如果是產(chǎn)銷不平衡運輸問題，可以通過增加一個虛擬產(chǎn)地或虛擬銷地轉(zhuǎn)化為產(chǎn)銷平衡的運輸問題；目標(biāo)函數(shù)表示求總運輸成本最小的分配方案[3]。

運輸問題可用一個網(wǎng)絡(luò)二分圖來表示，因此可以嘗試運用基于運輸生成樹的遺傳算法來進行求解。假設(shè)某運輸問題有m個源節(jié)點和n個目的節(jié)點，則FCTP問題的運輸網(wǎng)絡(luò)圖具有以下3個特點：①由于約束方程最多有m+n-1個獨立方程，即系數(shù)矩陣的秩小于等于m+n-1，因此共有m+n-1個基變量，每個變量對應(yīng)運輸表中的1格；②基變量一定能構(gòu)成1棵運輸樹，即在運輸表中的每一行和每一列中至少存在1個基變量；③基變量不能構(gòu)成閉合回路。

2 基于運輸樹的遺傳算法

2.1 編碼

設(shè)集合O表示m個源節(jié)點的集合，O={1,2,…,m}，集合D表示n個目的節(jié)點的集合，D={m+1,m+2,…,m+n}，則運輸網(wǎng)絡(luò)圖中有m+n個節(jié)點和mn條邊。

運輸問題有特殊的數(shù)據(jù)結(jié)構(gòu)，由圖論知識可知，對于1個含m+n個節(jié)點的完備圖，可以表示(m+n)m+n-2棵標(biāo)號不同的樹，也就是說，我們可以用m+n-2個數(shù)字的排列表示m+n個節(jié)點的樹，其中任何樹至少有2片葉子[4]。

在{1,2,…,m+n}共m+n個數(shù)字中隨機可重復(fù)地選取m+n-2個數(shù)字按順序排成1排，構(gòu)成1個初始染色體，染色體中的基因可以相同。運輸樹和染色體之間的轉(zhuǎn)換關(guān)系按下列法則。

2.1.1 運輸樹轉(zhuǎn)換成染色體

步驟1：令i是樹中最小的葉子節(jié)點，j為i的關(guān)聯(lián)節(jié)點，選擇j為染色體中最右邊的數(shù)字，再刪除節(jié)點i和邊(i,j)；

步驟2：重復(fù)上一步m+n-2次，直至剩下2個節(jié)點為止，此時染色體生成。

2.1.2 染色體轉(zhuǎn)換成運輸樹

設(shè)P為一個染色體，S為{1,2,…,m+n}中沒有在P里出現(xiàn)的所有數(shù)字構(gòu)成的集合。設(shè)i是S中最小的數(shù)字，j是P中最左邊的數(shù)字，重復(fù)以下步驟，直至P中沒有數(shù)字為止。

步驟1：若i∈O和j∈D，則(i,j)構(gòu)成運輸樹的1條邊，否則選擇j后面與i不在同一個集合中的元素k，交換 j 和 k 的位置，此時(i,k)構(gòu)成運輸樹的1條邊。

步驟2：從S中去掉元素i，若P中仍含有與j相同的元素，則從P中直接去掉元素j即可；否則從P中直接去掉元素 j 后，在S中增加元素j。

步驟3：若P中沒有元素了，則S中剩下的最后兩個元素構(gòu)成運輸樹的第m+n-1條邊。

步驟4：分配運行量x?=

步驟5：更新產(chǎn)量ai=ai-xij和銷量bj=bj-xij。

步驟6：若沒有可行的運量分配，則停止；否則，去掉運量為0的邊，對產(chǎn)地r和銷地s增加邊(r,s)，且xij=ar=bs。

運輸樹總可以按上面的法則轉(zhuǎn)換為染色體，反之不然，只有可行的染色體才能通過上面的法則轉(zhuǎn)換成運輸樹。由于初始染色體是從{1，2，…，m+n}中隨機可重復(fù)地選取m+n-2個數(shù)字產(chǎn)生，未必是可行染色體，即初始染色體未必能生成1棵運輸樹，在此必須根據(jù)運輸樹特殊的數(shù)據(jù)結(jié)構(gòu)制定可行性準(zhǔn)則，對初始染色體進行篩選。

由運輸樹圖形可知，染色體中出現(xiàn)次數(shù)為t的基因(節(jié)點)與其他節(jié)點有t+1個連接，由此對初始染色體可制定以下可行性準(zhǔn)則：，其中Lo和LD分別表示染色體中含集合O基因的連接數(shù)和含集合D基因的連接數(shù)，分別表示集合S中含集合O基因的個數(shù)和含集合D基因的個數(shù)。

可行性初始染色體可以編制計算機程序在java環(huán)境下執(zhí)行生成。

2.2 適應(yīng)函數(shù)

適應(yīng)度是1個群體中個體生存機會選擇的惟一確定性指標(biāo)，適應(yīng)度較高的個體遺傳到下一代的概率較大。適應(yīng)函數(shù)可表示為：

2.3 選擇策略

采用最優(yōu)方式實現(xiàn)選擇操作，即在父代種群中適應(yīng)度最大的染色體在子代中至少出現(xiàn)1次，然后按照輪盤賭選擇的方式進行選擇操作，以保證優(yōu)良的染色體進入到下一代。

2.4 單點交叉操作

在父代A和父代B中作如下交叉操作：隨機選擇1個交叉點r，把每個染色體分成2個子集，前面子集中的元素及順序不變，后面子集相互交換元素。

2.5 變異操作

可使用位移變異法，即在可行染色體中隨機選擇基因串，插入隨機選定的位置。由于變異操作只是產(chǎn)生基因位置的改變，所以變異后的染色體仍然滿足可行性準(zhǔn)則。

3 實驗及其結(jié)果分析

某公司下設(shè)3個工廠生產(chǎn)某種產(chǎn)品，每日的產(chǎn)量分別是O1=7 t，O2=4 t，O3=9 t，該公司把生產(chǎn)的產(chǎn)品運往4個銷售點，各個銷售點每日的銷量為D4=3 t，D5=6 t，D6=5 t，D7=6 t。已知從各個工廠運往各個銷售點的單位可變成本和固定成本見表1，求總運費最少的運輸方案。

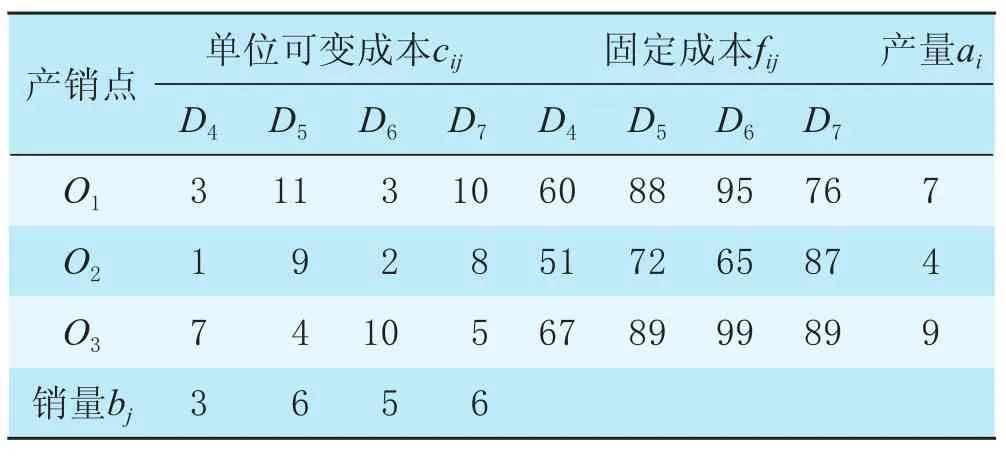
表1 產(chǎn)量、銷量、單位可變成本和固定成本表

求解步驟：

（1）根據(jù)題意建立數(shù)學(xué)模型，確定適應(yīng)函數(shù)。

（2）按可行性規(guī)則，在java程序環(huán)境下在{1,2,…,7}中隨機可重復(fù)地選取5個數(shù)字生成初始可行性染色體，進而組成初始種群，本文可選取種群規(guī)模為30。

如某一個初始染色體為{2,6,3,7,1}時，Lo=6，，即滿足可行性規(guī)則，對應(yīng)的運輸樹見圖1，對應(yīng)的運輸分配量見表2。

圖1 初始染色體{2,6,3,7,1}對應(yīng)的運輸樹

表2 初始染色體{2,6,3,7,1}對應(yīng)的運輸分配量

適應(yīng)度為：(4×3+95)+(3×10+76)+(3×1+51)+(1×2+65)+(6×4+89)+(3×5+89)=551。

（3）選擇操作。父代種群中適應(yīng)度最大的染色體在子代中至少出現(xiàn)1次，然后按照賭盤選擇的方式進行選擇操作。

（4）交叉操作。選用單點位移交叉，交叉概率為Pc=1。

如某一個初始染色體為{1,5,2,6,3}時，Lo=6，，即滿足可行性規(guī)則

對應(yīng)的運輸樹見圖2，對應(yīng)的運輸分配量見表3。

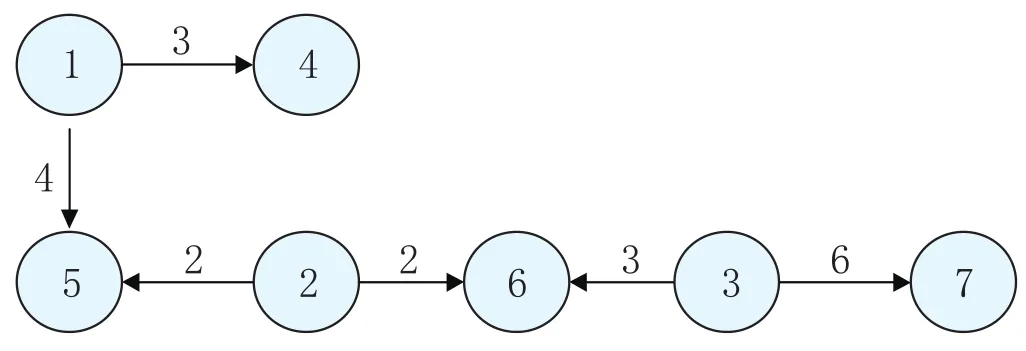
圖2 初始染色體{1,5,2,6,3}對應(yīng)的運輸樹

表3 初始染色體{1,5,2,6,3}對應(yīng)的運輸分配量

符合可行性準(zhǔn)則的父代染色體通過交叉操作總可產(chǎn)生可行的子代，通過解碼得到相應(yīng)的運輸樹。

例如：父代1＜2,6,3,|7,1＞和父代2＜1,5,2,|6,3＞通過交叉操作，得到子代1＜2,6,3,|6,3＞和子代2＜1,5,2,|7,1＞。

對于子代1＜2,6,3,|6,3＞，Lo=5，=1，LD=3，=3，滿足可行性準(zhǔn)則，子代1的解碼圖見圖3。

圖3 子代1的解碼圖

由于x26=0，x36=0，節(jié)點7還需求3個單位，而節(jié)點1還有2個單位沒有分配，節(jié)點2還有1個單位沒有分配，所以增加邊(1,7)和（2,7），x17=2，x27=1。對應(yīng)的運輸樹如圖4表示。

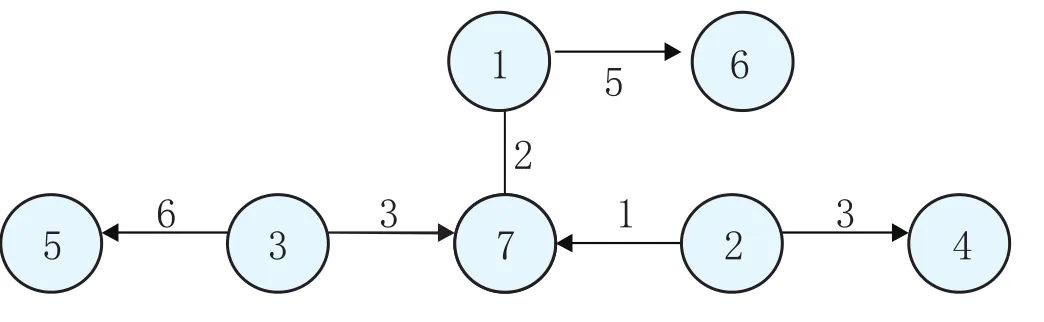
圖4 子代1的運輸樹

對于子代2＜1,5,2,|7,1＞，Lo=5，=1，LD=4，=2，即滿足可行性規(guī)則，子代2對應(yīng)的運輸分配量見表4。

表4 子代2＜1,5,2,|7,1＞對應(yīng)的運輸分配量

同理，由于x17=0，x25=0，節(jié)點7還需求2個單位，節(jié)點6還需求1個單位，而節(jié)點3還有3個單位沒有分配，所以增加邊(3,6)和（3,7），x36=1，x37=2。子代2的運輸樹見圖5。

圖5 子代2的運輸樹

（5）變異操作。使用位移變異規(guī)則，變異概率選取Pm=1/6。最大代數(shù)目取M=100。通過上述遺傳操作過程，可以得出該問題的最優(yōu)染色體為{3,5,2,6,1}，解碼得：x16=6,x17=7,x25=0,x26=4,x34=3,x35=6,目標(biāo)函數(shù)值為508。

4 結(jié)論

遺傳算法是模擬自然選擇和生物進化遺傳過程而提出并發(fā)展起來的搜素算法，此法能以較大概率尋求到問題的最優(yōu)解，因而受到不同領(lǐng)域研究人員的重視[5]。本文針對固定費用運輸問題的特點提出基于運輸樹的遺傳算法，給出了能表示基解的染色體編碼方法，制定了染色體有效性判斷規(guī)則，并通過計算機程序生成有效初始種群，利用選擇、交配、變異規(guī)則最終得出滿意解。最后運用實例對算法的有效性進行了驗證。

[1] Murty KG. Solving the fixed charge problem by ranking the extreme points[J]. Operations Research，1968，16：268-279.

[2] Palekar US, Karwan MK, Zionts S. A branch-and-bound method for the fixed charge transportation problem[J].Management Science，1990，36(9)：1092-1105.

[3] 郭耀煌. 運籌學(xué)[M]. 成都：西南交通大學(xué)出版社，2000.

[4] 玄光男，程潤偉. 遺傳算法與工程優(yōu)化[M]. 北京：清華大學(xué)出版社，2005.

[5] 刑文訓(xùn)，謝金星. 現(xiàn)代優(yōu)化計算方法[M]. 北京：清華大學(xué)出版社，1999.