基于粗糙集和模糊神經網絡的空氣質量評價*

徐彩霞 ，李義杰

(1.遼寧工程技術大學 研究生學院，遼寧 葫蘆島 125105；2.遼寧工程技術大學 軟件學院，遼寧 葫蘆島 125105)

隨著科技和經濟的迅速發展，工業廢氣、機動車尾氣、塵埃等急劇增加，成為空氣質量下降的污染源，對人們的身體健康構成了嚴重威脅，因此采取控制和改善空氣質量的有效措施，合理地進行空氣質量評價及預測成為當前環境科學研究的重要內容之一。

常規的空氣質量評價方法有：API法、灰色聚類法、模糊綜合評價法及模糊灰色模型等。但這些方法都存在著一些不足，如評價結果或多或少受主觀因素的影響。近年來，有人把神經網絡應用到空氣質量評價上并取得了較好的效果。人工神經網絡ANN(Artificial Neural Nets)具有較強的非線性映射、自學習、自適應及容錯能力，它能模擬大腦的思維，利用存儲的網絡信息對未知樣本進行評價。

模糊數學是研究和處理自然界與信息技術中廣泛存在的模糊現象的數學(其中的相對隸屬度能很好地表示模糊概念的相對狀態)，但它很難表示時變知識和過程，而神經網絡能夠通過自學習功能來獲得精確的或模糊的知識，兩者的融合即模糊神經網絡，彌補了模糊數學在學習方面的不足和神經網絡在處理模糊數據方面的缺陷。

粗糙集理論是一種處理不完整和不確定知識的數學工具，它是Z.Pawlak于1982年提出的。粗糙集能有效地分析和處理不精確和不完整等各種不完備信息，并從中發現隱含的規律。

本文把粗糙集理論和模糊概率神經網絡知識運用到空氣質量評價過程中，簡化了網絡模型，提高了評價效率和評價結果的客觀性。

1對粗糙集模糊概率神經網絡的描述

1.1粗糙集屬性約簡問題

知識約簡是粗糙理論的重要內容之一，即求出信息系統的原有屬性集合的一個極小子集，且該子集具有與原屬性集合相同的分類能力，這樣既保證了分類的質量，也提高了分類的速度。

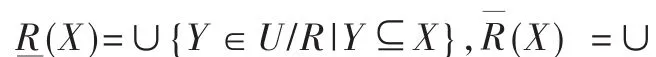
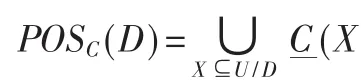
定義3 分辨矩陣由Skowron提出，其定義是：令S=(U，A，V，f)是一個知識表達系統，其中 U={x1，x2，…，xn}是論域；A=C∪D是屬性集合；子集C和D分別是條件屬性集和決策屬性集；V=∪Va，Va∈A，Va表示屬性值的集合；f=U×A→V是一個信息函數，對 xi∈U，a∈A，有f(xi，a)∈Va；D(x)是樣本 x在 D 上的值，則分辨矩陣記為M=[mij]n×n，第 i行第 j列的元素為 mij[1]：

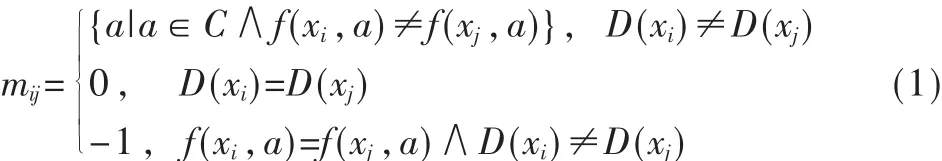
其中n=|U|。

1.2指標相對隸屬度矩陣

若空氣質量有b個級別，c項評價指標，則這c項指標對應的b級評價標準構成了空氣質量評價的標準值矩陣：

式中yij為第i項評價指標的第j級的評價標準值(1≤i≤c，1≤j≤d)。

令m為空氣質量檢測樣本的個數，這m個檢測樣本數據構成了樣本值矩陣X：

式中：xik為第k個檢測樣本數據的第i項評價指標值，(1≤i≤c，1≤k≤m)。

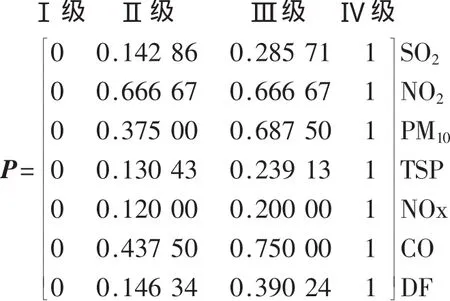
空氣污染程度的大小是個模糊概念，因此采用模糊數學理論中的相對隸屬度來描述。令pij為第i項指標的第 j級標準值的相對隸屬度(1≤i≤c，1≤j≤d)，pij值的大小代表了空氣污染的程度。再令rik為第k個檢測樣本數據的第i項指標的等級相對隸屬度(1≤i≤c，1≤k≤m)。則標準指標相對隸屬度矩陣P=[pij]c×d和檢測樣本指標相對隸屬度矩陣 R=[rik]c×m分別為[2]：

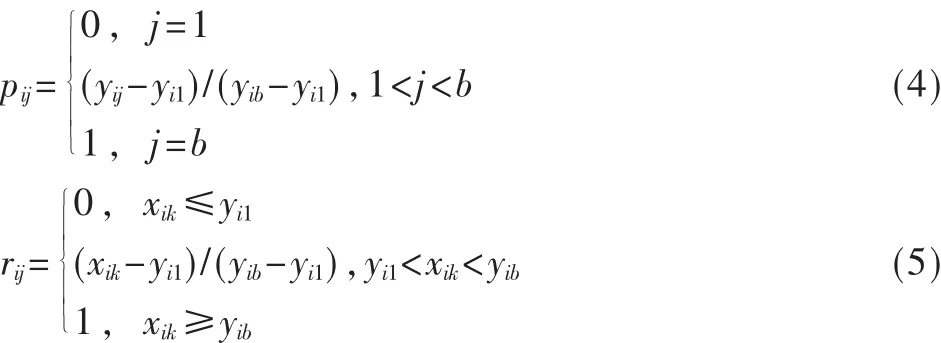
1.3 基于粗糙集模糊概率神經網絡的空氣質量評價模型的框架結構

與常用的BP神經網絡相比，概率神經網絡(PNN)是一種結構簡單、訓練速度快、非線性映射能力強且具有較好分類能力的神經網絡模式。但若PNN有多個輸入或大量的訓練樣本數據，分類結果的準確性就可能降低，同時也降低了網絡的訓練速度。因此需要運用粗糙集理論中的知識約簡算法對屬性進行約簡，也就是在保證知識表達系統在分類能力不變的條件下，刪除不重要或不相關的條件屬性，減少PNN的輸入神經元的個數，從而提高訓練速度。

為了使整個評價模型的指標具有可比性，采用了模糊數學理論中的相對隸屬度的知識，對約簡后的評價標準數據進行預處理，并構造相對隸屬度矩陣，這樣就能較清晰地反映空氣質量評價中的各指標的相對狀態，并在此基礎上構建模糊概率神經網絡(FPNN)模型。

根據粗糙集和FPNN模型對問題分析的思路，空氣質量評價模型的框架結構可以用圖1所示的流程圖描述。

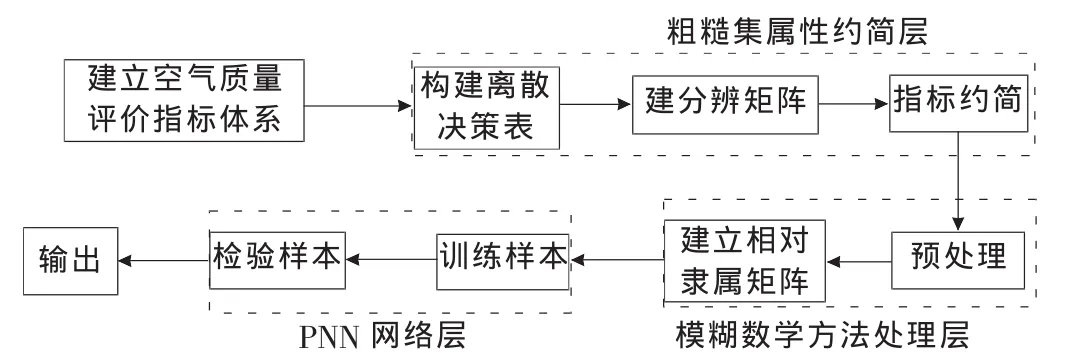
圖1 基于粗糙集的FPNN空氣質量評價模型的框架結構

2基于粗糙集FPNN空氣質量評價模型的實例

2.1指標體系的建立

指標體系的選擇直接影響到評價結果的準確性，若評價指標太多，就會延長神經網絡訓練的時間，若指標太少，就可能降低評價結果的準確性。根據中華人民共和國國家標準(GB3095-1996《環境空氣質量標準》及2000年的[2000]1號文件)及我國空氣污染的特點可知，影響我國空氣質量的評價指標有：SO2、NOx、TSP(懸浮顆粒物)、PM10、DF(降塵)、NO2、CO。

2.2粗糙集屬性約簡

2.2.1屬性約簡的步驟

粗糙集理論只能處理離散的數據，因此需要進行連續屬性的值離散化，它可以由領域專家根據經驗給出相應的區間，也可以根據某種原則對空間進行劃分，給出離散點進行離散化。本文采用后者。區分矩陣法是計算決策表屬性約簡的常用方法，但它沒有充分考慮到數據的不相容度，只適用于相容決策表。下面給出最佳屬性約簡算法的步驟：

(1)連續數據的離散化；

(2)構 造 分 辨 矩 陣 M=[mij]n×n；

(3)確定 D的C正域POSC(D)，可按照文獻[3]所提出的簡便方法來快速確定POSC(D)；

(4)判斷C中各屬性 ci是否對D可約簡，方法是當去掉屬性 ci時，檢驗正域 POSC(D)≠POSC-{ci}(D)是否成立。若成立，則 ci不可約簡，否則，ci可約簡[4]；

(5)按步驟(3)～(4)遍歷所有屬性；

(6)所有不可約簡的屬性集合為約簡后的指標，即條件屬性C對于決策屬性D的一個相對約簡。

2.2.2空氣質量評價指標的約簡

為了更清楚地了解空氣的質量狀況，在三級基礎上增加一級，即將空氣質量劃分為四個等級，分別為：Ⅰ級、Ⅱ級、Ⅲ級和Ⅳ級。選取10個城市的數據，這10個城市污染差別顯著，可以作為屬性約簡的樣本(篇幅有限，此數據不再列出)。 令 a1、a2、a3、a4、a5、a6、a7分別表示條 件 屬 性(空 氣 質 量 評 價 指 標)中 的 ：SO2、NOx、NO2、PM10(可吸入顆粒物)、TSP(總懸浮顆粒物)、CO、DF(降塵)。 然后對屬性值進行離散處理：令xik為第i個樣本第k項指標值，yjk為第 k項指標的第 j級標準值，pk為所取樣本的第 k項指標離散處理后的值。當 xik≤y1k時，pk=0；當y1k＜xik≤y2k時，pk=1；當 y2k＜xik≤y3k時，pk=2；當 y3k＜xik≤y4k時，pk=3；當 xik≥y4k時，pk=4。 其中我國空氣質量分級標準如表1所示。決策屬性D的屬性值與空氣質量等級的對 應 關系 是 ：1——Ⅰ級 ，2——Ⅱ級，3——Ⅲ級 ，4——Ⅳ級，這樣可得到離散化后得到的決策表如表2所示。然后根據公式(1)建立分辨矩陣(篇幅有限，不再顯示)，應用屬性約簡的步驟(3)～(6)，最后得到約簡后的指標是：SO2、NO2、TSP、PM10。

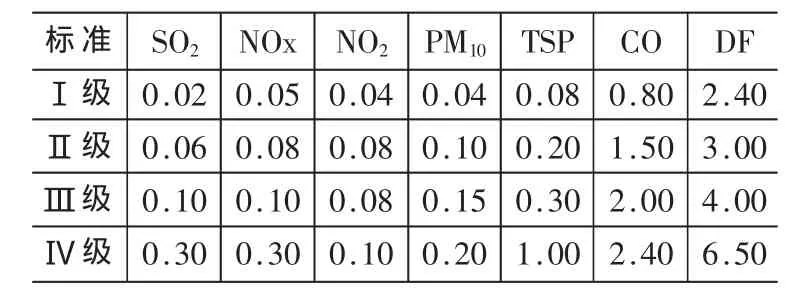
表1 空氣質量分級標準[5]

2.3相對隸屬度矩陣的建立及FPNN的仿真研究

在保證相同分類結果的情況下，粗糙集理論的屬性約簡去掉了不相關或不重要的屬性，約簡后的指標為：SO2、NO2、PM10和 TSP，這 4 個指標的值越小，表示空氣受污染的程度越小，其分級標準見表1，再按2.2節所述方法，構造出標準隸屬度矩陣P(篇幅有限，檢測樣本指標相對隸屬度矩陣R略)。

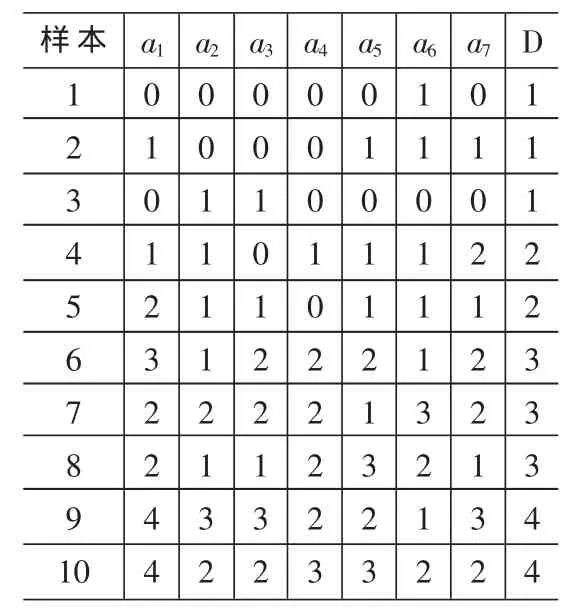
表2 離散化后的決策表

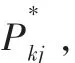
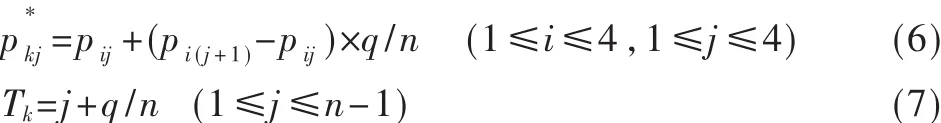
根據需要，取 n=5，共生成 16個樣本，將樣本 1、2、4、6、7、9、10、11、13、15、16 作為訓練樣本， 其余 5 個作為檢驗樣本。SO2、NO2、PM10和 TSP作為輸入向量，本實驗是基于Matlab7.0軟件來實現整個模糊概率神經網絡空氣質量評價過程的，則輸入層有4個神經元，徑向基層的神經元個數同訓練樣本的個數相同，即為11個，將評價等級作為目標向量輸出。本文空氣質量評價共分4級，分別對應的等級值為 1、2、3、4，則有 4個競爭神經元；經過參數尋優運算，確定高斯函數的平滑參數為0.03～0.15之間時效果最為理想。訓練結果如表3所示，可見對于訓練樣本和檢驗樣本，網絡的判斷率都達到了100%。但指標約簡后的神經網絡模型結構簡單，樣本訓練所用的時間更少。

由于影響空氣質量的因素很多，導致了指標體系存在冗余，因此有必要進行指標約簡。約簡后的指標有：SO2、NO2、PM10和 TSP，這說明目前我國空氣質量主要受這四種污染物的影響，為我國有關部門合理地制定空氣污染防治措施提供了依據。模糊數學理論中的相對隸屬度能夠表明空氣質量指標的相對狀態，克服了采用最大隸屬度時存在的只考慮極值、容易丟失中間信息的缺陷，將它和概率神經網絡相結合，建立了模糊概率神經網絡模型(FPNN)，該模型人為調節參數，使評價結果更客觀合理，并且為了提高評價結果的質量，采用了在標準相對隸屬度矩陣中進行插值的方法，生成更多的樣本。仿真表明，指標約簡后FPNN模型既保證了分類質量，也提高了收斂速度，實用性更強。當然本文所采用的空氣質量評價方法也可以應用到其他領域中。

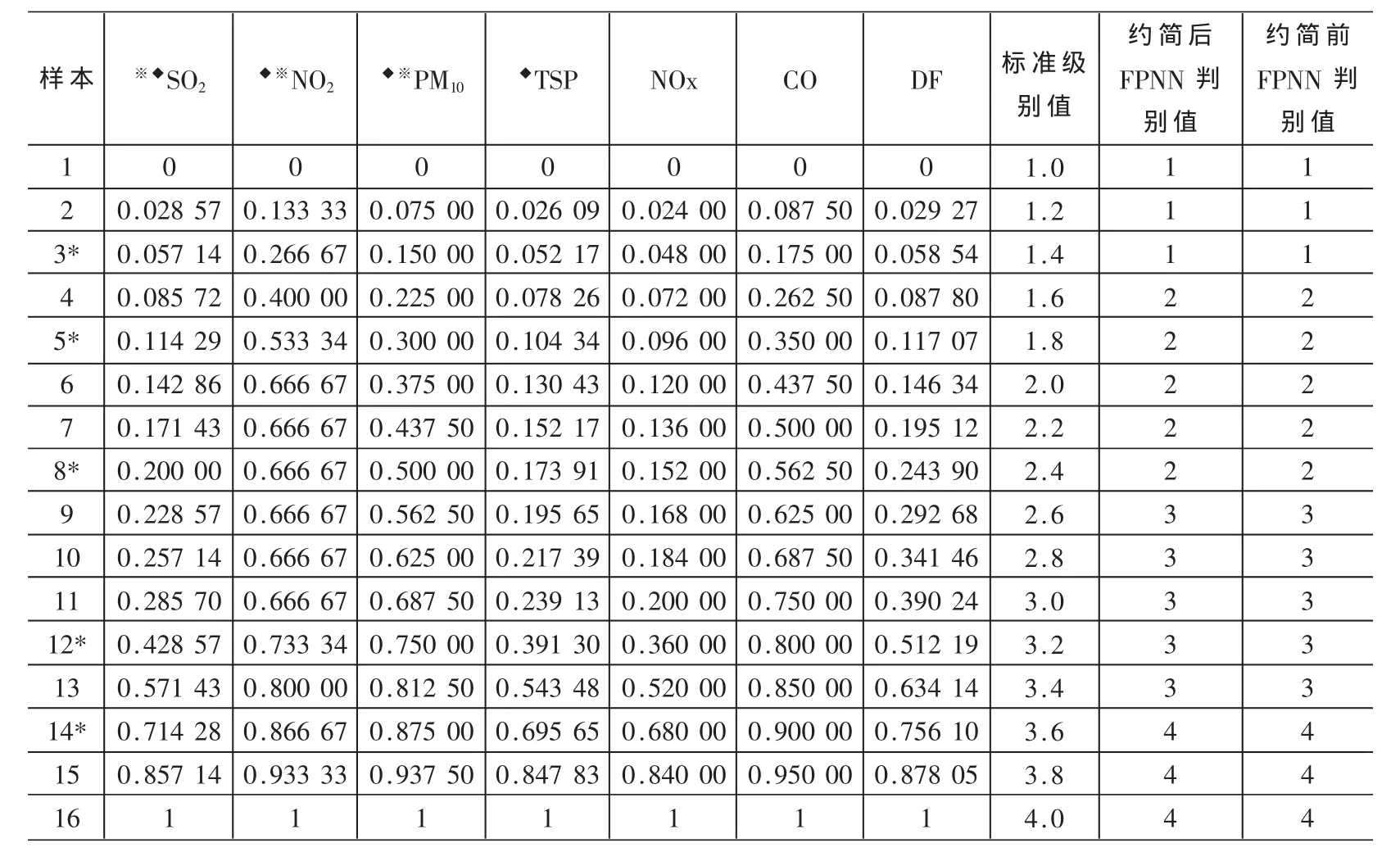
表3 基于相對隸屬度矩陣的FPNN訓練和樣本檢驗及其結果

[1]史成東，陳菊紅，胡健.基于粗糙集和神經網絡的供應鏈績效預測研究 [J].計算機工程與應用，2007，43(33)：203-206.

[2]劉坤，劉賢趙.模糊概率神經網絡模型在水質評價中的應 用[J].水 文,2007，27(1)：36-39.

[3]汪小燕.基于分辨矩陣的論域劃分方法[J].電腦學習，2007(4)：5-6.

[4]李錦菊，沈亦欽.中美兩國環境空氣質量標準比較[J].環境監測管理與技術，2003，15(6)：24-26.

[5]飛思科技產品研發中心.神經網絡理論與MATLAB 7[M].北 京 ：電 子 工 業 出 版 社,2005：116-127.