UC安全的基于一次簽名的廣播認證

張俊偉，馬建峰，楊力

（西安電子科技大學 計算機網絡與信息安全教育部重點實驗室，陜西 西安 710071）

1 引言

并發組合是現實網絡環境中的實際情形，在孤立模型中證明安全的協議在組合情形下不一定是安全的。因此，在孤立模型中證明協議的安全性還是不夠的。UC（universally composable）安全的概念源于由Canetti在2001年提出的基于計算復雜性的UC框架[1]。UC框架主要用于描述和分析并發環境下的協議安全問題。UC框架中最重要的屬性是它能夠確保協議的UC安全，即在UC框架下證明安全的協議，在與其他協議并發運行的情況下，或者該協議作為一個系統的組件時，仍能保證協議的安全性。理想函數是UC框架中非常重要的安全概念，它扮演著一個不可攻陷的可信第三方的角色，能夠完成協議所需的特定功能。UC框架中已經定義了多個最基本的理想函數，如認證消息傳輸、安全消息傳輸、密鑰交換、公鑰加密及簽名、承諾、不經意傳輸[2]等。

Lamport首次提出了一次簽名的概念[3]，即使用一對公/私鑰對只能對一條消息進行簽名。BiBa[4]是第一個高效地適用于低能量設備的一次簽名方案。Mitzenmacher和Perrig改進了BiBa并提出了Powerball[5]。然而，BiBa和Powerball僅能在隨機預言（RO, random oracle）模型下證明是安全的。Reyzin L和Reyzin N提出了另一個高效的一次簽名方案 HORS[6]。HORS的安全性是基于單向函數（one-way functions）和subset-resilient散列函數的。由于 subset-resilient散列函數是一個較強的安全假設，針對HORS出現了一些改進方案：Pieprzyk等設計了一個基于單向函數和cover-free families可證明安全的一次簽名方案[7]，但其通信開銷和密鑰長度都比HORS要大很多，不適合低能量設備。Park和Cho提出了2個一次簽名方案[8]：方案1的安全性基于無碰撞散列函數（collision-resistant hash functions）和單向函數，但該方案簽名生成的開銷較大；而方案2僅是在RO模型下安全的。

基于一次簽名的廣播認證作為廣播認證的一種解決方案具有以下優點[9]：1）計算效率高，一次簽名的計算效率比傳統的數字簽名高，適用于低能量設備；2）即時認證，不存在認證時延，適用于對認證時間敏感的環境；3）不需要時間同步；4）不可否認性。

本文在UC框架下研究了基于一次簽名的廣播認證的問題。具體貢獻如下。1）設計了一次簽名的理想函數FOTS，FOTS滿足一次簽名的安全需求且具有適應性選擇消息的不可偽造性（EU-COMA,existential unforgeable against chosen one message attack）。2）改進 HORS，提出了一次簽名協議HORS+。基于單向函數和無碰撞散列函數，HORS+能夠安全實現理想函數 FOTS。3）構造了廣播認證理想函數FBAUTH，在(FOTS，FREG)-混合模型下設計了能夠安全實現FBAUTH的協議πBAUTH。4）根據組合定理，組合HORS+，在πBAUTH的基礎上構造UC安全的廣播認證協議。

文章剩余部分安排如下：第2節簡要介紹UC框架的相關概念；第3節設計了一次簽名理想函數FOTS和協議HORS+；第 4節提出了廣播認證理想函數FBAUTH和協議πBAUTH；第5節是結束語。

2 UC框架

UC框架如圖1所示。首先，UC框架定義了現實環境。現實環境描述協議的真實運行情況，其中所有參與方在真實敵手攻擊A存在的環境下運行真實協議。其次，UC框架定義了理想環境用來描述密碼協議的理想運行。在理想環境下，存在虛擬參與方，理想敵手S和理想函數F。參與方之間以及敵手S與參與方不直接通信；所有參與方和敵手S均與理想函數交互。理想函數本質上是一個不可攻陷的可信角色，用來完成協議所需的理想運行和功能。在UC的安全框架中，環境Z來模擬協議運行的整個外部環境（包括其他并行的協議、攻擊者等），Z可以與所有的參與者以及攻擊者A和S直接通信，Z不允許直接訪問理想函數F。

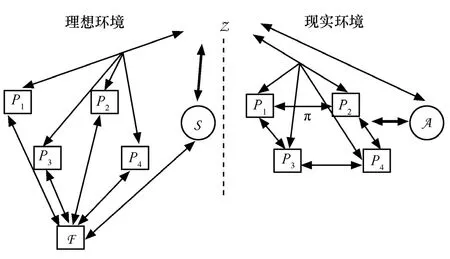
圖1 UC框架

UC仿真[1]。協議 π能夠 UC仿真理想函數 F當且僅當對于任意真實敵手 A，存在理想敵手 S，使得任意環境Z，至多以一個可忽略的概率來區分：存在A及協議π的現實環境和存在S及理想函數F的理想環境。如果協議π能夠UC仿真理想函數F，稱協議π在UC框架下安全實現了理想函數F，也稱協議π是UC安全的。

組合定理[1]。如果協議ρ安全實現理想函數F，且 π 是 F-混合模型[1]下的協議，那么協議 πρ/F（用協議ρ替換協議π中的理想函數F所得到的組合協議）UC仿真 F-混合模型下的協議π。特別地，如果協議π在F-混合模型下安全實現理想函數G，那么協議πρ/F也安全實現理想函數G。

通常復雜的協議由多個子協議構成，每個子協議都可以實現某個安全任務。根據組合定理，利用UC安全的協議可以安全構建一個更為復雜的協議，從而實現指定的任務，并保證相應的安全屬性。

3 一次簽名

3.1 理想函數FOTS

一次簽名的理想函數FOTS如下。

Key Generation

當從S收到(KeyGen, sid)后，其中sid = (S, sid’)。

1) 將(KeyGen, sid)發送給敵手。

當從敵手收到(VerificationKey, sid, v’)。

2) 如 果 存 在 記 錄 (m’, σ’, v’, 1), 發 送KEY_INVALID給敵手。

3) 否則, 令 v =v’, t=0, 并輸出(VerificationKey,sid, v)給 S。

Signature Generation

當從 S收到(Sign, sid, m), 其中 sid=(S, sid’)。

1) 如果 t=1或者 v =⊥, 則發送響應KEY_INVALID。

2) 否則, 發送(Sign, sid, m)給敵手并令t=1。

當從敵手收到(Signature, sid, m, σ), 驗證記錄(m, σ, v, 0)是否存在:

1) 如果存在, 則令t=0, 輸出一個錯誤信息給S；

2) 否則, 輸出(Signature, sid, m, σ)給 S, 并記錄(m, σ, v, 1)。

Signature Verification

當從 V 收到(Verify, sid, m, σ, v’), 發送(Verify,sid, m, σ, v’)給敵手。

當從敵手收到(Verified, sid, m, φ):

1) 如果 v’=v且存在記錄(m, σ, v, 1), 令 f=1；

2) 否則, 如果 v’=v, 簽名者未被攻陷, 且不存在記錄(m, σ’, v, 1), 令 f=0 并記錄(m, σ, v, 0)；

3) 否則, 如果存在記錄(m, σ, v’, f’), 令 f = f’；

4) 否則, 令 f=φ 并記錄(m, σ, v’, φ)；

5) 輸出(Verified, sid, m, f)給 P。

與傳統的數字簽名不同，一次簽名使用一個公/私鑰對只能對一條消息簽名。因此，當FOTS收到來自簽名者的請求時，FOTS首先驗證公鑰的正確性。其中，v記錄當前的公鑰，t表示當前公鑰是否被使用。如果不存在公鑰或者現有的公鑰已經被使用，FOTS不會產生消息的簽名。

EU-COMA: 一次簽名方案Σ = (gen, sig, ver)，其中gen為密鑰生成算法；sig為簽名生產算法；ver為簽名驗證算法。一次簽名Σ滿足EU-COMA當且僅當對于任意概率多項式時間(PPT, probabilistic polynomial time)的敵手F，在獲得一個正確簽名(m,σ)后，成功偽造簽名(m’, σ’)的概率是可忽略的，即Prob[(m’, σ’)←F(m, σ): ver(m, σ, v)=1; m’≠m; ver(m’,σ’, v)=1] ＜ v(k)。

定理1 一次簽名Σ安全實現理想函數FOTS當且僅當一次簽名Σ滿足EU-COMA。

定理1的證明過程與文獻[10]中定理2的證明過程類似，唯一不同的是敵手在一次簽名中只能詢問一條消息的簽名。因此，這里不再贅述。

3.2 一次簽名HORS+

HORS的安全性基于強的假設，即散列函數為subset-resilient散列函數[6]。但是，用現有的復雜性理論假設來實現 subset-resilient散列函數仍然是一個公開問題。為了不依賴subset-resilient散列函數，利用單向函數和無碰撞散列函數來構造協議HORS+。單向函數和無碰撞散列函數的定義請參考文獻[11]。與HORS不同，在HORS+的密鑰生成階段，簽名者計算(x, y=g(x))，將x作為私鑰，y作為公鑰；在簽名生成階段，簽名者將消息與x串聯計算散列值，并將x作為簽名中的一部分；在簽名驗證階段，驗證者首先驗證x是否為y的原像，然后再計算消息和x的散列值。協議HORS+如下：

安全參數 l, L, k, t

無碰撞散列函數 H: X→Y, L=|Y|=k lb t

單向函數 f, g: X→Y, |X|=|Y|=l

Key Generation

當簽名者 S收到(KeyGen, sid), 其中 sid=(S,sid’)。

1) 產生隨機數x和t個隨機的l-比特串s0, s1,…,st-1, 令 y=g(x)和 vi=f(si) (0≤i≤t-1)。

2) 令 v=(y, v0, v1, … , vt-1), s=(x, s0, s1,…, st-1).將s作為私鑰, v作為公鑰, 并輸出(VerificationKey,sid, v)。

Signature Generation

當簽名者 S收到(Sign, sid, m), 其中 sid=(S,sid’)。

1) 計算 h=H(m||x)。

2) 令 h=h1|| h2|| … || hk, ij=hj, 其中|hj|=lb t, 1≤j≤k。

3) σ=(x,si1,si2,…,sik), 輸出(Signature, sid, m, σ)。Signature Verification

當驗證者 V收到(Verify, sid, m, σ, v), 其中sid=(S, sid’), 令 σ = (x,s1′,s2′, … ,sk′), v = (y, v0,v1, … , vt-1)。如果 y≠g(x)，輸出(Verified, sid, m, 0),否則:

1) 計算 h = H(m||x)；

2) 令h=h1|| h2|| … || hk, ij= hj, 其中|hj|=lb t, 1≤j≤k；

3) 如果對于每一個j (1≤j≤k), f(sj′)=vij, 令f=1; 否則, 令 f =0；

4) 輸出(Verified, sid, m, f)。

3.3 協議HORS+實現FOTS

定理2 如果f和g是單向函數，H是無碰撞散列函數，那么HORS+滿足EU-COMA。

證明 令Setk(x)={x1, x2, … , xk| (x1, x2, … ,xk)=x, |x1|=|x2|=…=|xk|=|x|/k}。 在 HORS+中 ，Setk(σ’) ? Setk(σ)與 Setk(h’) ? Setk(h)等 價 。 令FORGER是偽造簽名的攻擊者。給定一個合法簽名(m, σ)，當敵手 FORGER 成功偽造簽名(m’, σ’)時，有以下3種可能的情況。

1) σ’≠ σ 且 Setk(σ’) ? Setk(σ)。 假 定 敵 手FORGER 可以偽造簽名(m’, σ’)且滿足 σ’≠ σ，Setk(h’)?Setk(h)。可以構造敵手 Af求出單向函數 f的逆。假設FORGER能以不可忽略的概率ε1偽造簽名。令εf是敵手Af輸出z且f(z) = y的概率。可以得到

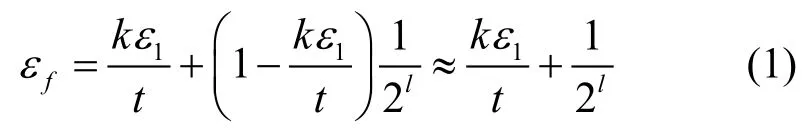
因此εf也是不可忽略的（通常l至少為80，而2-80是可忽略的），這與單向函數的定義相矛盾，因此，敵手 FORGER成功偽造簽名(m’, σ’)的概率是可忽略的。

2) σ’= σ。如果敵手 FORGER可以成功偽造簽名(m’, σ)，可以構造敵手AH輸出散列函數H的碰撞對。如果敵手FORGER 能以不可忽略的概率ε2成功偽造簽名，那么AH輸出碰撞對的概率εH為

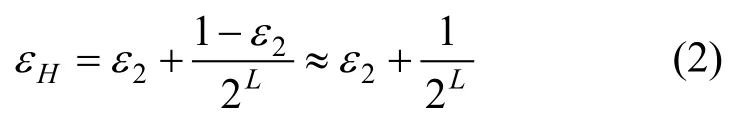
通常情況下的散列函數，L至少是128，概率2-128是可忽略的，因此εH是不可忽略的。這與無碰撞散列函數的概念相矛盾。由此得出結論，FORGER只能以可忽略的概率偽造簽名。

3) σ’≠ σ 且 Setk(σ’)? Setk(σ)。在這種情況下，給定(m, σ)，敵手 FORGER 可以找到 m’滿足Setk(h’)? Setk(h)，其中 h = H(m||x)，h’ = H(m’||x’)，y=g(x’)。如果 FORGER找到這樣的 m’，可以構造Ag求出單向函數g的原像。如果敵手FORGER成功偽造簽名的概率為ε3，則敵手Ag找到單向函數g的原像的概率εg為

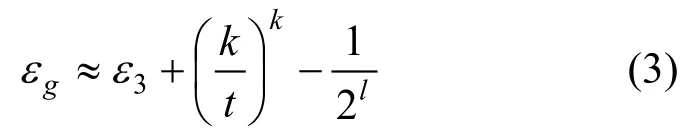
需要說明的是(k/t)k可忽略。例如，通常情況下，當|H(x)|=160，k=16，t=1 024，概率為可忽略的2-96。如果ε3是不可忽略的，那么εg也是不可忽略的，這與單向散列函數的定義相矛盾。由此可知，敵手FORGER偽造簽名的概率是可忽略的。

綜上所述，敵手FORGER偽造簽名的概率為

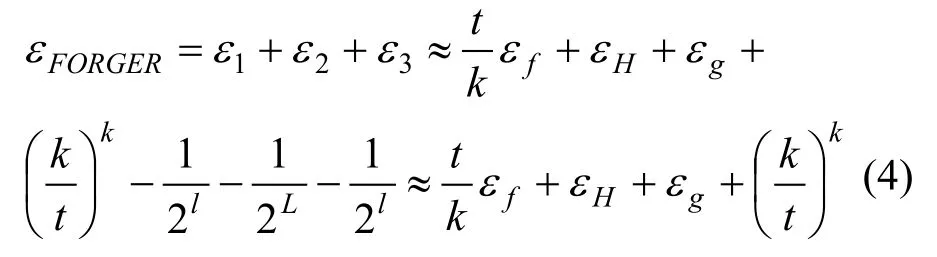
如果f和g為單向函數，H為無碰撞散列函數，那么 εf、εH和 εg都是可忽略的，進而 εFORGER也是可忽略的，即敵手偽造簽名的概率是可忽略的。由于篇幅限制，這里的證明省略了 Af、AH和 Ag的詳細描述。

因此，HORS+滿足EU-COMA。 □

由定理1和定理2，進一步得到定理3。

定理3 如果f和g是單向函數，H為無碰撞散列函數，協議HORS+安全實現理想函數FOTS。

3.4 相關工作比較

表 1將 HORS+與 BiBa、Powerball、HORS以及文獻[8]中的2個協議作比較。基于單向函數和無碰撞散列函數，HORS+是可證安全的，HORS+的安全性不依賴于 RO模型。與 HORS相比，HORS+的安全性基于更弱的假設。同時，比較了RO模型下各個方案的安全性，即敵手在RO模型下偽造簽名的概率（見表1）。與HORS相比，HORS+在密鑰生成和簽名驗證中增加了一次單向函數的計算，而簽名長度和密鑰長度增加一個 l bit的 x。

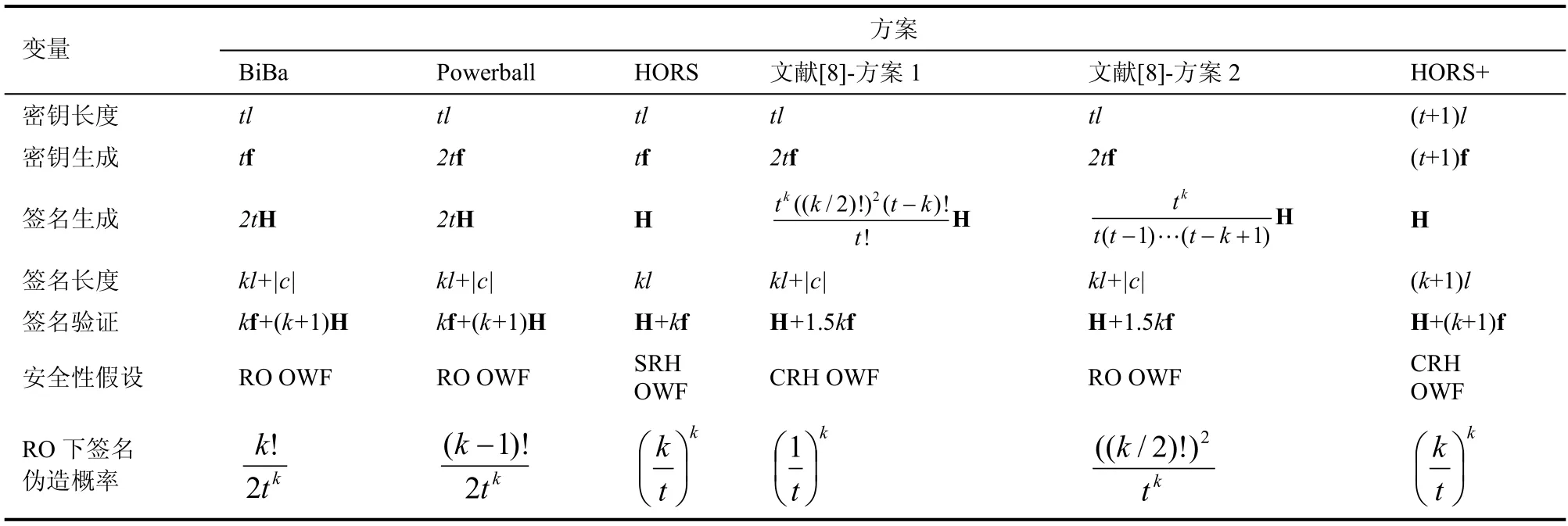
表1 一次簽名協議比較

4 UC安全的廣播認證協議

4.1 理想函數FBAUTH

廣播認證的理想函數保證廣播網內的合法用戶從未被攻陷的廣播者B收到消息m當且僅當B發送了這個廣播消息。廣播認證的理想函數FBAUTH如下。

當從未被攻陷的B收到(Broadcast, sid, m), 其中 sid=(B, sid’): 發送(Broadcasted, sid, m)給敵手。

當從敵手收到(Broadcast, sid, m’):

1) 如果 B未被攻陷, 給廣播網中的所有接受者發送(Broadcasted, sid, m)；

2) 如果B被攻陷且m尚未發送, 給廣播網中的所有接受者發送(Broadcasted, sid, m’)。

非機密性：FBAUTH將廣播認證消息的內容發送給敵手。因此，FBAUTH不保證消息的機密性。

認證性：如果B（未被攻陷）廣播消息m，廣播網中的接收者會收到消息m。如果發送者被攻陷且消息尚未發送，敵手可以篡改廣播消息。

4.2 廣播認證協議πBAUTH

在(FOTS, FREG)-混合模型下，構造了廣播認證協議πBAUTH。πBAUTH利用FREG注冊簽名者的公鑰，驗證者從FREG獲得已注冊的公鑰（FREG的詳細描述見文獻[1]）。πBAUTH操作如下。

當收到(Broadcast, sid, m)時, 其中 sid=(B,sid’)。

1) B發送(KeyGen, sid)給FOTS，當從FOTS收到(VerificationKey, sid, v0), 令 v = v0。

2) B發送(Sign, sid, m)給FOTS, 之后從FOTS收到(Signature, sid, m, σ)。

3) B發送(Broadcast, sid, m, σ), 同時, B發送(Register, sid, v)給 FREG。

當收到(Broadcasted, sid, m, σ), 其中 sid=(B,sid’)。

1) 如果v=⊥, R發送(Retrieve, sid)給FREG, 并獲得(Retrieve, sid, v’)。如果 v’=⊥或者存在一條記錄(m’, v’), R 忽略這條消息; 否則, 令 v=v’。

2) R 發送(Verify, sid, m, σ, v)給 FOTS，隨后從FOTS收到(Verified, sid, m, f)。

3) 如果f =1, R記錄(m, v)并令v =⊥, 隨后R輸出(Broadcasted, sid, m)，否則R忽略這條消息。

4.3 協議πBAUTH實現FBAUTH

定理4 協議πBAUTH在(FOTS, FREG)-混合模型下安全實現理想函數FBAUTH。

證明 令A為現實敵手。構造理想敵手S使得對于任意環境 Z只能以可忽略的概率區分：協議πBAUTH及A交互的現實環境和理想函數FBAUTH及S交互的理想環境。

1) 構造S。

Simulating the sender

當未被攻陷的B收到(Broadcast, sid, m)后, S從FBAUTH獲得這個值并為A仿真協議πBAUTH。

當從FOTS獲得(KeyGen, sid), S發送(KeyGen, sid)給A, 然后將A的響應(VerificationKey, sid, v)轉發給FOTS。

2) 當從 FOTS收到(Sign, sid, m)后, 給 A 發送(Sign, sid, m), 并將 A 的響應(Signature, sid, m, σ)轉發給FOTS。

3) 當 A 發送(Broadcast, sid, m, σ), S發送(Broadcast, sid, m, σ)。當從 FREG收到(Registered, sid,v), S轉發給A。

當已被攻陷的B收到(Broadcast, sid, m)后, S從FBAUTH獲得這個值并為A仿真FOTS和FREG。

1) 當從FOTS獲得(KeyGen, sid), S發送(KeyGen,sid) 給A, 然后將A的響應(VerificationKey, sid, v0)轉發給FOTS。

2) 當從 FOTS收到(Sign, sid, m)后, 給 A 發送(Sign, sid, m), 并將 A 的響應(Signature, sid, m, σ)轉發給FOTS。當從FREG收到(Registered, sid, v), 轉發給A (v可以不等于v0)。

Simulating the recipient

當A發送(Broadcasted, sid, m, σ)給R時, S為A仿真協議πBAUTH。

1) 如果 v =⊥, 為 A仿真來自 FREG的消息(Retrieve, sid)。當A響應后, 從FREG獲得(Retrieve,sid, v’)。如果 v’=⊥或者存在記錄(m’, v’), 不做任何行動; 否則令v = v’。

2) 當從FOTS收到(Verify, sid, m, σ, v), 給A發送(Verify, sid, m, σ, v), 隨后將A的響應轉發給FOTS。

3) 如果 FOTS輸出(Verified, sid, m, σ, f = 1)給 R,記錄(m, v)并將來自FBAUTH的(Broadcasted, sid, m)發送給R。否則, 不做任何行動。

Simulating party corruption

當A攻陷一個參與方，S也攻陷相應的參與方并將其內部狀態提供給A。

IDEAL和REAL不可區分

定義事件P為：對于消息(Broadcasted, sid, m,σ)，當接收者從 FOTS收到(Verified, sid, m, σ, f=1)，而 B在消息傳輸的時刻尚未被攻陷且從未發送過(Broadcast, sid, m, σ)。然而，根據 FOTS和FREG，事件P不會發生。原因如下：首先，接收者會從 FREG獲得一個正確的驗證密鑰(否則，FOTS不會發送(Verified, sid, m, σ, f = 1))；然后，如果 B未被攻陷且未發送(Broadcasted, sid, m,σ)，那么消息m不會被FOTS簽名。因此，R會從FOTS收到(Verified, sid, m, σ, f = 0) (否則，與 FOTS的EU-COMA相矛盾)。

由于事件P不會發生，因此上述仿真是完美的，即 πBAUTH在(FOTS, FREG)-混合模型下安全實現了理想函數FBAUTH。 □

5 結束語

本文在UC框架研究了基于一次簽名廣播認證協議。首先，設計了一次簽名理想函數FOTS并提出了UC安全的一次簽名協議HORS+。與HORS相比，HORS+的安全依賴于較弱的安全假設。其次，給出了廣播認證理想函數 FBAUTH，在(FOTS, FREG)-混合模型下構造了 UC安全的廣播認證協議πBAUTH。根據組合定理，利用HORS+構造的組合協議在 FREG-混合模型下可以安全實現理想函數FBAUTH。

[1] CANETTI R. Universally composable security: a new paradigm for cryptographic protocols[EB/OL]. http://eprint. iacr.org/2000/067.

[2] 李鳳華, 馮濤, 馬建峰. 基于VSPH的UC不經意傳輸協議 [J]. 通信學報, 2007, 28(7):28-34.LI F H, FENG T, MA J F. Universally composable oblivious transfer protocol based on VSPH[J]. Journal on Communications, 2007,28(7):28-34.

[3] LAMPORT L. Constructing Digital Signatures From a One-Way Function[R]. Technical Report SRI-CSL-98, SRI International Computer Science Laboratory, 1979.

[4] PERRIG A. The BiBa one-time signature and broadcast authentication protocol[A]. ACM Conference on Computer and Communications Security[C]. 2001. 28-37.

[5] MITZENMACHER M, PERRIG A. Bounds and Improvements for BiBa Signature Schemes[R]. No. TR-02-02, Computer Science Group,Harvard University, USA, 2002.

[6] REYZIN L, REYZIN N. Better than BiBa: short one-time signatures with fast signing and verifying[A]. Information Security and Privacy,7th Australian Conference, ACISP 2002[C]. 2002. 144-153.

[7] PIEPRZYK J, WANG H X, XING C P. Multiple-time signature schemes against adaptive chosen message attacks[A]. Selected Areas in Cryptography, SAC 2003[C]. 2003. 88-100.

[8] PARK Y, CHO Y. Efficient one-time signature schemes for stream authentication[J]. Journal of Information Science and Engineering 22,2006.611-624.

[9] LUK M, PERRIG A, WHILLOCK B. Seven cardinal properties of sensor network broadcast authentication[A]. ACM Workshop on Security of Ad Hoc and Sensor Networks, (SASN’ 06)[C].2006.

[10] CANETTI R. Universally composable signatures, certification, and authenticated communication[A]. Proceedings of 17th Computer Security Foundations Workshop[C]. 2004.

[11] GOLDREICH O. The Foundations of Cryptography[M]. Cambridge University Press, 2001.