遺傳算法在箱體零件CAPP數控加工工步排序決策中的應用研究

劉曉陽，劉恩福，方憶湘，李宗斌

LIU Xiao-yang1, LIU En-fu1, FANG Yi-xiang1, LI Zong-bin2

（1.河北科技大學 機械電子工程學院，石家莊 050024；2.西安交通大學 制造系統國家重點實驗室，西安 710049）

0 引言

機械制造中，箱體零件由于品種多樣、結構復雜、生產狀態模糊和生產環境復雜，使得工序工步排序變成為極其復雜的決策過程。在現代數控加工中，一般工序數目較少，而一個工序內工步數目較多，此時工步排序則變得更復雜、更詳細。本文使用遺傳算法解決了CAPP中加工工步的優化排序，在文獻[4]的基礎上，目標函數由換刀時間、工作臺轉位時間和刀具在三個坐標軸方向快速移動到加工區域所需要的時間組成。并利用多色集合理論將工步排序的約束規則以圍道布爾矩陣的形式存儲，根據不同的加工對象，通過添加約束規則確保工步之間的約束順序。

1 工步排序的數學模型

工步排序的數學模型可描述為[4]：

設S={s1,s2,…,sn}是某工件在加工中心上一次裝夾的n(n>1)個加工工步的集合，S有n個元素， 所以存在n！種工步順序，這n個工步構成某一種工序順序x={o1,o2,…,on}。通過進行優化找一個最優的順序x*，能夠滿足要求的約束規則，并且使換刀、工作臺轉位的輔助時間和刀具在三個坐標軸方向快速移動到加工區域所需要的時間最短。因此，目標函數f(x)由三部分組成：

每次換刀時間為tT，若順序x中工步ai使用的刀具為Di，則順序x的換刀時間f1(x)：

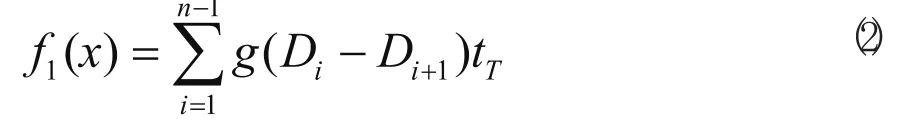
式中g(*)的取值如式(3)：

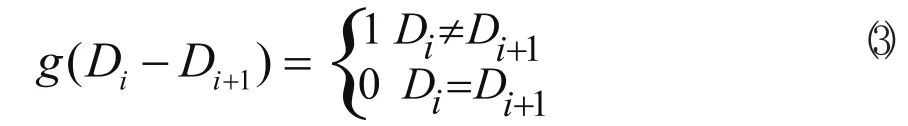
工作臺轉位90°需要的時間為t'i，若順序x中相鄰工步i和i+1之間工作臺轉過角度Ai，則順序x的工作臺轉位時間f2(x)：

假設從工步oi到oi+1，刀具在3個坐標軸方向快速移動到加工區域所需要的時間ti,i+1，刀具快速移動的時間與刀具移動的距離有關，f3(x)可以表示為：

優化目標是尋找一種最優的工步順序x*，使

2 加工中心上工步排序問題的約束模型

2.1 建立關系模型

多色集合理論（Theory of polychromatic Sets，TPS）[4,5]是俄羅斯的Pavlov V.V.教授于1995年提出的。它是一種新的信息處理工具。利用多色集合理論建立零件特征、工步排序的約束規則與加工工步、面孔屬性之間的關系模型，如圖1所示；零件特征與工步排序的約束規則之間的關系模型，如圖2所示。前者把工步排序中的各個工步、面孔屬性作為多色集合的設計元素，將加工零件特征和需要添加的約束規則作為多色集合的統一顏色，后者將工步排序的約束規則作為多色集合設計元素，將加工零件特征作為多色集合的統一顏色，建立了工步排序過程的網絡數學模型，形成圍道組成矩陣[A×F(A)]和[F(Ai)×F(Aj)]。

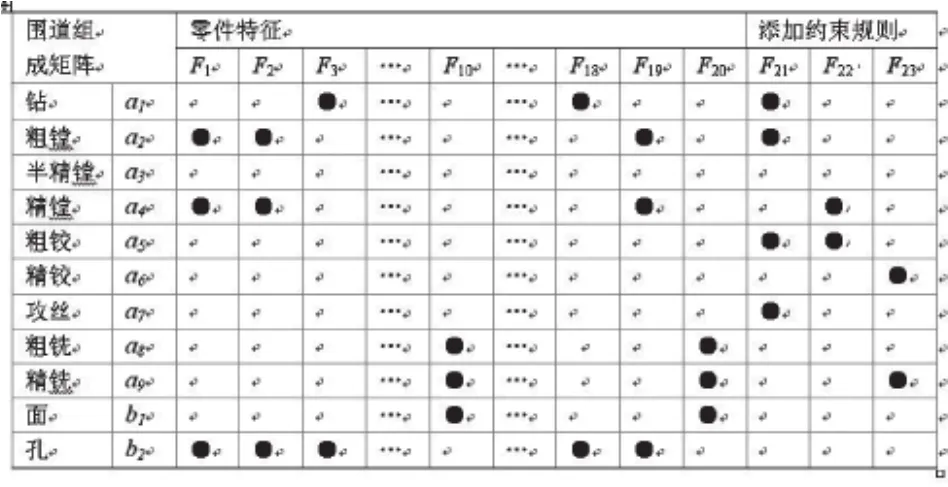
圖1 圍道組成矩陣[A×F(A)]

圖2 圍道組成矩陣[F(Ai)×F(Aj)]

假設一條加工路線由9個加工工步組成，分別是a1,…,ai,…,a9，面孔屬性分別表示為b1 和b2，集合A數學表達式為：A=(a1,…,ai,…,a9,b1,b2)。

顏色集合F(A)由零件特征和添加的約束規則組成，假設某零件由有編號為1～20的特征，每個特征的加工工步鏈如下：通孔1、2、5、8、11、16、19：粗鏜—精鏜；平面4、7、10、13、15、17：粗銑—精銑；螺紋孔系3、6、9、12、14 、18、20：鉆。

在圖1中表示成ai和Fj對應的單元格中為“●”就表示了顏色Fj（A）和元素ai的顏色Fj（ai）。可查找 到具有“相鄰約束”的工步類型并以表1的形式彼此之間可能存在約束關系。

表1 具有“相鄰約束”的工步類型之間的約束關系

表1中●表示豎列和橫列的工步類型之間存在關聯，對應的橫列的工步類型在前，豎列的工步類型在后。在表1中可以看到a1和a2之間存在“相鄰約束”關系；在表中a5和a7也含有“相鄰約束”關系，但只存在a5a7，并且a5和a7有先后的約束要求，也就說在加工過程中存在工步類型a5要先于a7進行加工。

在圖2中， F21、F22、F23表示成工步關聯關系分別為oioj、om^on和(ol,ok)。 oioj表示oi和oj在工步排序中相鄰，om^on表示om和on不相鄰，(ol,ok)表示ol排在ok的前面，ol和ok不相鄰約束。

2.2 基于關系模型獲得相關聯的工步

通過上面建立的關系模型，找到彼此之間相關聯的工步并以布爾矩陣的形式進行存儲，過程如下：

1）通過圖2找到約束要求Fj對應的特征Fi。

2）通過如圖1所示布爾矩陣找到約束要求Fj對應的工步類型ai。

3）通過Fi和ai可以找到工步oi，oi即為含有約束要求Fi的工步，同樣可以找到與oi相關聯的工步oj。

3 利用遺傳算法進行工步排序

3.1 通過編碼產生初始種群

編碼采用實數編碼的方式，通過編碼產生初始種群。設有n個工步，則基因值為在1～n之間隨機取值，且每個基因值不同。假設有u個特征，v種加工方法，w種約束規則。將類似圖1的數據存入二維數組a[v][u+w]中，具體編碼過程如圖3所示。

圖3 編碼產生初始種群的流程圖

按照圖3進行編碼得到的染色體都滿足先粗后精、先面后孔的約束條件，每一條染色體代表一個合理的加工順序。

3.2 交叉操作

設需要進行交叉操作的兩個父代個體為A1、A2，它們交叉之后產生的子代個體為B。隨機產生兩個交叉位置e1、e2，設e1

交叉操作是GA產生新個體的主要方法，所以交叉概率一般應取較大值。但若取值過大又會破壞群體中的優良模式；若取值多小，產生新個體的速度又較慢。一般建議的取值范圍是0.4～0.99。

3.3 變異操作

變異操作采用啟發式互換式變異，即隨機選取一個基因位置，判斷該位置的基因能不能與前面或者后面的基因值互換，判斷過程中需要利用約束模型。

變異概率是增加種群多樣性的重要因素，太小則不會產生新個體，太大則使遺傳算法成為隨機搜索。由于本算法的變異操作具有非強制性，而是滿足相應的條件才執行，所以變異概率不宜取太小，在0.2～0.9之間為宜。工步數目較少時，交叉概率和變異概率取較大值；反之，取較小值。

4 實例

圖4是一個箱體類零件，基于建立的關系模型利用遺傳算法對箱體零件的加工工步進行排序。該箱體零件需要加工20個特征，主要是孔系的加工，方位面分為后面、左面、前面、右面和頂面。

進行工步排序前，首先添加約束規則和參數的設置。獲得零件特征所在方位面及對應的加工工步，進行約束規則的添加，獲得添加約束的工步。取遺傳算法運行參數的群體大小為101，交叉概率為0.75，變異概率0.85，最大進化代數為120。每次換刀時間為5秒，工作臺轉位90°所需時間為2秒，可通過工步排序取得最優解。所得結果滿足工步排序受到的條件約束，即先粗后精、先面后孔，且能較快地得到較優的排序結果，能夠較大程度地實現方位集中和刀具集中。

圖4 箱體零件模型

5 結論

本文主要解決數控加工中心上箱體零件一次裝夾下的工步排序優化問題。利用多色集合理論建立了加工中心上工步排序問題的約束模型，在進行工步排序過程中，能夠根據零件的實際的加工要求靈活的添加約束規則，利用上述遺傳算法尋求工步順序的近優方案。本文所提出的方法同樣可以解決其它零件工藝路線的決策問題。

[1] 蒲建,王先逵,吳丹.工藝規劃中的組合優化問題[J].清華大學學報,1997,37(8)：69-71.

[2] 秦寶榮,王寧生.基于遺傳算法的加工中心工步排序優化方法[J].中國機械工程,2002,13(18)：1531-1533.

[3] 秦寶榮,柯文,王寧生.基于遺傳算法的箱體零件加工路線決策方法研究[J].中國機械工程,2002,13(24)：2071-2075.

[4] 郝建波,李宗斌,趙麗萍.加工中心上工步排序問題的約束模型及其遺傳算法求解[J].西安交通大學學報,2008,7(7)：860-864.

[5] 李宗斌.先進制造中多色集合理論的研究及應[M].北京：中國水利水電出版社,2005.