Mellor-Yamada模型在波浪邊界層中的運用

陳杰，蔣昌波，劉虎英，鄧斌

（1. 長沙理工大學水利工程學院，湖南 長沙 410004；2. 湖南省水沙科學與水災害防治重點實驗室，湖南 長沙 410004;3. 湖南省交通規劃勘查設計院，湖南 長沙 410008）

Mellor-Yamada模型在波浪邊界層中的運用

陳杰1,2，蔣昌波1,2，劉虎英1,3，鄧斌1

（1. 長沙理工大學水利工程學院，湖南 長沙 410004；2. 湖南省水沙科學與水災害防治重點實驗室，湖南 長沙 410004;3. 湖南省交通規劃勘查設計院，湖南 長沙 410008）

利用Mellor-Yamada 2.5階封閉格式建立一維垂線波浪邊界層數學模型，利用有限元方法求解，模擬線性波作用下的層流邊界層和喬治沙洲南側海岸一側點的波浪邊界層流速分布，并同理論或其他的計算方法進行比較，結果顯示該模型具有較高的精度，能廣泛運用于波浪邊界層的研究中。

Mellor-Yamada模型；邊界層；數值模擬

波浪邊界層存在于海底床面附近，雖然厚度只有2～10 cm，但其水流運動特性與波浪的傳播和變形、泥沙起動以及床面形態的變化密切相關，流體內部紊動結構、波浪底部摩阻力、波浪的質量輸移速度、波能衰減、波浪要素變化、波浪作用下的底沙起動輸移、懸沙分布及其輸送的合理確定等，都直接或間接的與波浪作用下的底部邊界層有關。自Jonsson[1]和Sleath[2]的工作以來，人們已經進行了很多關于波浪邊界層的理論、數值和實驗方面的研究工作。如趙子丹[3]等將大渦模擬法簡化為二維形式，利用SGS格子渦模型封閉二維Navier-Storkes方程水流運動方程組,得到平底振蕩流邊界層立面二維水流數值模型，討論了振蕩流邊界的紊動特性沿垂線分布和隨相位變化的情況。蔣昌波[4]等建立了立面二維曲線坐標下的數值模型，模擬波浪作用下底層分離渦隨時間、空間變化的動力特性，對底層流動的紊動特性、床面剪切應力的隨時間、空間的變化以及渦動結構的尺度分別進行了討論。孫亞斌[5]等利用格子Boltzmann方法中不可壓縮的模型模擬了線性波和橢圓余弦波作用下的層流邊界層流速變化情況，程永舟[6,7]等研究了橢圓余弦波作用下的非對稱沙紋上的流動特性。然而，由于波浪邊界層的復雜性，波浪邊界層的問題仍然需要深入研究。

Mellor和Yamada[8,9]提出一種層次化的封閉模型，即Mellor-Yamada模型（以下簡稱MY模型）。Mellor-Yamada模型用紊動能量(Turbulent energy)和紊動特征長度(Turbulent length scale)參數表示，共分成了5個等級。MY模型的優點是使用很少的封閉所需常數。MY模型已經廣泛的運用與大氣[10,11]和海洋[12-14]的計算。許多學者對MY模型進行改進、推廣和運用。萬振文[15]等將MY閉合模型推廣應用到生態動力學模型方程的二階湍封閉過程中。李華軍[16]等探討Mellor-Yamada模型考慮泥沙的影響，進而再將其用于河口地區泥沙輸移的探索和研究。本文將MY模型運用于波浪邊界層問題的研究，建立利用Mellor-Yamada 2.5階封閉模型的一維垂線邊界層數學模型，并用于波浪邊界層問題的研究。

1 模型基本理論

1.1 基本方程

一維垂線邊界層數學模型的基本方程為符合傳統靜力學假設的淺水方程。動量守恒方程和能量守恒方程中的雷諾湍動和通量項都用參數化的渦擴散率表示，動量方程中考慮科氏力的作用，水平變量和垂直面水平對流忽略不計。

連續方程為：

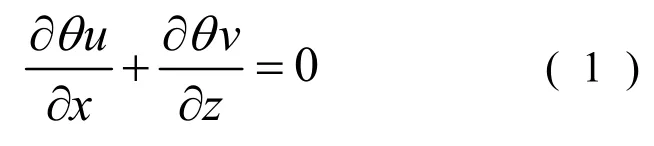
動量方程為：

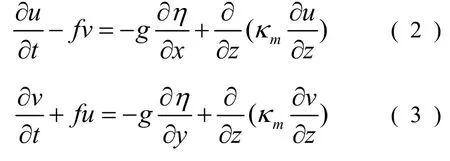
能量守恒方程為：

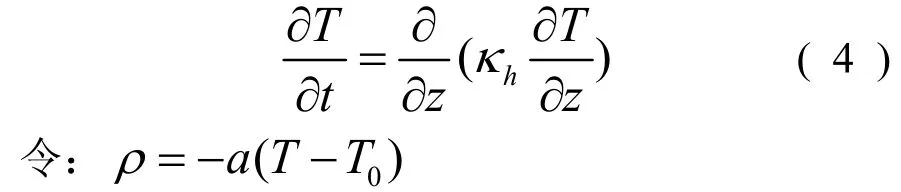
則能量守恒方程可以寫成：

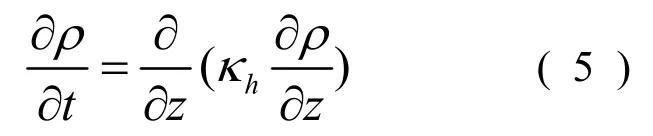
1.2 邊界條件

在自由邊界，使用風壓力wτ和熱流通量˙H都源于水平動量和能量，分別為：

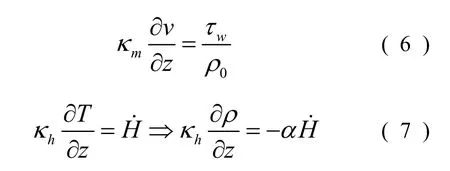
在底部邊界，假設剪應力τb為常數，摩阻流速u*與剪應力的關系為：

則對數流速分布為：

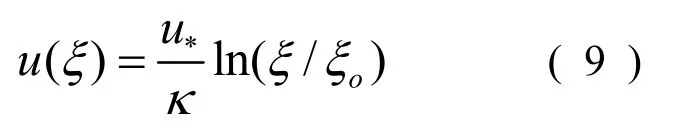
底部滑移條件時，定點速度用剪應力粗糙高度表示：

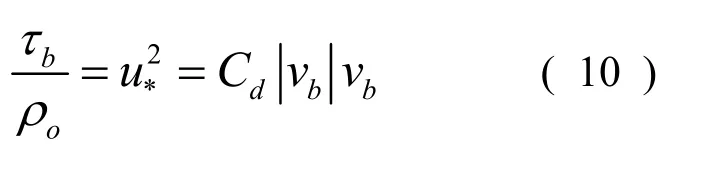
由 (8)(9)(10) 式得到阻力系數：

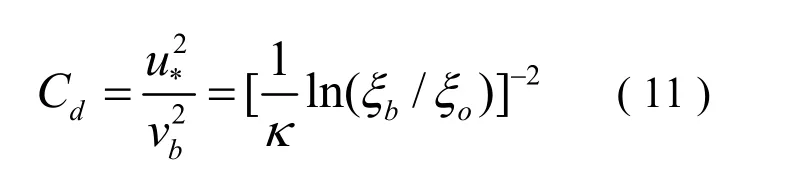
因此得到：

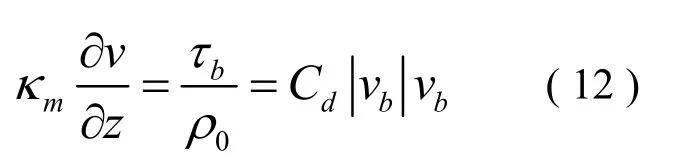
在自由水面，紊動能量與紊動特征長度有：

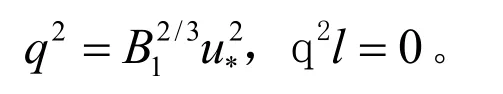
1.3 Mellor-Yamada 2.5階封閉模型

Mellor-Yamada 2.5階封閉模型將紊動動能(turbulent kinetic energy)和紊動特征長度(turbulent master length scale)引入守恒方程。盡管計算引入參數，但是考慮到這些參數的瞬時性和空間演變性，因此其具有很多優點。Mellor和Yamada[9]將守恒方程寫成紊動動能和紊動特征長度的形式：

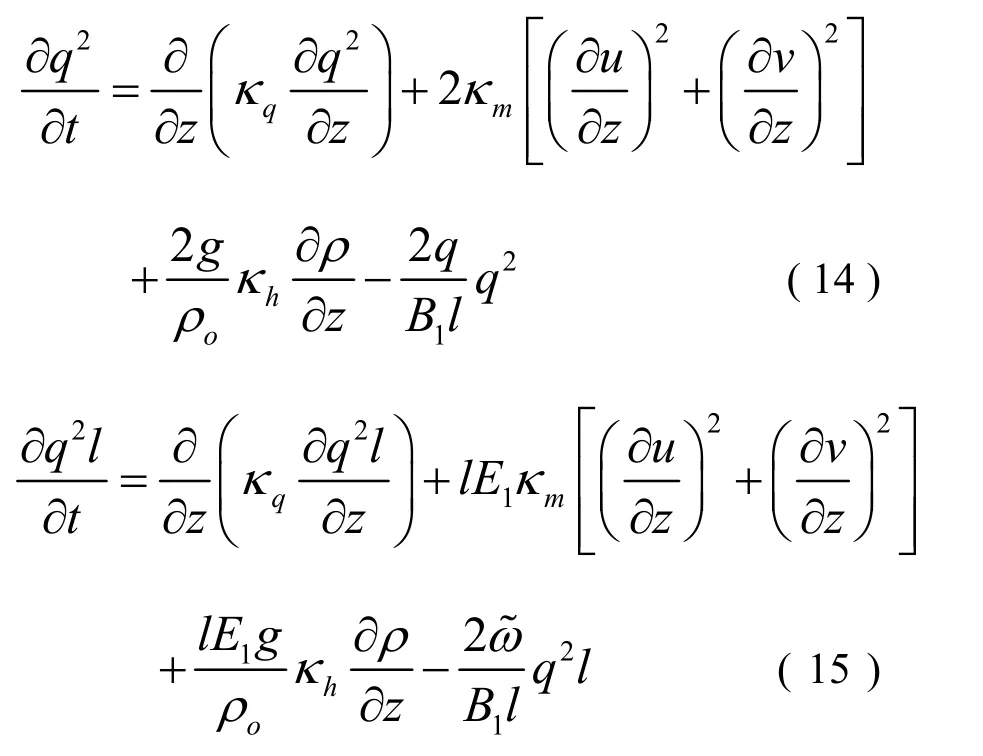
紊動粘性系數mκ，紊動擴散系數hκ，紊動量擴散系數qκ的確定如下式：

式中，E1，E2分別取1.8，1.33；A1，B1，A2，B2，C1，Sq，S1是與主控的紊動特征長度和紊動結構特征有關的實驗常數，分別取0.92，16.6，0.74，10.1，0.08，0.2，0.2。

1.4 數值方法

模型采用有限元方法進行求解，利用均勻網格進行離散。

2 模型運用及結果討論

2.1 線性波作用下的層流邊界層

層流邊界層內的流體運動方程為：

式中：u為邊界層內任一點的流速，p為邊界層內任一點的壓力， 為邊界層內任一點的剪切應力。

由微幅波理論，近底質點水平速度為：

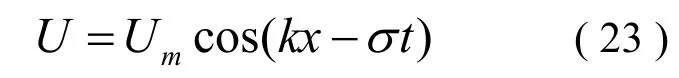
式中，Um是近底波浪水質點水平速度的最大值，k是波數，ω是波浪角頻率

于是線性波作用下邊界層內任一點流速為：

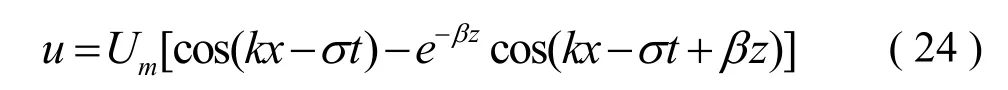
圖1給出的線性波（波高0.10 m，周期1.6 s，水深0.40 m）作用下一個周期內床面附近的水平流速分布的數值模擬結果和理論值，橫軸坐標為u/ Um，縱軸坐標為z/δ，兩個都是無量綱的量，δ為朗吉特-希金斯定義的邊界層厚度其中，實線為理論值，圓點為數值模擬值。可以看出數值模擬結果十分逼近理論結果。特別是在t0， ，2π附近，也就是邊界層流速達到最大值時，兩個結果吻合良好。在tπ/2和3π/2附近，在靠近海床的地方數值模擬值略小于理論值，兩者最大誤差在5%以內。運用朗吉特-希金斯定義的邊界層厚度求得理論邊界層厚度δ為0.713 6 mm，將數值模擬結果運用Jonsson[1]提出的方法求得邊界層厚度d為0.709 5 mm，誤差為0.6%。因此，該模型能很好的運用于線性波作用下層流邊界層流場問題的研究，且具有較高的精度。

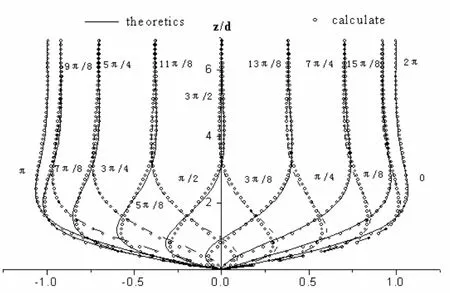
圖1 線性波作用下層流邊界層流速分布Fig. 1 Velocity distributions in laminar flow under linear wave

2.2 喬治沙洲海岸波浪邊界層

圖2給出喬治沙洲南側海岸一側點的波浪邊界層流速分布，海岸受到M2潮汐和0.095 5 Pa風的作用，風向為偏北118.5°[17]。設u方向為正北方向，橫軸為流速，縱軸為水深，實線為Mellor-Yamada方法計算值，圓點為Davies和Furnes[18]提出二次渦粘性封閉格式(Quadratic Eddy Viscosity Closure)的計算值。可以看出兩者計算結果比較接近，因此，該模型能很好的運用于波浪作用下邊界層流場問題的研究，且具有較高的精度。

圖2 喬治沙洲海岸波浪邊界層流速分布Fig. 2 Velocity distributions on the southern flank of Georges Bank

3 結 論

本文引進Mellor-Yamada 2.5階封閉格式建立一維垂線波浪邊界層數學模型，利用有限元法進行求解，模擬線性波作用下的層流邊界層，并同理論值進行比較，模擬喬治沙洲南側海岸一側點的波浪邊界層流速分布，并且同其他學者提出的計算方法進行比較，結果顯示該一維垂線數學模型具有較高的精度。

同時，由于實際海洋環境中波浪作用是隨機的，因此利用該數學模型模擬隨機波浪作用下的邊界層流動結構更加具有實際意義，將成為我們下一步工作的重點。本文認為Mellor-Yamada封閉格式具有使用很少的封閉常數，計算快捷、準確等優點，在波浪邊界層及海岸泥沙運動機理等問題的研究中將得到廣泛的運用。

[1] Jounsson I G. Wave boundary layer and friction factor [J]. Proc 10th Conf Coastal Eng ASCE Tokyo, 1966: 127-148.

[2] Sleath J F A. Velocities above rough bed in oscillatory flow [J].Water, Port Coastal Ocean Eng, 1974, 100(WW4): 287-304.

[3] 趙子丹, 蔣昌波, 白玉川. 振蕩流底部邊界層運動的數值研究[J]. 天津大學學報, 2001, 34(5): 568-572.

[4] 蔣昌波, 白玉川, 趙子丹, 等. 波浪作用下沙紋床面底層流動特性研究 [J]. 水科學進展, 2003, 14(3): 332-340.

[5] 孫亞斌, 張慶河, 張金鳳. 振蕩層流邊界層運動的格子Boltzmann模擬 [J]. 水動力學研究與進展, 2006 (5): 347-353.

[6] Cheng Yongzhou, Wang Yongxue, Jiang Changbo. An experimental investigation of the velocity under cnoidal waves over the asymmetric rippled bed [J]. Acta Oceanologica Sinica, 2007, 26 (1):130-139.

[7] 程永舟, 王永學, 蔣昌波, 等. 淺水非線性波作用下沙紋床面底層流動特性試驗研究 [J]. 水科學進展, 2007, 18(6): 801-806.

[8] Mellor G, Yamada Y. A hierarchy of turbulence closure models for planetary boundary layers [J]. Journal of the Atmospheric Sciences,1974, 31(10): 1 791-1 806.

[9] Mellor G, Yamada Y. Development of a turbulence closure model for geophysical fluid problems [J]. Reviews of Geophysics and Space Physics, 1982, 20(4): 851-875.

[10] Yamada T. Anumerical experiment on pollutant dispersion in a horizontally-homogeneous atmospheric boundary layer Atmos [J].Environ, 1977, 11: 1 015-1 024.

[11] Yamada T, Bunker S. Anumerical model study of nocturnal drainage flows with strong wind and temperature gradients [J]. Appl Meteorol, 1989, 20: 545-554.

[12] Kantha L H, Clayson C A. An improved mixed layer model for geophysical applications [J]. J Geophys Res, 1994, 99: 25 235-25 266.

[13] Mellor G L. One-dimensional, ocean surface layer modeling: a problem and a solution [J]. J Phys Oceanogr, 2001, 31: 790-809.

[14] 魏皓, 武建平, 張平. 海洋湍流模式應用研究 [J]. 青島海洋大學學報, 2001, 31(1): 7-13.

[15] 萬振文, 袁業立. 海洋浮游生態系統連續介質動力學模型湍封閉研究 [J]. 水動力學研究與進展, 2001, 15(2): 229-239.

[16] 李華軍, 梁丙臣, 李東永, 等. 懸對沙Mellor-Yamada海洋邊界層模型計算結果的影響 [J]. Marine Sciences, 2004, 28(1): 27-32.

[17] Naimie C E, Loder J W, Lynch D R. Seasonal variation of the three-dimensional residual circulation on Georges Bank [J].Geophys Res, 1994, 99(C8): 15 967-15 989.

[18] Davies A M, Furnes G K. Observed and computed M2 tidal currents in the North Sea [J]. Phys Oceanogr, 1980, 10: 237-257.

Study of wave boundary layer based on Mellor-Yamada model

CHEN Jie1,2, JIANG Chang-bo1,2, LIU Hu-ying1,3, Deng Bin1
(1. School of Water Conservancy, Changsha University of Science & Technology, Changsha 410114, China;2. Hunan Province Key Laboratory of Water, Sediment Sciences & Flood Hazard Prevention, Changsha 410114, China;3. Hunan Provincial Communications Planning, Survey & Design Institute, Changsha 410008, China)

The one dimension time-stepping point numerical model which uses linear finite elements to determine the vertical structure of the horizontal components of velocity under wave forcing is given. And the velocity distributions in laminar flow under linear wave and on the southern flank of Georges Bank are presented. Compared with theoretic and other numerical models, the numerical result shows result is good and that the numerical model is able to investigate the wave boundary layer problem.

Mellor-Yamada model; wave boundary layer; numerical simulation

P731.22; TV139.2

A

1001-6932(2010)03-0253-04

2008-12-08；收訂日期：2009-10-30

國家自然科學基金資助項目（No.50979008,50909009），水沙科學與水災害防治湖南省重點實驗室基金資助

陳杰（1982－），男，助教，博士生，主要從事河流、海岸動力過程及其模擬技術的研究。電子郵箱：chenjie166@yahoo.com.cn