一種化學氣相淀積過程溫度控制的新算法

張 慧, 袁德成

(沈陽化工大學信息工程學院,遼寧沈陽 110142)

一種化學氣相淀積過程溫度控制的新算法

張 慧, 袁德成

(沈陽化工大學信息工程學院,遼寧沈陽 110142)

以化學氣相淀積過程中晶圓表面溫度分布為研究對象,分析反應過程中的工藝特點及動態特性,針對傳統機理建模難以準確預測、控制晶圓表面溫度的發展變化,提出基于線性二次優化的控制算法,由系統給定的輸入及初始條件,計算出系統的響應來預測未來軌跡,通過仿真演示了控制器的控制性能.

化學氣相淀積 ; 溫度控制; 線性二次優化; 預測軌跡

集成電路是由多層被精細刻畫過的薄膜組成,每層都用化學的方法改變其構造以達到期望的電子特性.盡管集成電路的設計一般由電子工程師來完成,但這些設計的制造要經過一系列的物理和化學操作單元來實現.主要的操作單元有清洗、光刻、離子注入、刻蝕、熱處理、化學氣相淀積(CVD),物理氣相淀積、分子束外延、電鍍、化學機械研磨、晶圓測試等,其中的一些過程都是在原子或分子級進行操作,任何一個環節出錯,都會影響產品的質量.在芯片制造過程中,大部分所需的薄膜材料,不論是導體、半導體、或是介電材料,都可以用化學氣相淀積來制備,它具有淀積溫度低,薄膜成分和厚度易控,均勻性與重復性好,階梯覆蓋好,操作方便等優點.其中淀積溫度低和覆蓋性好對超大規模集成電路的制造十分有利,因此它是目前集成電路生產過程中最重要的薄膜淀積方法.目前最常用的方法有常壓化學氣相淀積、低壓化學氣相淀積以及等離子體增強化學氣相淀積等.

化學氣相淀積過程是一個非常復雜的非線性過程,其實質是指含有薄膜所需的原子或分子的化學物質在反應室內混合并在氣態下發生反應,其原子或分子淀積在晶圓表面聚集,形成薄膜.淀積過程中反應爐內將發生 4種類型的化學反應,并伴隨著低壓,超真空,化學反應與傳遞現象同時發生等特點,反應爐內部的復雜性導致對其有效控制十分困難.長期以來,國內外研究人員針對化學氣相淀積過程中的化學反應和傳遞現象,建立了多種數學模型及控制方法,其中主要有Middleman與 Hochberg從化學工程角度提出的不同建模方法[1];Badgwell等概括了 CVD過程的建模和控制問題[2];Edgar提出了基于模型的 run-to-run控制[3];以上提出的控制算法都是基于模型的控制算法,這些模型在理論上對于揭示反應爐內部的現象起到一定的積極作用,然而化學氣相淀積過程參數多且過程復雜,很難建立精確的機理模型,在控制上呈現出一定的局限性.本文針對化學氣相淀積過程中控制的難點,在分析CVD工藝和動態特性的基礎上,求解溫度分布動態模型,構造出數據平臺,結合線性二次優化的控制算法,根據系統溫度分布的真實輸入及初始值,計算出系統的響應來預測系統的軌跡,取得了良好的控制效果.

1 CVD工藝簡介及其數學模型

化學氣相淀積是一個由氣相物質傳遞 (通過對流和分子擴散)、均相或非均相化學反應以及熱量傳遞組成的復雜系統.要獲得具有一定化學組成、純度高、結構完整、物理性能優良和均勻的薄膜,必須對淀積過程中的機理、特性及相互影響作深入研究.

化學氣相淀積過程系統如圖 1所示.以 H2與WF6發生的鹵化還原反應為例,描述其工藝:晶圓被水平放置在石英托盤上,WF6通過墻上的狹縫中注入反應室,鹵素燈在反應室的頂部透過石英窗給晶圓加熱,H2與WF6在反應室內混合并在氣態下發生反應,其原子或分子晶圓表面聚集,形成薄膜沉積在晶圓表面.其中溫度是影響薄膜淀積速率,均勻性及平整性的重要參數,實驗重點研究反應爐內的溫度分布.

圖1 CVD過程系統框圖Fig.1 The schematic diagram of the CVD reactor chamber

為充分了解化學氣相淀積特點,合理設計反應器結構,正確選擇操作條件,研究人員對化學氣相淀積過程的數學模型進行了大量研究.文獻[4]中給出了化學氣相淀積過程的模型推導過程,傳熱參數的選擇以及反應堆的相關介紹.用能量守恒方程來描述 CVD過程的動態特性:

公式(1)中右邊第一項代表位置方向上的熱量傳導,第二項表示晶圓表面與環境之間的熱量傳遞,它的初始值為零.符號R表示保護環的半徑,Rw表示晶圓半徑.Qother表示所有熱量傳遞的總和,它包括燈的熱量Ql,晶圓和反應室溫度交換Qc,以及晶圓和反應氣體之間的熱傳遞Qg,即

其中,加熱燈的熱量控制器u(t):0≤u(t)≤1.為獲得晶圓表面溫度的動態解,假設晶圓表面的初始溫度為 300 K,加熱燈的熱量為 5 000 W/ m2,用MATLAB的 pdepe指令編寫微分方程函數文件,初始條件函數文件,邊界條件函數文件,求解(1)式中的偏微分方程,得到晶圓表面溫度隨時間t及位置x的分布情況,如圖 2,圖 3所示.采集 500組數據,構建數據平臺,為控制器設計提供數據wd及初始條件.

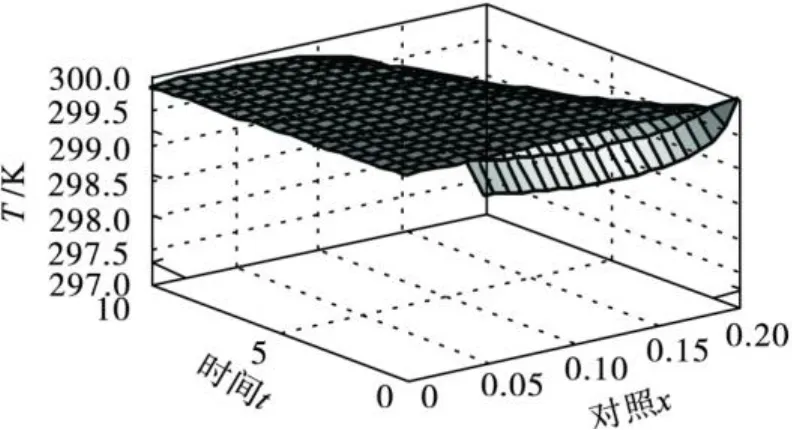
圖 2 晶圓表面溫度分布Fig.2 The temperature distribution at the wafer surface

圖 3 當u(t)從 1變為 0時溫度與位置的關系Fig.3 Relationship of temperature and position whenu(t)changes from 1 to 0.

2 基于線性二次數據驅動的控制器設計

2.1 線性二次軌跡問題

首先介紹線性二次軌跡問題[5]:線性二次軌跡問題的目標是選擇控制的輸入,使對象B的最優軌跡服從二次誤差準則:

式中給定參考軌跡 wr∈,Φ∈,是一個正定加權矩陣,Tr是軌跡的范圍.

給定條件如下:

(1)線性時不變系統 B的軌跡 wd= (wd(1),…,wd(T));

(2)參考軌跡 wr=(wr(1),…,wr(Tr));

(3) 初始軌跡 wini= (wint(1),…, wini(Tini))∈B;

找到對象 B的最優軌跡 w＊∈B,使目標函數‖wr-w‖最小,即解決問題:

2.2 基于線性二次優化的溫度控制

由采集的溫度輸入輸出數據 wd=[u y],通過實現計算系統狀態空間表達式的算法[5],辨識出系統的狀態空間表達式參數 (A,B,C, D).計算系統的狀態空間表達式[6]為:

輸入:ud,yd,lmax,nmax.

1.計算出樣本 nmax,lmax+1的自由響應 Y0;

2.將 Y0解為:Y0=ΓXd;

3.解出系統方程的狀態空間表達式參數(A, B,C,D),其中[xd(1)…xd(nmax+m+1)]:=Xd.

輸出:狀態空間表達式參數 (A,B,C,D).一旦系統輸入輸出表達式的參數 (A,B,C, D)被確定,則由

兩式可計算出系統的初始條件:

如果狀態空間表達式及初始狀態確定了,那么線性二次軌跡演變為解決如下的問題:

式(6)的解為

由式 (7)可計算出優化系統的溫度:

3 仿真結果與驗證

被控對象晶圓溫度系統階次 n=2,輸入m=1,輸出 p=1,樣本大小 N=200,參考軌跡wr=0,針對擾動大小為 ±25%的情況進行仿真.仿真結果如圖 4所示,此時加熱燈能量控制器u(t)=1.

圖 4 晶圓表面溫度分布(u(t)由 0變為 1)Fig.4 The temperature distribution on the w afer surface(u(t),from0to1)

將反應器內加熱燈的能量控制器 u(t)由 1變為 0,仿真結果如圖 5所示.

圖 5 晶圓表面溫度分布(u(t)由 1變為 0)Fig.5 The temperature distribution on the w afer surface(u(t),from1to0)

在時間 t=50s時,對系統加階躍響應,仿真結果如圖 6所示.由以上仿真結果可以看出,當系統存在擾動時,使用數據驅動控制算法計算出wf能夠及時地控制及預測系統的未來軌跡,并能夠計算出預測值 wf與真實數據 wd的誤差僅為 0.019 4.針對以上分析可以看出,在系統存在擾動的情況下,基于數據驅動算法對于控制非常有效,同時具有很好的魯棒性.

圖 6 晶圓表面溫度分布Fig.6 The temperature distribution on the wafer surface

4 結 論

基于線性二次優化的溫度控制算法能夠很好地反映晶圓表面溫度分布的變化,能夠及時跟蹤溫度的變化,具有很好的魯棒性.針對化學氣相淀積過程中控制的復雜性,傳統的機理建模難以準確預測、控制晶圓表面溫度的發展變化,基于線性二次優化的控制方法具有精度高,魯棒性強等優點.目前研究的基于數據驅動的控制方法都是基于被控對象的軌跡是精確的,以及被控對象是低階線性時不變系統的假設之下,而在實際生產中,系統是時變且有噪聲的,因此獲得數據驅動控制的優化算法是以后要研究的目標.

[1] H itchm an M L,Jensen K F.Chem ical Vapor Deposition—Principles and Application[M].N ew York: A cadem ic Press Inc.,1993:1300-1320.

[2] Badgwell T A,B reedijk T,Bushm an S G,et al. M odeling and Control of M icroelectronics M aterials Processing[J].Computers and Chem ical Engineering,1995:19(1):1-41.

[3] Edgar T F,CampbellW J,BodeC.M odel-based Control in M icroelectronics M anufacturing[J].Proceedings of the IEEE Conference on Decision and Control,2000,4:4185-4191.

[4] Chen J,Adomaitis R A.An Object-oriented Framework forM odular Chem ical Process Simulation with Sem iconductor Processing Applications[J].Computers and Chem ical Engineering,2006,30:1354-1380.

[5] M arkovsky Ivan,Rapisarda Paolo.On the L inear Quadratic Data-driven Control[C]//Proceedings of the European Control Conference.Kos:[s.n.],2007:5313-5318.

[6] M arkovsky Ivan,W illem s Jan C, Huffel Sanine V an,et al.Exact and Approx im ateM odeling of L inear System s:A Behavioral Approach[M].Leuven: M onographs onM athem aticalM odeling and Computation,2006:113-138.

[7] O verschee P V an,M oor Bart De.Subspace Identification for L inear System s:Theory,Implem entation, Applications[M].Boston:Kluw er academ ic publishers,1996:110-118.

[8] M arkovsky Ivan,W illem s Jan C,M oor Bart D e,A lgorithm s for Determ inistic Balanced Subspace Identification[J].A utom atica,2005,41(5):755-766.

A New Algorithm of Temperature Control for the Chem ical VaporDeposition Processes

ZHANG Hui, YUAN De-cheng
(Shenyang U niversity of Chem ical Technology,Shenyang110142,China)

The dynam ic characteristics of the chem ical vapor deposition process on affection of w afer’s temperature distributions are analyzed in this paper.It is difficult to predict and control the temperature of the w afer by the traditional m odeling approach.A linear quadratic optim al algorithm is presented,and the response of the temperature system is calculated by the given inputs and the initial condition in order to find the optim al trajectory of the system.The control perform ance is dem onstrated through s im ulation.

chem ical vapor deposition; temperature control; linear quadratic; optim al trajectory

TP273

A

1004-4639(2010)03-0275-04

2009-09-14

張慧(1985-),女,安徽黃山人,碩士研究生在讀,主要從事基于統計的質量反饋控制系統的研究.

袁德成(1960-),男,內蒙古人,教授,博士,主要從事計算機輔助過程工程,生化過程建模與優化控制等方面的研究.