數字攝影測量在桁架結構承載變形監測中的應用研究

牛 鵬

（延安大學 西安創新學院，陜西 西安 7 1 0 1 0 0）

數字攝影測量在桁架結構承載變形監測中的應用研究

牛 鵬

（延安大學 西安創新學院，陜西 西安 7 1 0 1 0 0）

在建筑行業中大量使用桁架結構，然而由于其結構復雜，理論分析和數值模擬均無法準確估計其承載受力變形情況，為此，本文提出一種基于數字攝影測量的桁架結構變形監測方法.該方法通過跟蹤粘貼在桁架表面的人工標志點，計算關鍵監測點在不同時刻的位移信息，來了解桁架在承載過程中的整體變形情況，從而為桁架力學性能分析提供定量參考.對該方法涉及的關鍵技術如標志點識別，三維重建，變形點跟蹤等進行了詳細的研究.為了提高攝影測量解算的精度及效率，提出了基于最小二乘法的捆綁調整算法.實驗結果表明，該方法精度基本可以滿足桁架結構變形監測的精度需求，為桁架變形監測提供一條可行的途徑.

桁架結構；變形監測；數字攝影測量

桁架結構廣泛應用于建筑行業，因而對其安全性能的評估至關重要.桁架結構的安全性主要取決于其力學性能.然而，由于試驗分析過程中，桁架結構實驗尺寸大、變形大、應力分布十分復雜的特點，傳統的位移傳感器和電阻應變片等無法滿足大變形測量的需要[1].隨著彈塑性單元和非線性數值解法的發展,以及近年來計算機硬件水平的飛速提高,有限元分析模型逐漸成為主流.然而，由于桁架結構的受力狀態十分復雜，對其進行精確的理論分析尚有很大的難度.

本文提出了一種非接觸式三維光學桁架結構變形觀測的新方法.該方法采用數字攝影測量技術，通過跟蹤粘貼在桁架結構表面的眾多人工標志點，計算標志點三維坐標在不同時刻的位移信息，來分析桁架結構的整體變形情況.為了驗證該方法的有效性，分別進行了精度驗證實驗以及桁架結構變形觀測實驗，并將測量結果與全站儀進行了對比分析.

1 測量原理

物方點經過相機鏡頭攝影后成像到像平面上，理想的投影成像模型是幾何光學中的小孔成像模型，其本質就是射影幾何中的中心透視投影過程.相機實際成像時，由于各種因素的干擾，主點的像平面坐標不嚴格為零，存在一微小值(x 0，y 0)，使得像點在像平面上相對其理論位置存在一定的微小偏差，記為(Δx′，Δy′).實際像點的共線方程可以寫成[2]：

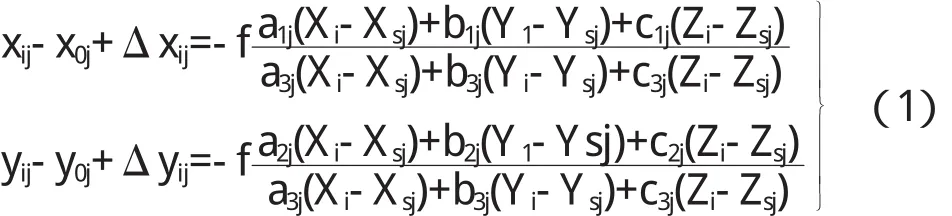
對同一個物方點P來說，在內外方位參數已知的情況下，只要知道P點在2個以上圖像上的二維坐標（x,y），根據公式1列出3個以上的方程構成方程組，就可求解出其在空間中的三維坐標（X，Y，Z）.

2 桁架結構變形測量過程

桁架結構變形測量的流程如圖1所示，首先在關鍵監測點粘貼人工標志點，圍繞桁架結構拍攝照片，保證每個人工標志點至少在5張照片上出現；其次，識別照片中的人工標志點，并根據公式（1）重建人工標志點的三維坐標，用捆綁調整算法進行平差；最后將各個時刻重建的關鍵監測點的三維坐標通過三點坐標對齊法將坐標系歸一，從而計算桁架結構在受力過程中各個時刻的變形量.

2.1 標志點識別及三維重建

標志點包括編碼標志點及非編碼標志點兩種類型.非編碼標志點通常采用黑白相間的顏色，主要考慮標志點自身顏色和背景顏色有盡量大的反差編碼標志點具有唯一的編號，這樣就可以對這些標志點實現自動的檢測與識別.為了簡化圖像處理難度和提高測量的自動化程度，本文采用圓形非編碼標志點及環形人工編碼標志點，如圖2所示.

圖2 人工標志點

圓形標志點經過透視成像后成為橢圓，為了對橢圓進行識別和中心定位，就需要進行圖像處理，一般處理步驟包括：邊緣檢測、亞像素邊緣提取與橢圓中心擬合[3].首先使用C a n n y算子進行邊緣檢測[4]；在結果中搜索可能的橢圓邊界，同時排除不可能的邊緣；對確認為橢圓邊界的圖像點使用梯度均值法進行亞像素修正，然后使用最小二乘法擬合得到橢圓中心和長短軸、旋轉角等信息.

人工標志點識別完成后，即可根據共面方程[3]確定兩幅圖像之間的位置關系.并以此確定世界坐標系，一般情況下將第一幅圖像的坐標系作為世界坐標系.然后依據共線方程[2]確定任意一幅圖像相對于世界坐標系的絕對方位.由于編碼點在每張照片上都顯示其唯一的I D,通過I D可以對其進行匹配.對于非編碼點基于核線約束條件進行匹配[3].由于核線約束是一維約束，而且像點存在誤差，所以僅考慮兩幅圖片時，很容易產生歧義性，利用多幅圖片之間相互進行極線匹配就可以大大降低匹配的出錯率.匹配成功后依據公式（1）列方程即可求解每一個人工標志點的三維坐標.

2.2 基于最小二乘法及自由網平差的捆綁調整算法

將像點坐標記為L,L=(l1,l2,……ln)T，未知量（物體點坐標、相機參數）記為X,X=(X1,X2,…Xu)T.依據共線方程知：真實像點坐標L軌與真實未知量X軒之間的關系可以用函數φ表達為：

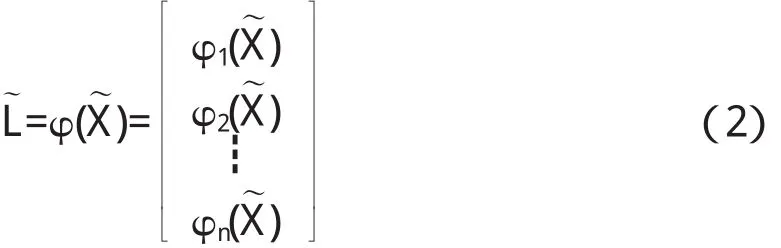
由于像點坐標及未知量的真實值均不可知，于是真實像點坐標L軌可以用觀察值L與一個偏差v之和來表示，未知量真實值X軒用估計值X贊代表，于是，公式（2）可以展開為：

假設未知量的初值為 X0，那么X贊=X0+x贊.如果x贊足夠小，那么公式（3）可以用泰勒公式展開為：

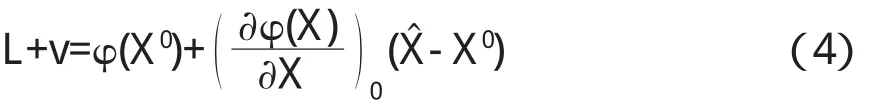
2.3 坐標對齊及變形量計算

各個時刻重建的監測點三維坐標處于自由坐標系中，為了進行變形量計算，需要將各個時刻的坐標進行歸一，本文采用三點法進行坐標系的歸一化.坐標歸一化以后，即可依據公式（6）計算出各個時刻的三維變形量.

其中，(ΔX,ΔY,ΔZ)為變形向量，(Xi,Yi,Zi)為某一監測點在第i時刻的三維坐標，(X1,Y1,Z1)為該監測點在變形前的三維坐標.

3 試驗結果及分析

3.1 精度分析

以某實際桁架為實驗對象，如圖3所示，在關鍵部位粘貼人工標志點，然后用本文方法進行變形監測.首先設置6個關鍵觀測點1-6，及三組距離：1-2、3-4、5-6.在靜止狀態下重復測量6次，實驗結果如表1所示.依據3S i g m a準則知，本文方法的精度可以達到0.8 m m/m.由此可知本文方法完全滿足桁架測量的精度需求.

圖3

表1 三組距離值重復測量6次

3.2 桁架變形測量

為了監測桁架結構變形量，對桁架結構施加載荷，當變形趨于穩定時，圍繞桁架結構進行拍攝照片，重建出三維坐標后，依據固定不動的參考點進行坐標對齊，最后計算變形量.當施加一次載荷后，6個觀測點的變形量如圖4所示.監測的結果同時與激光測距儀測量的結果進行對比，其中全站儀的精度為1.0 m m+1.0 p p m.由圖可以看出本文方法與激光測量方法測得的變形趨勢較一致.從而進一步驗證本文方法的有效性.

4 結論

桁架結構的力學性能決定桁架結構的安全性，為了精確地獲取桁架結構的力學性能，本文提出了基于數字攝影測量的桁架結構變形監測方法.詳細討論了標志點識別及三維重建等關鍵技術.為了提高系統精度，提出了基于最小二乘法的捆綁調整算法.最后將本文方法應用于某實際桁架承載變形測量過程，實際結果表明，本文方法可以滿足桁架結構變形監測的精度需求.除此之外，本文方法還具有非接觸、測點多的優點.

〔1〕于承新,全景,李福柱，等.近景攝影觀測鋼結構撓度變形的實驗研究[J].山東建筑工程學院學報,2000,26(2):31-42.

〔2〕馮文灝.近景攝影測量[M].武漢大學出版社,2002.125-130.

〔3〕邾繼貴,葉聲華.基于近景數字攝影的坐標精密測量關鍵技術研究[J].計量學報,2005,26(3):207-211.

〔4〕J.Canny.A computationalapproach to edge detection.IEEE Transactions on Pattern Analysis and machine Intelligence.PAMI-8(Vol.6):679-698(1986).

T U 3 7 5.5

A

1673-260X（2010）10-0105-03