基于N次諧波法的供油凸輪型線的擬合

柴保明,張 浩,高維金,高學攀,谷興海

(河北工程大學機電學院,河北邯鄲056038)

柴油機供油泵主要依靠凸輪軸將高壓燃油輸送到各缸燃燒室,因此作為噴油系統中的重要零件之一,供油凸輪的輪廓形狀直接決定著噴油規律的變化。針對凸輪型線的優化設計,通常采用多項式法、樣條函數法等擬合的方法構造升程函數,來代替供油凸輪升程曲線進行理論分析[1]。

1 諧波法擬合凸輪型線的原理

凸輪升程函數s(φ)只要有適當的光滑性,就能得到對應凸輪轉角 φ的一系列節點(φ0,φ1,…)的凸輪升程數據。根據傅里葉級數展開和收斂定理,s(φ)可在[-π,π] 區間上展開為傅里葉級數[6]

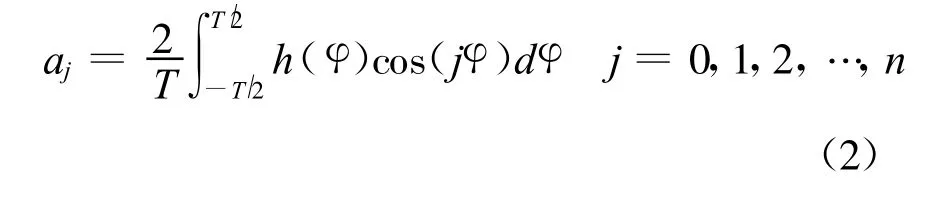
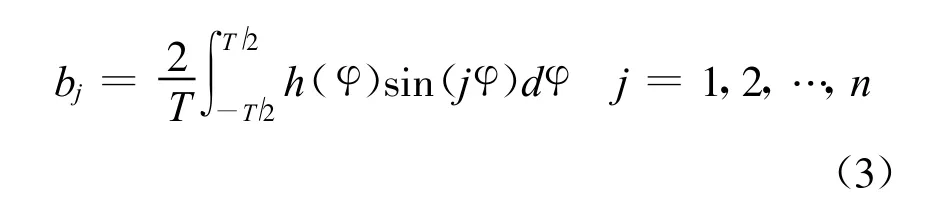
當j∈[1,n] 時,由式(1)得

若滿足|Sn(φ)-s(φ)|＜ε,則可以近似認為Sn(φ)即為所求的升程函數s(φ)。當n增大時,擬合精度提高,當n→ ∞時,Sn(φ)=S(φ)。

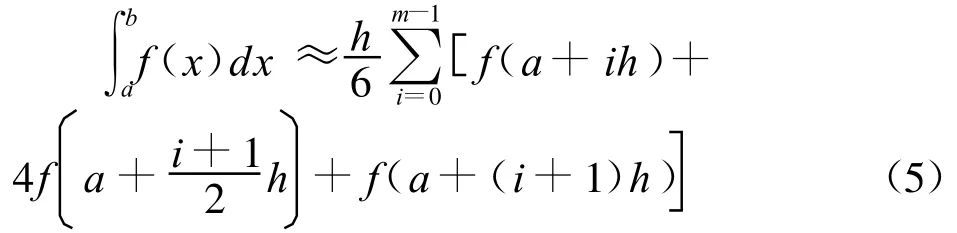
2 凸輪型線擬合

采用N次諧波函數對電控單體集成泵的凸輪型線進行了曲線擬合,凸輪升程按凸輪升程表[7]中所列的間隔提供,控制范圍0°～ 180°,凸輪型線的基本參數如下:凸輪基圓直徑為Dt=34mm,凸輪寬度=18mm,滾輪直徑=22mm,滾輪寬度=17.5mm,最大升程h=12mm,對應的凸輪轉角為63°,并通過MATLAB軟件編程實現擬合如圖1所示。

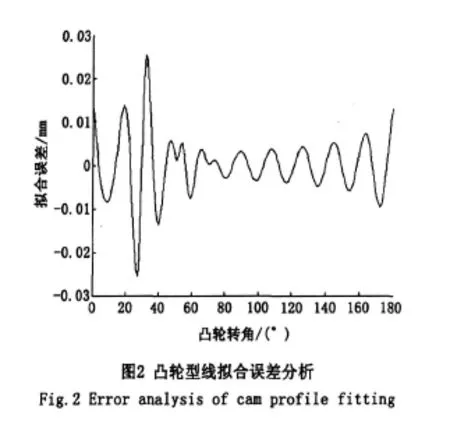
圖2為擬合誤差結果,除少數幾個點之外,其他點都在誤差允許范圍內。原因可能是N的取值有限,出現了截斷誤差。雖然理論上項數N越大,精度越高,但由于在求解的過程中,需要采用數值積分方法近似求解,因此隨著N的增大,積分的誤差會增大,導致擬合結果與實際曲線的誤差增大;另外升程表的取值也是誤差出現的一個重要原因。

3 供油凸輪性能分析

為了便于研究該類凸輪機構運動規律的共同特性,我們把輸入量角度 φ,位移 h、速度 v、加速度a等運動參量進行無因次處理,同時用大寫字母表示這些無因次量[7]。

從數學理論的角度出發,只要滿足狄氏條件,任何曲線均能展開成傅里葉級數的形式,故供油凸輪的滾輪體的速度、加速度、躍度分別可表示為

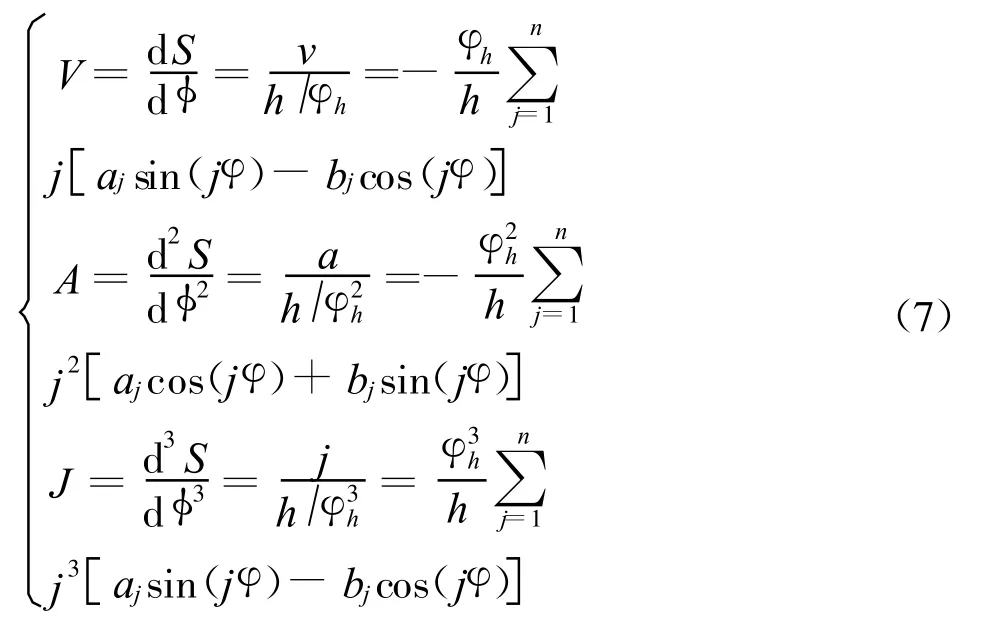
利用MATLAB軟件對位移h、速度v、加速度a的變化規律進行擬合,由圖3可以看出,當凸輪參照轉速為1 500rpm、凸輪轉角為33°時,速度達到最大值;在上升期,等速度區段較大,即凸輪工作段比較大,此時,速度上升比較平穩,循環噴油量比較穩定,同時加速度最大值也在一定的范圍之內;在下降期加速度變化較小,從動件運行平穩、沖擊小。

4 結論

1)N次諧波法對凸輪型線所規定的速度和加速度實現了定量控制,可以計算出準確的諧波函數供油凸輪型線。

2)凸輪升程表的間隔角度影響著N的取值,擬合過程中N的取值受限是造成截斷誤差的主要原因,因此可以適當地增大N值來獲得較高的擬合精度。

3)MATLAB軟件編程實現了凸輪型線擬合,可以直觀的看出凸輪機構運動規律和特性,從而為凸輪優化提供了理論依據。

[1] 李友鋒.N次諧波法擬合供油凸輪型線的討論[J] .內燃機車,2006(4):15-17.

[2] 繆雪龍,張毅華.數值計算在凸輪型線分析中的應用[J] .內燃機燃油噴射和控制,2000(1):17-18.

[3] 吳勤.噴油泵凸輪型線的擬合[J] .拖拉機與農用運輸車,2001(3):26-27.

[4] 嚴國建,劉永長,胡繼澤.諧波函數供油凸輪速度特性的研究[J] .內燃機學報,1992(1):36-40.

[5] 石永剛,吳洋芳.凸輪機構設計與應用創新[M] .北京:機械工業出版社,2007.

[6] 楊東明.凸輪機構反求設計、誤差分析與檢測方法的研究[D] .昆明:昆明理工大學,2002.

[7] 葛正浩,丁英杰,徐峰.平面凸輪精密測量及運動規律反求設計新方法[J] .機械設計與研究,2008(1):32-35.