關聯維數在尾水管壓力脈動分析中的應用

王利英,趙衛國,黃欣鋒

(1.河北工程大學水電學院,河北邯鄲056021;2.邯鄲市水利局漳滏河灌溉供水管理處,河北邯鄲056001)

水輪機尾水管的壓力脈動是影響水輪機穩定運行的主要因素[1-2]。在水輪機運行過程中,利用各種動態測試儀器拾取、記錄和分析水輪機尾水管的壓力脈動信號,可以實現水輪機運行穩定性的控制。毛漢領等[3]對模型水輪機進行了試驗研究,分析了尾水管內部不同位置不同工況下壓力脈動變化規律,為改善尾水管設計提供了參考;也有一些學者在將人工神經網絡應用于建立水輪機數學模型方面進行了研究[4-6],趙林明教授[7]采用人工神經網絡方法分別建立了水輪機特征參數與空化系數的數學模型,水輪機開度與出力的數學模型,以及水輪機特征參數與壓力脈動幅值的數學模型。然而水輪機尾水管中的水力振動信號是隨機信號,其中許多是非線性的無規則的信號,僅憑儀表檢測或工作人員的個人經驗是無法獲取的,因此也就很難準確的掌握水輪機的運行情況。為了準確的掌握水輪機運行時壓力脈動變化規律,選擇一種先進的水力振動類型診斷技術方法是很有必要的。

分形維數是描述復雜系統混沌現象的重要參數,其中其良好特征性的分形關聯維數通過相空間重構和非線性問題建立聯系。本文試圖利用分形關聯維數對水輪機的壓力脈動進行分析,為實現水輪機尾水管壓力脈動狀態的自動識別提供參考。

1 關聯維數基本原理及計算方法[3-5]

1.1 時間序列的相空間重構

在時間序列的分析中,決定序列的可觀測因素很多,而且相互作用的動力學方程往往是非線性的,甚至是混沌的;另外,由于測量精度的實際限制、計算的復雜性,以及可能存在的本質上的非確定性因素等多方面的困難,嚴重地制約了人們對時間序列內在機制的理解。20世紀80年代以來,由于Takens對Whitney早期在拓撲學方面工作的發展,使得深入分析時間序列的背景和動力機制成為可能,在確定性基礎上對序列動力學因素的分析,目前廣泛采用的是延遲坐標狀態空間重構法,一般來說,非線性系統的相空間可能維數很高,甚至無窮,但在大多數情況下維數未知。在實際問題中,對于給定的時間序列x1,x2,x3,…,我們通常是將其擴展到三維甚至更高維的空間中去,以便把時間序列中蘊藏的信息充分地展露出來,這就是延遲坐標狀態空間重構法。

相空間重構的基本思想是,動力系統中任一分量的演化都是由與之相互作用的其它分量來決定的,這些相關分量的信息就隱含在任一分量的發展過程中。

重構相空間過程如下:

對一單變量時間序列{x(i),i=1,2,3…N},對其用延遲時間法進行相空間重構。嵌入維數為m時的相空間向量表示為

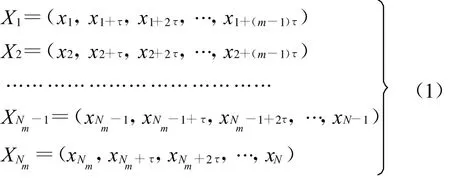
建立重構相空間X

式中m—嵌入空間的維數;n—時間序列信號的數據個數;τ—固定時間間隔,是采樣時間間隔 Δ t的整數倍。

1.2 關聯維數的求解

采用P.Grass Berger與I.Procaccia提出的GP算法,步驟如下:

將時間序列{x(i),i=1,2,3…N進行相空間重構,如式(1)和式(2)。然后定義關聯積分函數。

式中 ε—觀測尺度;θ(ε)—Heaviside函數;γij指從N個點中任選一個參考點xi,計算其余各點到 xi的距離。

對所有的 xi(i=1,2,…,Nm)重復該過程,得到所有點對距離后,計算 C(ε)。關聯積分函數的含義即對于變量ε一定時,對重構相空間xi中的所有點對之間距離小于ε的點個數占所有點的多少。當ε取一定范圍時,關聯積分函數有下式成立

因此,定義關聯維數

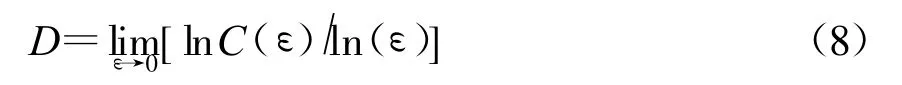
運算時所選定的相空間維數m應當使得ε→0時關聯維數D的值達到穩定狀態,這時即為所求信號的關聯維數。

2 水輪機機組測試

2.1 背景介紹

黃壁莊水庫位于滹沱河出山口處的獲鹿縣黃壁莊鎮馬鞍山兩側,總庫容1.21×1010m3,主壩高128.5m,副壩高 129m,電站裝機 2臺,分別為16 000kW和800kW。水輪機型號:ZZ-LH-465;額定水頭:14.5m;額定流量:120m3;額定輸出功率:16MW;發電機型號:TS-700/81-48;額定功率:16MW。

2.2 水壓脈動測點布置

對于水輪機壓力脈動測點位置的選擇,應使得測點處測得的壓力脈動幅值比其它位置處大;對于因尾水管渦帶引起的壓力脈動,其水輪機最大脈動值一般出現在尾水管錐管(0.3-1.0)D2處[6-7]。因此,測試時將尾水管水壓力脈動測點布置在尾水管進入門處,并從尾水管錐管段鋼板管壁處用長500mm的4#普通自來水管引出至水壓脈動傳感器。壓力脈動傳感器安裝時,注意應與流道齊平,且不能與其它管道連通或窩氣,不允許在測點處與傳感器之間用管路連接,以避免連接管對實際信號的緩沖、衰減或共振,影響幅頻特性和相位特性的準確測量。圖1為水壓脈動測點布置圖。

2.3 試驗結果

待工況穩定后進行采樣,采樣時間20s,采樣頻率1 500Hz。共進行了25個工況采樣,見表1。

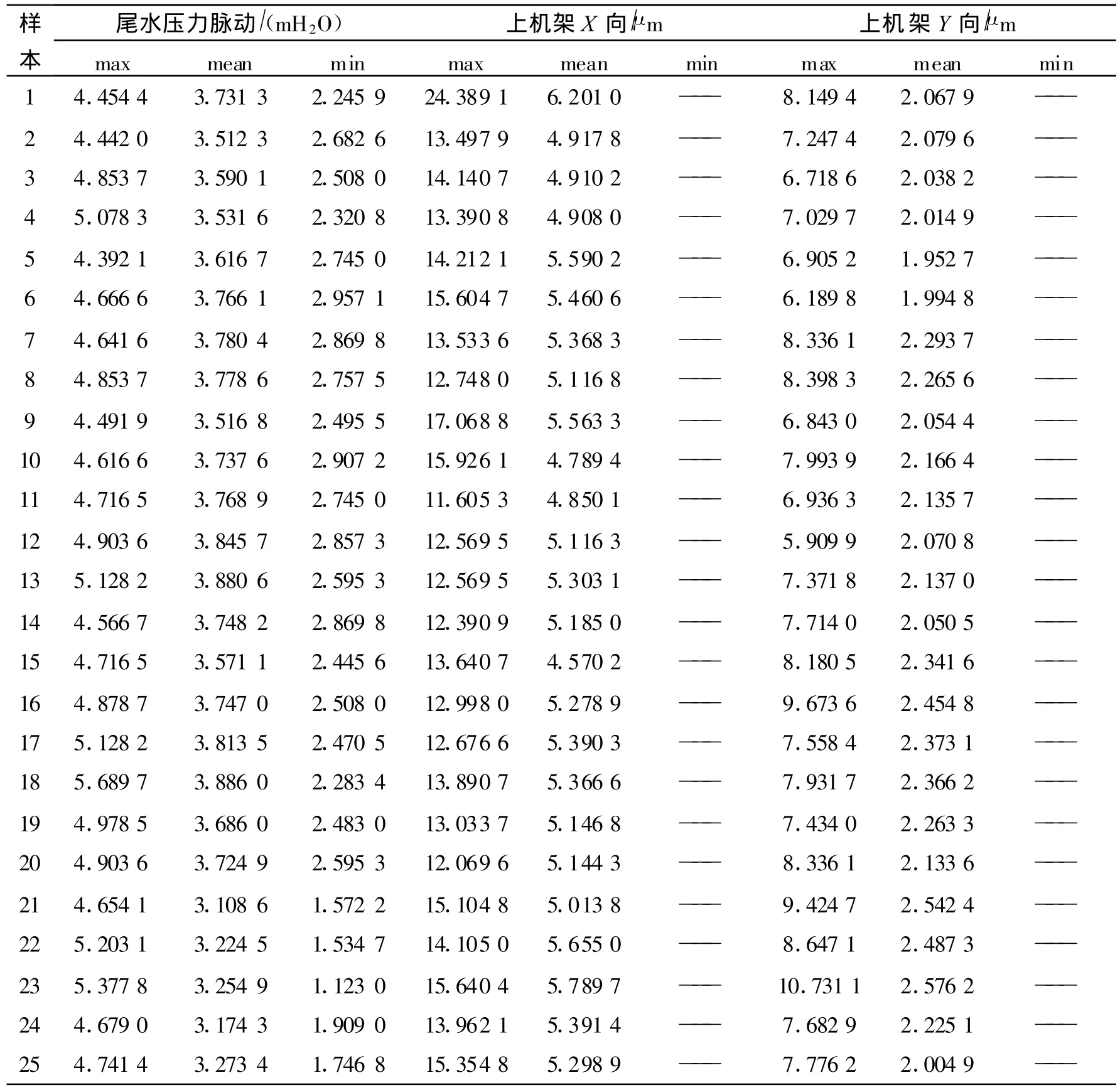
表1 采樣工況Tab.1 Working condition of sampling

采用東方所信號處理軟件對測點采集信號進行頻域分析(圖 2)。時域指標統計:最大值為0.046mm,峰峰值為 0.083 43mm,有效值為0.018 8mm。時域統計結果:最大值為0.033 9mm,峰峰值為0.073 54mm,有效值為0.018 1mm。由測試軟件分析結果可知機組測量部位的振動值無嚴重超標情況。

3 關聯維數在尾水管壓力脈動中的應用

將隨機挑選得到的尾水管壓力脈動測試值作為試驗數據,進行工況測試。本實驗選用的是水輪機漿葉開度為50.70%和導葉開度為62.85%時相對應的測試值,所有的試驗數據都經過電子濾波器濾波處理后直接采集,因此數據信號的降噪問題已經解決。

3.1 采樣長度的選取[8-9]

在選取采樣長度N時,除根據上述理論要求進行選取外,為了保證數據的穩定性和可靠性,截取壓力脈動值中間的一部分數據作為關聯維數計算方法中的單變量時間序列 xi(i=1,2,…,Nm),以避免測試起始和終止時測試儀器對測試數據所帶來的穩定性影響。由于不同的時間序列長度,計算所得分形關聯維數略有不同,但隨著時間序列長度的增大,分形關聯維數趨于穩定,同時也為了保證選取的采樣長度能夠體現尾水管的壓力脈動特性,選取512個振動試驗數據作為研究對象,即N=512。

3.2 嵌入維數的選取

嵌入維數 m是重構相空間的一個重要參數[10],m的確定是關聯維數計算的重要前提。通過逐漸增大m,直至關聯維數的值不再變化時,即可求出最小的嵌入維數。

3.3 時間延遲的選取

由公式(8)可得時間延遲τ=14s。

3.4 結果與分析

根據前面試驗參數,通過對測試數據進行分析,數據計算結果如表2所示。

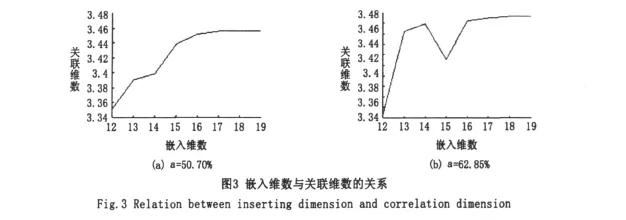
根據表2,繪出了導葉開度 a為50.70%和62.85%時的嵌入維數與關聯維數的關系圖(圖3)。當嵌入維數是大于等于18時,關聯維數為定值分別為3.456 6和3.388 1。即關聯維數曲線的無標度區線性較好,關聯維數趨于穩定值,因此最小嵌入維數取18,它表征了動力系統有效自由度數目。

表2 實測信號的關聯維數Tab.2 Correlation dimension of actual signal

根據表1的數據,得到了相應工況下水輪機尾水管壓力脈動的測試結果如圖4所示,可以看出不同開度下尾水管壓力脈動的振幅不同。由圖5可以得到導葉開度為50.70%和62.85%時其分形關聯維數分別為3.456 6和3.388 1,與表2所得結果吻合。由此可以得出不同工況下水輪機尾水管壓力脈動的關聯維數也是不同的,因此,關聯維數可以作為判斷尾水管壓力脈動的指標。

4 結論

1)當嵌入維數大于等于18時,關聯維數趨于穩定值。

2)不同工況下水輪機尾水管壓力脈動的關聯維數也不同,當導葉開度為50.70%時,分形關聯維數為3.456 6;導葉開度為62.85%時,分形關聯維數為3.388 1。

3)關聯維數可以作為對水輪機尾水管壓力脈動情況進行識別的指標,可以指導電站的穩定運行。

[1] 王珂侖.水力機組振動[M] .北京:水利水電出版社,1986.

[2] 何成連,王正偉,丘華.水輪機尾水管內部壓力脈動試驗研究[J] .機械工業學報,2002,38(11):62-65.

[3] 毛漢領,熊煥庭,沈煒良.偏相干分析在水電站振動傳遞路徑識別的應用[J] .廣西大學學報(自然科學版),1998,23(1):6-9.

[4] HUI W,QINGYU P,ZHANG ZHI C,et al.Vibration analysis of elastic plate submerged in incompressible viscous fluid by copuling finite element method[J] .ACTA Mechanical Solida Sinica,1998(11):1-12.

[5] 劉玉民,孫開朗,張帆,等.水輪機發電機組動力穩定性研究[J] .哈爾濱工業大學學報,1998,30(增刊):82-84.

[6] 趙林明.人工神經網絡的虛擬輸入方法及其在水輪機建模中的應用[J] .華北水利水電學報,1995,16(2):62-66.

[7] 陳予恕.非線性振動[M] .北京:高等教育出版社,2002.

[8] 趙林明,呂為亮,張貴棉.考慮水力振動特性求取轉槳式水輪機的協聯關系[J] .河北工程大學學報(自然科學版),2007,24(4):74-75.

[9] 楊江天,陳家驥.時間序列關聯維數在非線性系統運動性態識別中的應用[J] .航天學報,2003,24(1):28-30.

[10] ANGELO C.Parallel computation of the correlation dimension from a time series[J] .Parallel Computing,1999,25(6):639-666.

[11] 潘羅平.水輪機壓力脈動試驗方法的研究[J] .水力發電學報,2003(3):107-113.

[12] 何成連,王正偉,丘 華.水輪機尾水管內部壓力脈動試驗研究[J] .機械工業學報,2002,38(11):62-65.

[13] WOLF A,SWIFT J B,SWINNEY H L,et al.Determining lyapunov exponents from a time series[J] .Physica D:Nonlinear Phenomena,1985,16(3):285-317.

[14] 張安兵,張俊芳,李喜盼,等.煤礦井筒變形混沌特征分析[J] .河北工程大學學報(自然科學版),2009,26(3):85-88.

[15] 萬書亭,李和明,李永剛.發電機繞組故障時振動的關聯維數分析及診斷[J] .振動、測試與診斷,2005,25(3):210-213.