一維常系數對流方程的步長定律和固有差分格式
李 娟
(北京理工大學機電學院,北京100081)
一維常系數對流方程的步長定律和固有差分格式
李 娟
(北京理工大學機電學院,北京100081)
由常用差分格式得出的差分余項中的奇數次冪項和偶數次冪項分別會產生彌散(色散或頻散)和耗散效應。但是利用泰勒展開式并且使差分余項為零,可以得出一維常系數對流方程的步長定律和固有差分格式,結論也適用于解類似的變系數雙曲型方程和擬線性雙曲型方程。
偏微分方程;雙曲型方程;對流方程;數值解法;差分格式
雙曲型方程的一些常用數值解差分格式得出的差分方程會有差分余項存在,因此差分格式計算出的數值解有誤差。雖然可以采用更復雜、精度更高的差分格式來降低誤差,但是這樣仍然存在計算量大和誤差這兩個問題,所以有必要尋求完全表示原微分方程的差分方程。通過利用泰勒(Taylor)級數展開[1],并且促使差分余項為零,可以解決因差分余項引起的彌散(色散或頻散)和耗散效應,使數值解與解析解保持一致。
1 Lax-Friedrichs差分格式的泰勒(Taylor)級數展開
一維常系數對流方程:

其中u=u(x,t),a為常數且不為零。Lax-Friedrichs差分格式[2]:

其中,τ為時間步長,h為空間步長。即得:

設u=u(x,t)是原微分方程(1)的光滑解,并且都在u(xi,tn)處由泰勒級數展開得:

將上述三式代入(2)式中,并整理得:

2 差分余項的消除
由原微分方程(1)得:

將(4)式代入(3)中,并整理得:


R(xi,tn)即為差分余項。當a2τ2-h2=0時,R(xi,tn)=0,那么由差分方程(2)式得到的微分方程(5)等價于原微分方程(1)。分別將aτ=h和aτ=-h代入(2)式中得:當aτ=h時,=;當aτ=-h時,。實際上,也可以通過采用這種方法對迎風格式(upwind)、Lax-Wendroff格式和Beam-Warming格式進行分析從而得出相同的結果。
3 結論
一維常系數對流方程的固有差分格式:

對于?u/?t+a(x,t)?u/?x=0這樣的變系數雙曲型方程,雖然特征線dx/dt=a(x,t)是一條曲線,但是u的值沿特征曲線保持不變,所以若已知a(x,t),那么將同一條特征線上相鄰兩時刻點的相對斜率(△x/△t)作為當前步長內的常數a值,在每步內看作常系數雙曲型方程,這樣計算出的值即為準確解。對于?u/?t+u?u/?x=0這樣的擬線性雙曲型方程,滿足a=u0,即由初值確定常數a的一系列不同的一維對流方程,每一點仍可用常系數對流方程來解。
4 應用
例 設方程

滿足邊界條件:u(1,t)=u(111,t)=0和初始條件:

解 選取τ=h=a=1,依據一維常系數對流方程的固有差分格式得t=0、t=43和t=86時x軸上各點的u值分別如圖1、圖2和圖3所示。

圖1 t=0時各點的u值
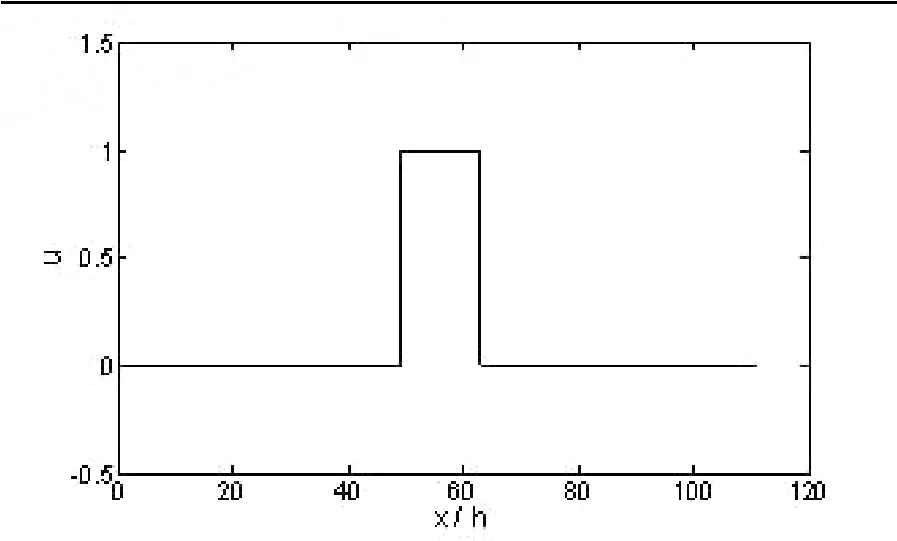
圖2 t=43時各點的u值

圖3 t=86時各點的u值
5 總結
本文得出一維常系數對流方程數值解法的步長定律和固有差分格式,解決了其他差分格式因差分余項帶來的誤差,結果對于解類似的簡單變系數雙曲型方程和擬線性雙曲型方程也適用。實際上,差分方程穩定與不穩定的邊界就是原微分方程。
[1] 惲壽榕,涂候杰,梁德壽,等.爆炸力學計算方法[M].北京:北京理工大學出版社,1995:63-65.
[2] 陸金甫,關治.偏微分方程數值解法[M].2版.北京:清華大學出版社,2004:45-54.
O241.82
A
1671-2544(2010)03-0029-02
2010-03-03
李 娟(1984— ),男,湖北廣水人,北京理工大學機電學院碩士研究生。

