蟻群算法在車間調度問題中的應用

張曉玲，何彩香，陳建華

（大理學院數學與計算機學院，云南大理 671003）

蟻群算法在車間調度問題中的應用

張曉玲，何彩香，陳建華

（大理學院數學與計算機學院，云南大理 671003）

提出用蟻群算法求解車間調度問題。車間調度問題是典型的非確定性多項式時間難問題，蟻群算法是一種分布式進化計算方法，具有魯棒性，正反饋，并行性等特點，而且算法簡單。給出了用蟻群算法求解車間調度問題的流程，并且用經典的J SP的樣例對算法進行了測試，實驗結果表明用蟻群算法可以求解得到車間調度問題的最優解或近似最優解。

蟻群算法；車間調度問題；信息素；

0 引言

車間調度問題（Job-Shop Scheduling Problem，JSP）是在經典的調度理論中所描述的最難的組合問題中的一種，是典型的非確定性多項式時間難問題（NP）。已經有許多方法用來解決JSP，包括線性規劃、神經網絡〔1〕、遺傳算法〔2〕、禁忌搜索〔3〕、粒子群算法〔4〕和螞蟻系統等等。

蟻群算法（Ant Colony Algorithm，ACA）是由意大利學者M.Dorigo在20世紀90年代提出的一種模仿自然界螞蟻群的覓食行為的一種分布式進化計算方法，具有并行性、算法簡單和求解效率高等特點。蟻群算法模擬了自然界螞蟻尋找從蟻巢到食物源的最短路徑并找到回蟻巢路徑的機制，螞蟻之間通過一種信息素（“激發工作”，stigmergy）〔5〕來相互交流信息。螞蟻在移動的過程中，會在經過的路徑上散發信息素，蟻群通過感知路徑上的信息素進行通信，個體之間并不直接進行交互，而是通過改變它們共同存在的環境進行交互，個體又通過對環境的改變去影響其它個體的行為，從而形成了一種正反饋機制。長度越短的路上，經過的螞蟻越多，聚集的信息素也越多，螞蟻趨向于選擇信息素多的路徑移動。通過這種機制，經過一段時間后螞蟻最終能夠發現最短路徑。蟻群算法已經被成功地應用于解決組合優化問題，如：旅行商問題（Traveling Salesman Problem）〔6〕，二次分配問題（Quadratic Assignment Problem），JSP等。本文討論的是用ACA求解JSP。

1 車間調度問題

1.1 問題的描述 JSP問題可以描述為：有n（n≥3）個加工順序不同的工件要在m（m＞2）臺機器上完成加工。

已知：工件集J=｛J1，J2，…，Jn｝，Ji為第i個工件，i= 1，2，…，n；機器集M={M1，M2，…，Mm}，Mj為第j號機器，j=1，2，…，m；每個工件有k道工序，每道工序要求在不同的機器上加工，并且預先已經定義了每個工件在m臺機器上的加工順序，uij表示工件i在機器j上加工，工序序列集O={uij｜i∈〔1，n〕，j∈〔1，m〕｝，其中n為工件的數目，m為機器的數目。

每個工件使用每臺機器的時間矩陣T，tij∈T為第i個工件Ji使用第j臺機器的時間。tij=0表示工件Ji不使用機器Mj。

JSP問題滿足以下約束：①每個工件使用每臺機器不多于1次；②不同的工件的工序之間沒有先后約束；③每臺機器一次只能加工一個工件，并且工序一旦進行不能間斷；④工件加工過程中沒有新工件加入，也不臨時取消工件的加工。

cij=cik+Tij是工序uij相對于關系uik→uij的完整的執行時間，調度目標：求出可行的工序的加工序列，使其最后一道工序的最大完工時間Cmax最小。

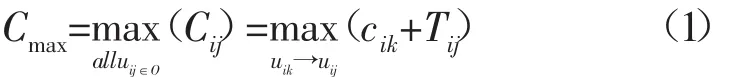
1.2 JSP的表示 可以用析取圖D=（N，A，B）來表示JSP問題，N是所有結點的集合，每個結點對應一個工件的一個工序uij，并且N=m·n。A是工件使用機器的加工順序的有向弧的集合。B是連接在同一臺機器上處理的不同工件工序的無向弧的集合。為了確定先對哪個工件進行加工和什么時候加工結束，需要設置一個初始結點O0和調度結束的結點O10。以3個工件3臺機器的問題作為例子。如圖1。

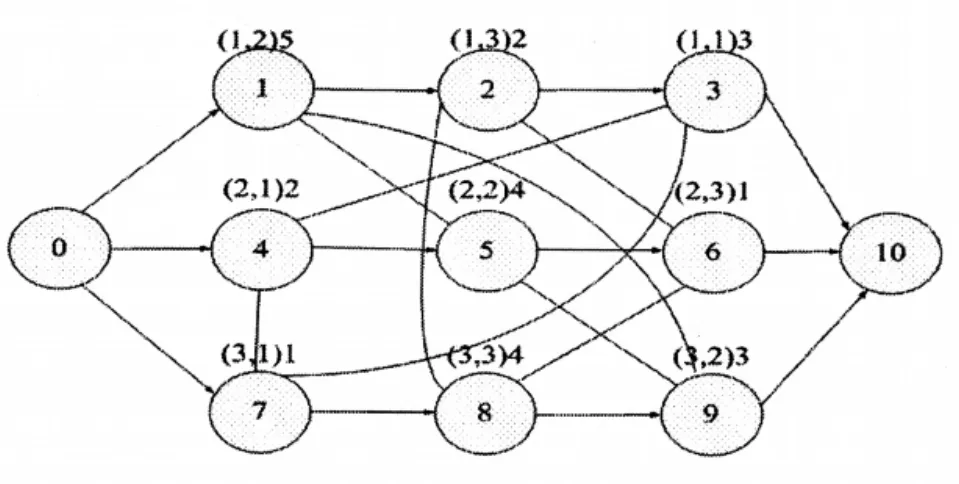
圖1 3／3／G／Cmax JSP的表示圖

在圖1中，0=O0，10=O10，1=u12，2=u13，3= u11，4=u21，5=u22，6=u23，7=u31，8=u33，9=u32，結點1旁邊的（1，2）5表示工件1的第一道工序在機器2上處理，處理時間為5，圖中除與O0和O10相連的有向弧，其它的有向弧表示同一個工件的加工順序，工序必須按照該順序進行加工，其它的為無向弧。每一行加工一個工件，123加工工件1，456加工工件2，789加工工件3。每個工件只能使用每臺機器一次，有m臺機器，則每個工件就有m道工序。因此求解JSP就變成在滿足約束的前提下，求得上圖中結點的一個序列，例如{4，1，7，8，2，3，5，9，6｝，求出在每臺機器上加工完畢所有的工件的最后一道工序時的最大完工時間，求解目標：求出最大完工時間最小的序列，即為調度的最佳序列。

2 ACA求解JSP

根據圖1，ACA求解JSP的基本工作過程如下：

由于在整個工件調度的過程中添加了一個開始的結點O0和結束的結點On+1，因此所有的螞蟻從結點0（工序0）出發，最后到達的結點是結點10。設集合Gk是沒有訪問過的結點的集合，Sk表示根據約束規則下一步允許訪問的結點的集合，還需要一個禁忌表J k，存放已經訪問過的結點。在上面的例子中，Gk={1，2，3，4，5，6，7，8，9}，Sk={1，4，7}。首先螞蟻分布在0結點，然后每個螞蟻根據狀態轉移規則選擇下一個結點，螞蟻傾向于選擇那些加工時間較短且信息素強度較高的路徑，圖中的每個弧表示節點間信息素的量和啟發式距離的一對值 {αij，Tij}，Tij通常為對工件j的第i步工序的加工時間。每選擇一個結點，該結點就被追加到禁忌表Jk中并從Gk中刪除：如果被選的結點不是工件的最后一步，那工件中緊鄰的下一個結點就會被加入到Sk中。單個的螞蟻在遍歷過程中根據信息素局部更新規則在路徑上釋放一定數量的信息素，同時螞蟻經過的路徑上的信息素隨著時間的推移而蒸發。當所有的螞蟻都完成了它們的遍歷過程之后，Gk=?。最后禁忌表中得到的結點的排序序列就是螞蟻k找到的解。此時可以計算出此次迭代的最小的最大完工時間，再應用信息素全局更新規則對獲得最小的最大完工時間的螞蟻所經歷的邊上的信息素進行更新。此后算法反復迭代直至滿足終止條件后結束。可見，蟻群算法的求解過程主要由三個規則控制，即狀態轉移規則，信息素全局更新規則和信息素局部更新規則。下面將對這三個規則進行說明。

2.1 狀態轉移規則 ACA中的狀態轉移規則（又叫做“偽隨機比例規則”），“偽隨機比例規則”為在保持探索（exploration）一條新的邊和利用螞蟻所積累的搜索經驗開發（exploitation）一條邊之間的平衡提供了一種直接的方式，狀態轉移規則如下：位于結點r的螞蟻k使用以下的規則（1）選擇結點s為下一個要訪問的結點

在（2）中，τ是信息素，η是啟發函數，η（s）=1/T（s）是在結點s的工序在機器上的處理時間的倒數，Sk是螞蟻k還沒有訪問過的結點的集合，而β＞0是一個參數，用來定義信息素和時間之間的相對重要性。q是一個均勻分布的隨機數，q∈〔0，1〕，0≤q0≤1是自定義的一個參數。S是根據以下的概率公式（3）計算得來的隨機變量。

偽隨機比例規則使得螞蟻傾向于選擇加工時間短且信息素強度濃的路徑。參數q0決定了“探索”和“開發”之間的相對重要性。當位于結點r的螞蟻k要選擇下一個將要訪問的結點時，它選擇一個隨機數0≤q≤1，如果q≤q0則按照式（1）根據啟發信息和信息素強度取最好的邊，否則，按照式（2）隨機比例規則選擇下一條要移動的邊。

2.2 信息素全局更新規則 在ACA中，當所有的螞蟻都訪問完所有的結點以后，只有那些屬于最小的最大完工時間的邊上的信息素才被得到增強，信息素全局更新規則的使用使算法的尋優過程更具有指導性：最小的最大完工時間尋找始終是在當前找到的最小完工時間的附近進行。按以下的公式（4）對最小的最大完工時間的邊上的信息素進行更新。

其中，

0＜α＜1是信息素衰減系數，而Tgb是螞蟻k在本次循環中找到的最小的最大完工時間。

2.3 信息素局部更新規則 單個的螞蟻在遍歷過程中按照式（5）信息素局部更新規則對它所經過的邊上的信息素進行更新。

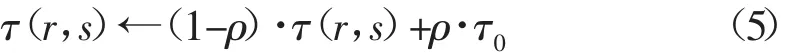
0＜ρ＜1是信息素揮發系數，τ0是預先設置的信息素的初始值，信息素局部更新規則使得被螞蟻經過的路徑減少了一部分信息素，使得這些邊被后來的螞蟻經過的可能性減少，增強了算法的“勘探”能力，從而有效的避免算法進入停滯狀態（所有的螞蟻收斂到同一解）。

2.4 ACA求解JSP的算法描述 假設以下是求n個工件m個機器的JSP問題，螞蟻的個數為工件的個數，則求解JSP的ACA流程圖。見圖2。

描述如下：

步驟1：初始化算法的各項參數：初始信息素τ0，ρ，β，α，螞蟻個數n，最大迭代次數，工件數n，機器數m等等；

步驟2：把n只螞蟻放在開始結點0上；

步驟3：每一只螞蟻應用偽隨機比例規則（2）和（3）選擇下一個要訪問的工序，并應用信息素局部更新規則（5）更新螞蟻所經過的路徑上的信息素；

步驟4：所有的螞蟻都到達了最后結束的結點n+l，每只螞蟻就構建了JSP的一個解，計算出此次迭代中所有螞蟻的最大完工時間，求出其中完工時間最小的值，應用信息素全局更新規則（4）更新最小的最大完工時間的邊上的信息素；

步驟5：判斷是否已經滿足結束的條件，如果滿足，則輸出最小的最大完工時間的值，否則跳轉到步驟2繼續執行下一次的迭代。

3 實驗仿真與結果分析

本文采用了4個經典的JSP問題：FT03，FT06，LA06和LA07的測試用例來說明用ACA求解JSP的優勢。

3.1 實驗仿真 樣例的規模不同，ACA在求解時候的參數的設置也不同，具體的參數設置見表1。

表1 蟻群算法求解JSP的參數設置

為了降低由于系統和統計的誤差，對求解的每個用例都進行了10次的仿真，實驗結果是10次仿真的統計值（平均最優值和方差等）。

3.2 結果比較 表2給出了使用ACA求解4個樣例的結果，由于這里給出的數據是基于10次測試的平均值，因此可能會有小數。同時，表中的“OPT”一列是樣例的已知的最優解。從表2的數據中可以看出，采用ACA來求解JSP具有非常明顯的優勢。ACA能夠很快的找到問題的最優解。為了能更加直觀地反映算法的優勢，圖3給出了FT06，LA06和ABZ6在優化問題的時候的進化特征曲線。

表2 基于表1的參數設置的ACA求同JSP的平均結果

圖3 ACA求解不同JSP的進化特征曲線圖

在圖3中可以看出ACA在求解JSP（FT06，LA06和AB Z6）時用了1 000次迭代的收斂速度，一般都在500次迭代左右就可以收斂（ABZ6問題的最優解出現在每次迭代中）。雖然表2和圖3都體現出了A C A在求解J S P時的高效性，當然A C A在求解JSP時也存在工件數目越多算法的時間復雜度越大等問題。

對于ACA求解復雜的J S P的時間消耗，還需要對A C A進行改進或融入其它的一些算法，以使算法能夠在求得最優解的基礎上時間消耗最小。

4 結束語

針對ACA求解JSP，對該算法的基本原理進行了闡述并且給出了具體的實現方案，最后還通過典型的JSP測試樣例進行實驗仿真，實驗結果證明了該策略不但在收斂速度上而且在求解精度上都有很大的優勢。

〔1〕唐大志.用Hopfield神經net解決作業調度問題〔J〕.遼寧工程技術大學學報，2004，23（S）：88-90.

〔2〕李勝輝，李瑩.遺傳算法與人工免疫算法對車間調度問題求解〔J〕.計算機應用研究，2009，26（8）：2928-2930.

〔3〕李俊清，潘全科，王玉亭，等.塊鄰域結構的禁忌搜索算法在車間調度問題中的應用〔J〕.機床與液壓，2009，32（11）：173-188.

〔4〕張長勝，孫吉貴，歐陽丹彤，等.求解車間調度問題的自適應混合粒子群算法〔J〕.計算機學報，2009，32（11）：2138-2145.

〔5〕Dorigo M，Stitzle T.Ant Colony Optimization〔M〕.MA：MITPress，2004.

〔6〕張曉玲，黃力.融入遺傳算子的蟻群算法求解TSP問題〔J〕.廣西民族大學學報，2009，15（3）：81-87.

Ant Colony Algorithm for Solving Job-Shop Scheduling Problem

ZHANG Xiaoling,HE Caixiang,CHEN Jianhua
（College ofMathematics and Computer Science，DaliUniversity,Dali,Yunnan 671003,China）

This paper proposes Ant Colony Algorithm（ACA）to solve Job-shop Scheduling Problem（JSP）.Job-Shop scheduling problem is a typical NP hard problems,ant colony algorithm is a distributed evolutionary computation methods,The main characteristics of this algorithm are robustness,positive feedback,parallelism,and simple.In this paper,the flow of ant colony algorithm used to solve Job-shop scheduling problem is given,the numerical experiments of ACA were implemented in a small JSP, the experimental results show that the ant colony algorithm can be used to solve job shop scheduling problem and the optimal solution or near optimal solution can be achieved.

Ant Colony Algorithm;Job-Shop Scheduling Problem;pheromone;

TP18

A

1672-2345（2010）10-0010-05

云南省教育廳科研基金資助項目（2010Y349）

2010-04-09

2010-05-20

張曉玲，講師，主要從事進化計算的研究.

（責任編輯 董 杰）